顺序表
顺序表
如果你不想看
- 顺序表在物理上是连续的。
- 尽早进行测试会使你查错的难度大大降低。
- 插入数据和删除数据时,都需要对后面的元素进行移动。
- 移动要注意方向,防止覆盖有效数据。
- 测试你的边界。
顺序表的定义
如果物理实现上也将线性表的元素依次存放,也就是说在物理上是连续的,那就形成顺序表。
我们可以用以下的代码来展示顺序表的ADT[1]:
struct SEQUENCE{
SEQUENCE( int size=10 ); // 初始化
~SEQUENCE(); // 销毁
void append( int value ); // 在最后插入值value
void insert( int index, int value ); // 在第index位插入value
void remove( int index ); // 删除第index位的元素
int& get( int index ); // 获取第index位元素
int search( int value ); // 搜索值等于value的元素,返回其对应的index
void show() const; // 打印顺序表的所有内容
};
这里我们给SEQUENCE( int size )这个构造函数设置了初始化的参数size。因为从具体的实现上,顺序表的内存空间是很难快速增补的。对于这样的构造,我们通常会预留一部分空间,避免出现空间不够用的情况,这里的size就是预留的空间尺寸。
对于SEQUENCE这个结构体,我们已经定义了它所应该包含的方法(成员函数)。现在我们需要想想,要实现这些方法,我们需要定义那些属性(成员变量)[2][3]。
比较容易想到的,我们会在初始化的时候,分配一个空间用于存放数据,所以我们会需要一个指针来指向这个存放的空间。 其次因为我们预留了一定的空间,那么也需要记录下来,可以用来判断空间是否满。 最后我们会需要一个变量来记录当前元素数量(注意和上一个变量区别)。
于是我们给出了完整的定义:
struct SEQUENCE{
int* data=nullptr;
int size=0;
int count=0;
SEQUENCE( int size=10 ); // 初始化
~SEQUENCE(); // 销毁
void append( int value ); // 在最后插入值value
void insert( int index, int value ); // 在第index位插入value
void remove( int index ); // 删除第index位的元素
int& get( int index ); // 获取第index位元素
int search( int value ); // 搜索值等于value的元素,返回其对应的index
void show() const; // 打印顺序表的所有内容
};
这里的定义int *data=nullptr是C++的新特性,作用是设置data这个属性的默认值,这样所有SEQUENCE实例化的所有对象中的data属性都会设置成nullptr(空指针)。
初始化和销毁
我们用构造函数和析构函数来初始化和销毁对象:
SEQUENCE::SEQUENCE( int size ){
data = new int [size];
this->size = size;
count = 0; // 开始时元素为0个
}
SEQUENCE::~SEQUENCE(){
if(data){
delete[] data;
data = nullptr; // 将指针置空,防止野指针问题
size = 0;
count = 0; // 参数最好恢复原值
}
}
这里需要注意的是我们销毁对象时的操作。我们只需要执行delete[] data即可。但我们增加了条件判断,保证在data==nullptr时不会执行销毁操作。同时剩下的三条语句可以将对象恢复初始状态,尤其是将指针data置空这个操作,可以防止误访问已释放指针导致的问题[4]。
请注意良好的编码风格,可以很大程度上降低编码的难度。
要测试吗?
要!
你可能认为这点代码毫无测试的必要,但越是经验丰富的程序员,会越频繁地进行测试。 即便这点代码,也可以进行测试。 这时我们会发现由于析构函数只能在元素销毁时被调用,我们是很难测试析构函数的。 为了达到充分测试,我们需要一些技巧: 第一种方法是利用你的调试器,断在析构函数里,这样通过调试器你可以看到你代码执行的结果。 第二种方法可以用变通的办法来处理:
struct SEQUENCE{
// ...
// 增加一个destroy函数用来执行真正的销毁
void destroy();
~SEQUENCE(); // 销毁
};
void SEQUENCE::destroy(){
if(data){
delete[] data;
data = nullptr; // 将指针置空,防止野指针问题
size = 0;
count = 0; // 参数最好恢复原值
}
}
SEQUENCE::~SEQUENCE(){
if( data ){
destroy();
}
}
这样我们可以直接测试destroy函数,这种方式有利于自动化测试框架的实施:
int main()
{
// 通过打印初始化后和销毁后data指针的值来测试两个构造和销毁是否正确
SEQUENCE seq;
cout << ((long long)(seq.data)) << endl;
seq.destroy();
cout << ((long long)(seq.data)) << endl;
return 0;
}
无论选哪种方式,尽早、全面地进行测试,出现问题时排错的效率才会更高。
元素添加和打印
尽早实现打印函数有助于我们后续功能的测试。但在打印之前表里必须有数据才行,所以我们先编写append函数,将数据插入表的最后。
void SEQUENCE::append( int value ){
data[count++] = value;
}
这里的逻辑很容易理解。count表明当前的表里有几个数据,实际上也是下一个要被写入的空间的位置。
回忆一下下标和尺寸的关系
如果对此理解不能,你需要多写一些数组的代码。
在熟练掌握这点之后,你会发现我们习惯使用的前开后闭区间([begin, end))非常合理。
要测试吗?
一行的代码也有测试的必要吗?有!如果你没把握的话。
举例来说,如果你误写成data[++count] = value; 直接调用你写的show函数打印出来的结果就会不正确。
那么此时你怎么知道问题是append函数,还是show函数的呢?
至于如何测试,相信你应该不难写出对应的测试代码。当然用调试器也是可以的。
然后我们编写show函数来打印所有数据,注意我们使用的前开后闭区间([0, count))
void SEQUENCE::show() const{
for( int i=0; i<count; ++i ){
cout << data[i] << " ";
}
cout << endl;
}
之后我们用下面的代码来直接测试:
int main()
{
SEQUENCE seq;
seq.append(1);
seq.append(2);
seq.append(3);
seq.show();
return 0;
}
显然我们应该得到:
1 2 3
元素插入
除了在顺序表的尾部插入元素之外,还有一种操作是需要在任意位置插入元素。

对于这种要求,难度显然要高于直接在后面添加。 我们面对的最大的问题是其中并没有空位。这也比较好解决,就像你插队一样,让后面的人让一让就可以了:
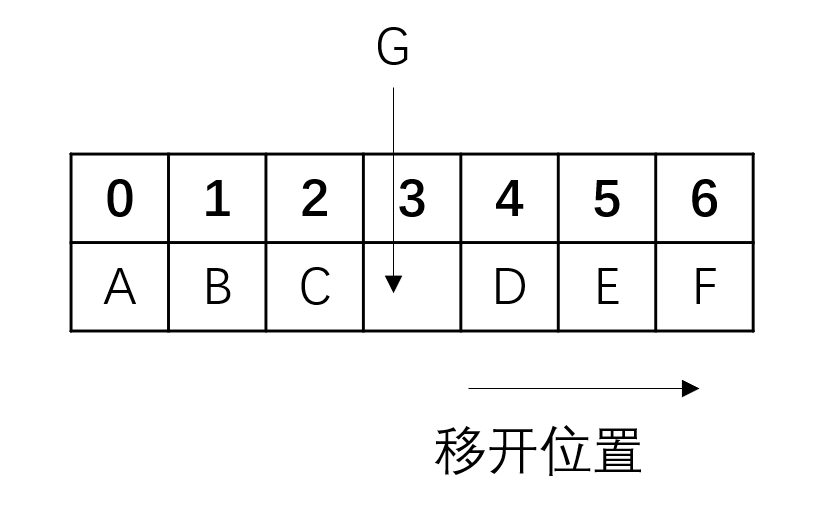
所以我们可以写下这样的代码:
void SEQUENCE::insert(int index, int value){
for( int i=index; i<count; ++i ){
data[i+1] = data[i];
}
data[index] = value;
}
然后测试:
int main()
{
SEQUENCE seq;
seq.append(1);
seq.append(2);
seq.append(3);
seq.append(4);
seq.show();
seq.insert(1,5);
seq.show();
return 0;
}
从这里可以看出为什么要先写show函数和append函数——可以帮我们构造测试环境,为后面的函数增加便利。
提示
先写对你测试有帮助的函数! 先构造测试环境,再完善你的代码!
我们预期的结果应该是1 5 2 3 4,让我们跑一下:
1 2 3 4
1 5 2 2
很遗憾,这次不对。如果你仔细思考,你很容易发现一个问题:数目不对。 插入一个元素之后,元素的数目应该增加,所以我们漏了一句count++:
void SEQUENCE::insert(int index, int value){
for( int i=index; i<count; ++i ){
data[i+1] = data[i];
}
count ++;
data[index] = value;
}
但这样依然不对:
1 2 3 4
1 5 2 2 2
这里的问题,是很容易可以通过调试发现的。我们预计的操作,第一轮将下标是1的2向后移动一位,接下去我们预期是将下标是2的3向后移动一位。
但当你仔细调试时,你会发现下标2的元素此时值是2,不是3。
再结合后面的数字都是2的情况,你应该很容易推断出问题的原因: 我们将2向后移动一位的时候,就将原来是3的位置覆盖成2了。 接下来每一步我们都在将这个2向后覆盖。 所以5后面的数字全变成了2。
让代码跑起来
我希望这个例子可以告诉大家一个很浅显的道理: 抄起键盘就写代码确实是一种不好的习惯,但也没什么。 代码跑出问题,也不可怕。 一旦你构造合适的测试环境,并切实地让你的代码跑起来,你就可以发现你逻辑中隐藏的问题你。 一旦你做了针对性的调试,并仔细地分析情况,错误总可以被解决。 尤其对这种必然出现的错误。
最大的错误是不让你的代码跑起来。
明白了错误的原因,我们就知道要如何处理了。元素移动的次序必须从后向前,而不是从前向后。
请注意是移动元素的次序,而不是元素移动的方向。
你可以想象最后一位的后一位有一个空位,我们必须把这个空位一步步地向前移动,移动到我们要插入的位置,所以正确的代码应该是:
void SEQUENCE::insert(int index, int value){
for( int i=count-1; i>=index; --i ){
data[i+1] = data[i];
}
count ++;
data[index] = value;
}
只要修改一下循环的方向,从后往前执行,就可以得到正确的结果。
元素删除
有了插入的前车之鉴,我们很容易能想到元素删除要如何处理。 只需要将待删除元素后面的元素都向前移动一位即可:
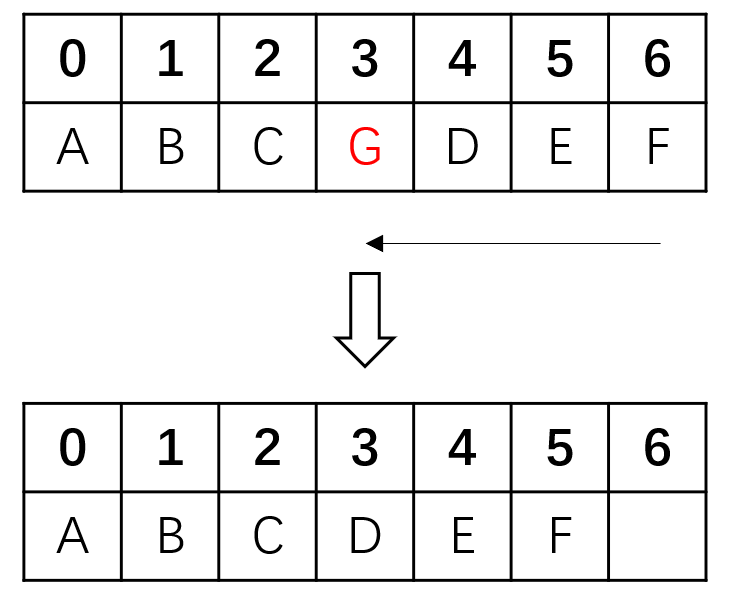
与插入不同的是,这次我们向前移动,为了防止相互覆盖。元素移动的次序必须从前向后执行:
void SEQUENCE::remove(int index){
for( int i=index+1; i<count; ++i ){
data[i-1] = data[i];
}
count--;
}
这里就请大家自行测试了。
思考一下
append,insert和remove这三个函数(最坏)的时间复杂度分别是多少?
这就结束了吗?
实际上并没有,因为你的测试不够充分! 只用简单的数据进行测试很有可能让你的提交得到一个partial。
我们当然很难测试完所有的情况,但将边界好好测试一遍却是能做到的。
插入和删除这两个操作,我们都应该多考虑一下,当我们在头部和尾部插入时,是不是可能存在问题。
为什么需要测试头部,也就是index=0的位置?因为你可以看到我们的代码里使用了-1的操作,0-1可能导致溢出或者数组越界问题。同理尾部元素也可能导致数组越界问题。
因此我们应该合理的构造测试用例,对以下四种情况进行测试:
- 元素插入头部
- 元素插入尾部
- 元素插入尾部(即下表是
count的位置,等于append) - 删除尾部的最后一个元素
具体如何构造用例并测试,就留给大家自行解决了。
取元素
由于顺序表顺序存储的特点,他可以被视为一种可变长度的数组,同时也具有数组随机访问快速的优势。即我们可以很容易通过data[i]来获得第i号元素。 这在一些需要随机访问的场合非常有用。
int& SEQUENCE::get(int index){
return data[index];
}
显然这一操作的复杂度是。
但如果我们需要在里面寻找某个值,则无法做到以的复杂度得到。
对于无序的数据,穷举是唯一的办法:
int SEQUENCE::search(int value){
for( int i=0; i<count; ++i ){
if(data[i] == value)
return i;
}
return -1;
}
显然这个函数的复杂度是
思考题
下面是几道思考题留给大家:
- 在何种情况下,我们可以进一步降低值搜索的复杂度,如何做到?
- 当我要删除一个区间时——例如从3到8号元素——应该如何操作?
- 同理,当我要在3这个位置插入5个连续的元素,我应该如何操作?
- 我们上面的讨论均不考虑预留的空间被完全填满的情况(即size==count),假如出现了这种情况,你认为应该如何处理?
- 你认为在什么情况下使用顺序表是合适的,而什么情况下是不合适的。
作为大家掌握的第一个数据结构,本节会保证代码都可以运行,但后续的代码则不一定。演示的数据我们统一用
int。 ↩︎属性和方法是面向对象的术语,属性就是成员变量,方法就是成员函数。以后就不再特别说明这两个属于了。 ↩︎
注意这里的设计过程,我们先考虑了需要哪些操作,然后才考虑需要用哪些属性来实现它。 ↩︎
行业里把指向已经销毁空间的指针称为野指针。野大概指的是这个指针不受控制。野指针,飞指针(错误地赋值指针导致指针指向未知空间)在工程上是非常令人头疼的问题,因为错误的现象是随机的(偶现),导致问题很难查。与你想的不同的是,这里把不用的指针赋空,并不能保证这个指针不会被误用。但一旦误用了该指针,就会触发错误(0地址通常不能访问),使现象从随机出现变为必然出现,这样问题就好查很多了。 ↩︎