二叉树的遍历

XMUT.SE.DS2022年10月15日大约 16 分钟

二叉树的遍历

对树进行的操作中，我们经常需要针对每个节点做一些操作。例如打印出对应的值，进行数据统计，或者销毁等。这就要求我们需要按一定的顺序访问每个节点。

遍历的类型

线性表的遍历非常简单，因为每个节点的前驱和后继是固定的，次序也是唯一的。但对于二叉树而言，其前驱虽然固定，但后继则有两个，分别是左右子树。我们可以这样用递归的方式描述遍历过程：

遍历二叉树 = 遍历左子树+遍历右子树+遍历根节点

这里的遍历，可以视为某种操作，比如打印或者销毁。

根据遍历左右子树和根节点的不同次序，可以把遍历分为三种：

先序（根）遍历（vlr）：这种遍历先处理根节点，再依次遍历左子树和右子树
中序（根）遍历（lvr）：这种遍历先遍历完左子树，再处理根节点，最后遍历右子树
后序（根）遍历（lrv）：这种遍历先遍历完左子树和右子树，最后再处理根节点

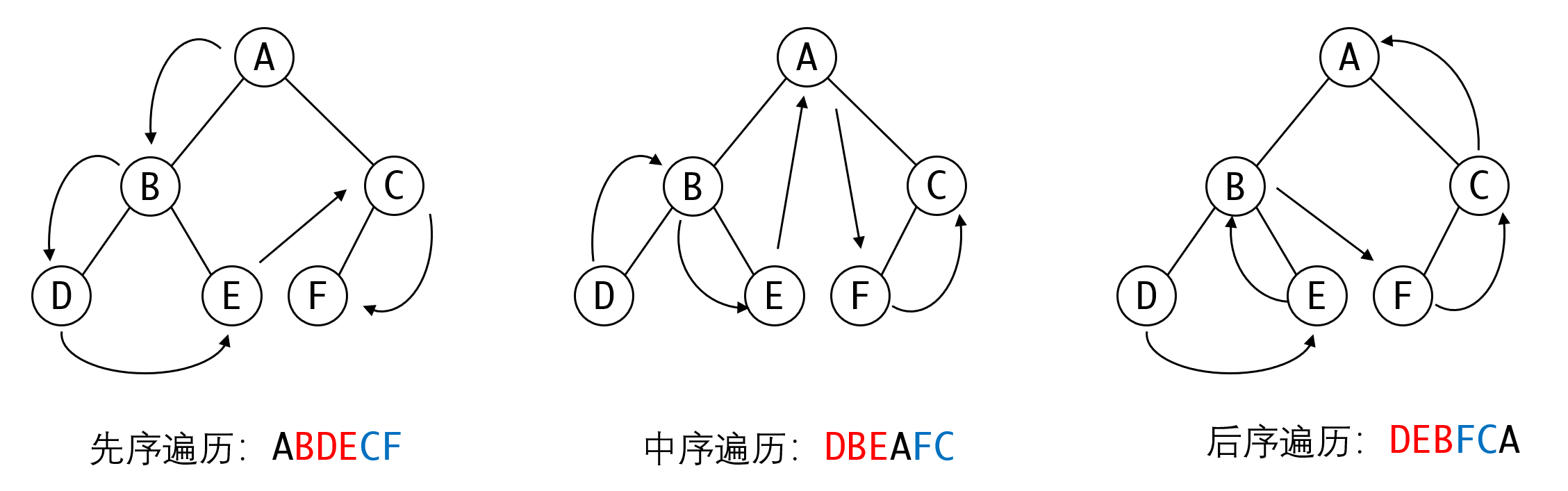
注意这里的遍历是都是递归式定义。

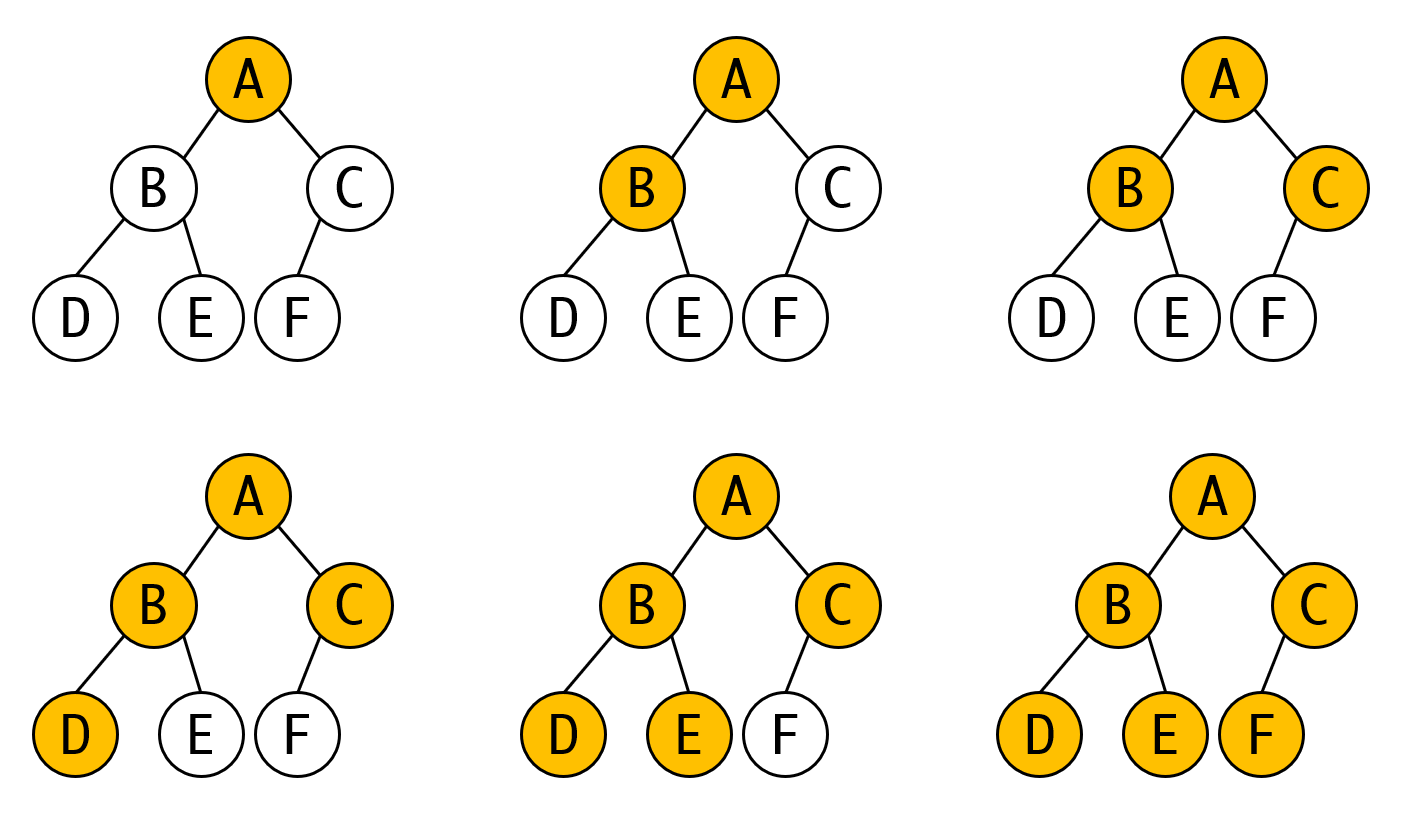
所以当我们说中序遍历，是以左根右的方式进行遍历时，我们的意思是：左子树要遍历完毕，才会处理根节点。从图中我们可以看出，左子树的DBE（红色）都遍历完毕了，我们才访问根A，接下来才访问A的右子树CF（蓝色）。对于左子树BDE这个子树而言，也是先左再根再右。

所以我们可以有很多推论：

如果根节点有左子树，那么中序遍历和后序遍历中，他的最左节点一定是首个被访问的节点。
后序遍历的最后一个节点一定是根节点
三种遍历中，左子树节点一定排在右子树节点之前

......

递归遍历

既然遍历的定义是递归式的，那么用递归来实现是再自然不过的。

我们有如下三种遍历，注意这里我们遍历的操作都用简单的打印值替代，实际中可以有各种操作。

// 先序遍历
void walk_tree_vlr( BTreeNode* root ){
    cout << root->value << " "; // 处理根
    if( root->left_child ){
        walk_tree_vlr( root->left_child ); // 遍历左
    }
    if( root->right_child ){
        walk_tree_vlr( root->right_child ); // 遍历右
    }
}

void walk_tree_lvr( BTreeNode* root ){
    if( root->left_child ){
        walk_tree_lvr( root->left_child ); // 遍历左
    }
    cout << root->value << " "; // 处理根
    if( root->right_child ){
        walk_tree_lvr( root->right_child ); // 遍历右
    }
}

void walk_tree_lrv( BTreeNode* root ){
    if( root->left_child ){
        walk_tree_lrv( root->left_child ); // 遍历左
    }
    if( root->right_child ){
        walk_tree_lrv( root->right_child ); // 遍历右
    }
    cout << root->value << " "; // 处理根
}

每一行代码都与我们之前的的算法描述一致，不必过多解释。

思考

我们常说，递归函数最重要的是两部分，递推方式和停机条件。

在这个例子里，递推方式是非常清晰的，那么请问停机条件是什么？怎么做到的？

树和递归

如果你对递归掌握不是很熟练，那么现在是重新捡起来并认真掌握的时候了。

与之前的很多递归算法（例如阶乘）不同，树的三种遍历蕴含着很多递归的奇妙之处。

为何仅仅通过改变某个语句的位置，就可以实现三种完全不同的操作。
在遍历的过程中，调用栈又发生了什么样的变化？
中序和后序遍历是如何保证最左的节点被首次访问到的。
为什么后续遍历一直到最后才会访问root。

等等这些问题，都可以通过仔细琢磨这个递归过程得到解答。如果你能真正弄清楚整个递归的过程，你对递归和函数调用的掌握必然会更上一层楼。

实际上树的大多数算法，都可以通过递归来实现。

如果你是比较老练的程序员，必然对上述写法会有所不满——逻辑太过复杂了。我们通过两个if避免在没有左右子树时出现内存访问错误，那么有没有更简洁的写法呢？

有的：

void walk_tree_vlr( BTreeNode* root ){
    if( root == nullptr )
        return;
    cout << root->value << " "; // 处理根
    walk_tree_vlr( root->left_child ); // 遍历左
    walk_tree_vlr( root->right_child ); // 遍历右
}

上面这个算法就要简洁的多了，那么这个算法和前面的先序遍历算法有什么区别吗？

思考一下

你可能会很迷惑，为什么我们会需要三种遍历。

答案是他们都有用。

从人类理解的角度来说，先序遍历是非常自然的遍历方式。同时他保证在遍历到某个节点时，他的父节点一定存在。

中序遍历我们后面会讲，他在搜索树上非常有用。

后序遍历，则可以保证在处理根节点的时候，左右子树都已经被处理完了。

那么你能想到什么场合，是需要用先序遍历来解决的，又有什么场合，需要用后序遍历来解决的吗？注意这里可以不用局限在二叉树上。

非递归遍历

递归遍历可以让大家更好地理解遍历的过程，但递归调用深度不可控，还有较大的调用开销，实际工作中，我们很少会使用。因此我们还需要掌握迭代式非递归遍历的方法。

在开始讲解非递归遍历之前，我们先要问一个问题：

在之前栈和队列的章节我们已经说过，存在两种遍历方式。一种是深度优先遍历，用栈实现；另一种是广度优先，用队列实现。那么我们自然会想到：这三种遍历方式，哪种是深度优先，那种是广度优先呢？

回答是，这三种遍历都是深度优先遍历。注意他们遍历的特点，在一旦进入左右子树，就一定要遍历完成，这是深度优先遍历的特点。既然是深度优先遍历，那么就应该用栈来解决。实际上，从递归和栈的关联上看，我们也可以看出这里我们需要用栈解决问题。

先序遍历

先序遍历的过程基本是显而易见的。从栈中每弹出一个元素，就将其对应的左右子节点入栈。重复这一过程即可。

1. 将root根节点入栈
2. 从栈顶弹出一个节点，进行处理
3. 如果左右节点存在，将其入栈
4. 重复这2~3直到栈空

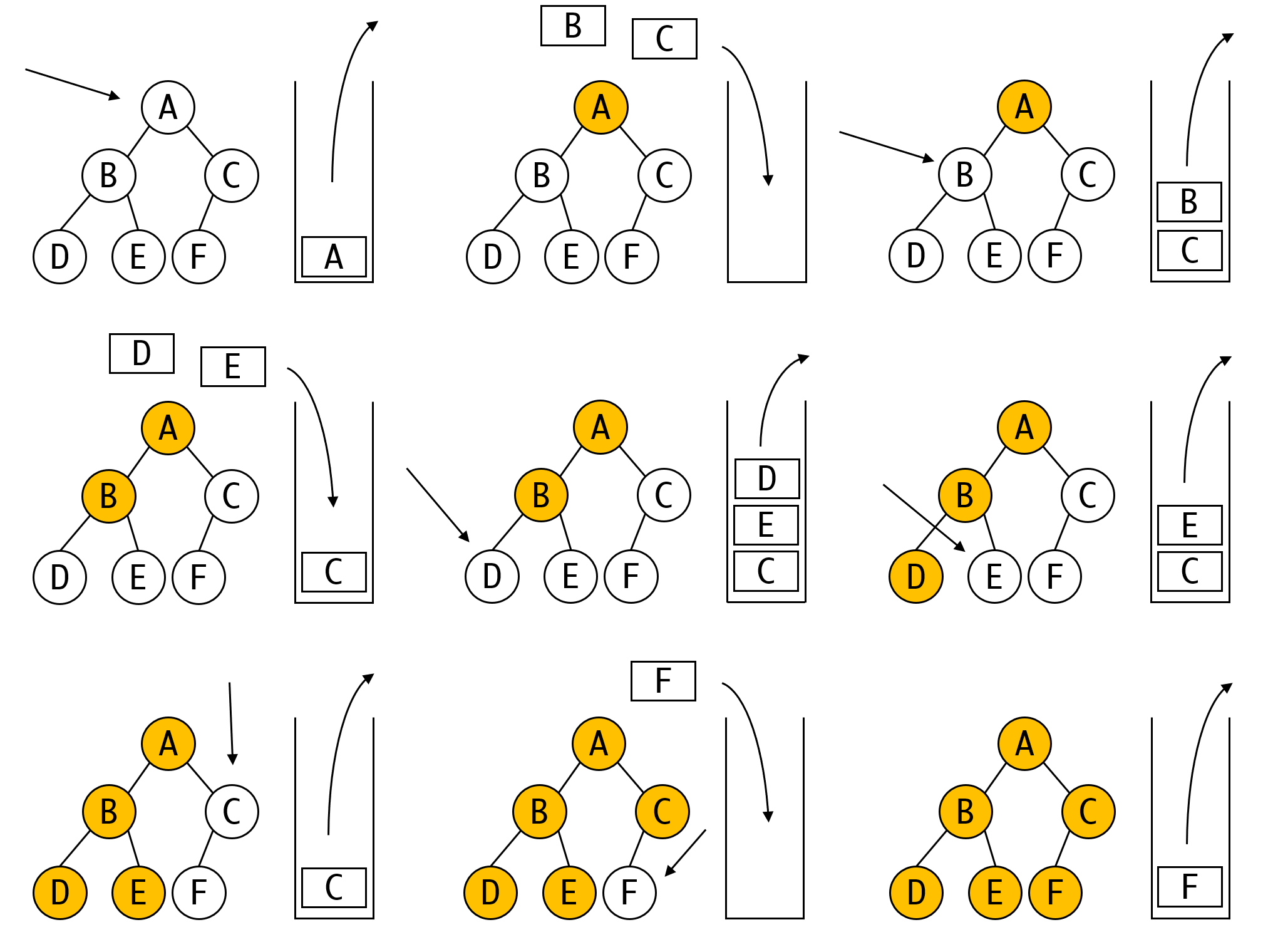
先序执行过程

我们很容易写出他的对应代码：

void walk_vlr_no_recur( BTreeNode* root ){
    stack<BTreeNode*> s;
    s.push(root);
    while(!s.empty()){
        BTreeNode* node = s.top();
        s.pop();
        cout << node->value << " ";
        if(node->right_child)
            s.push(node->right_child);
        if(node->left_child)
            s.push(node->left_child);
    }
    cout << endl;
}

要注意压栈的次序，因为我们出栈必须先左右后，根据栈的性质，入栈次序就必须颠倒过来，先右后左。

非递归中序遍历

从中序遍历开始，迭代的方式就不是那么直观了。这其中要注意的是，栈顶节点何时可以出栈。

先序遍历的次序是，先根，后左右。因此在栈顶遇到某个节点时，就可以将其弹出并处理。因为此时左右节点才入栈，他们必然在根节点后处理。

但中序遍历中则不可以如此处理。当首次遇到某个节点时，此时他的左节点（以及左子树）还未被处理。根据中序遍历的要求，必须优先处理左子树，当左子树处理完毕之后，才能将该节点弹出处理。此时已经是我们第二次遇到该节点了。

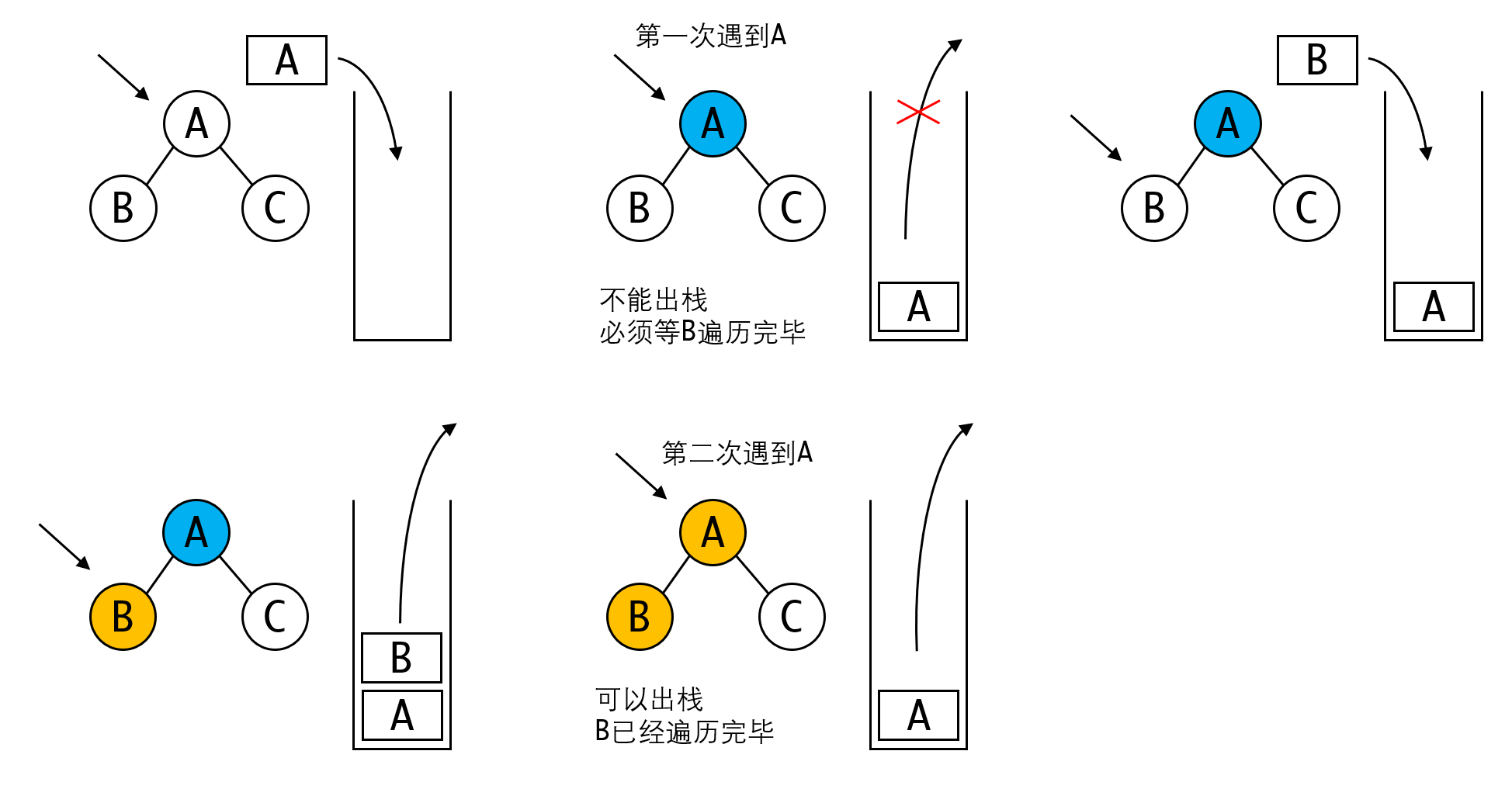
中序遍历的节点次序

对此我们有个比较简单的解决方案——用标记记录某个节点是否被访问过。那么我们可以得到以下的算法：

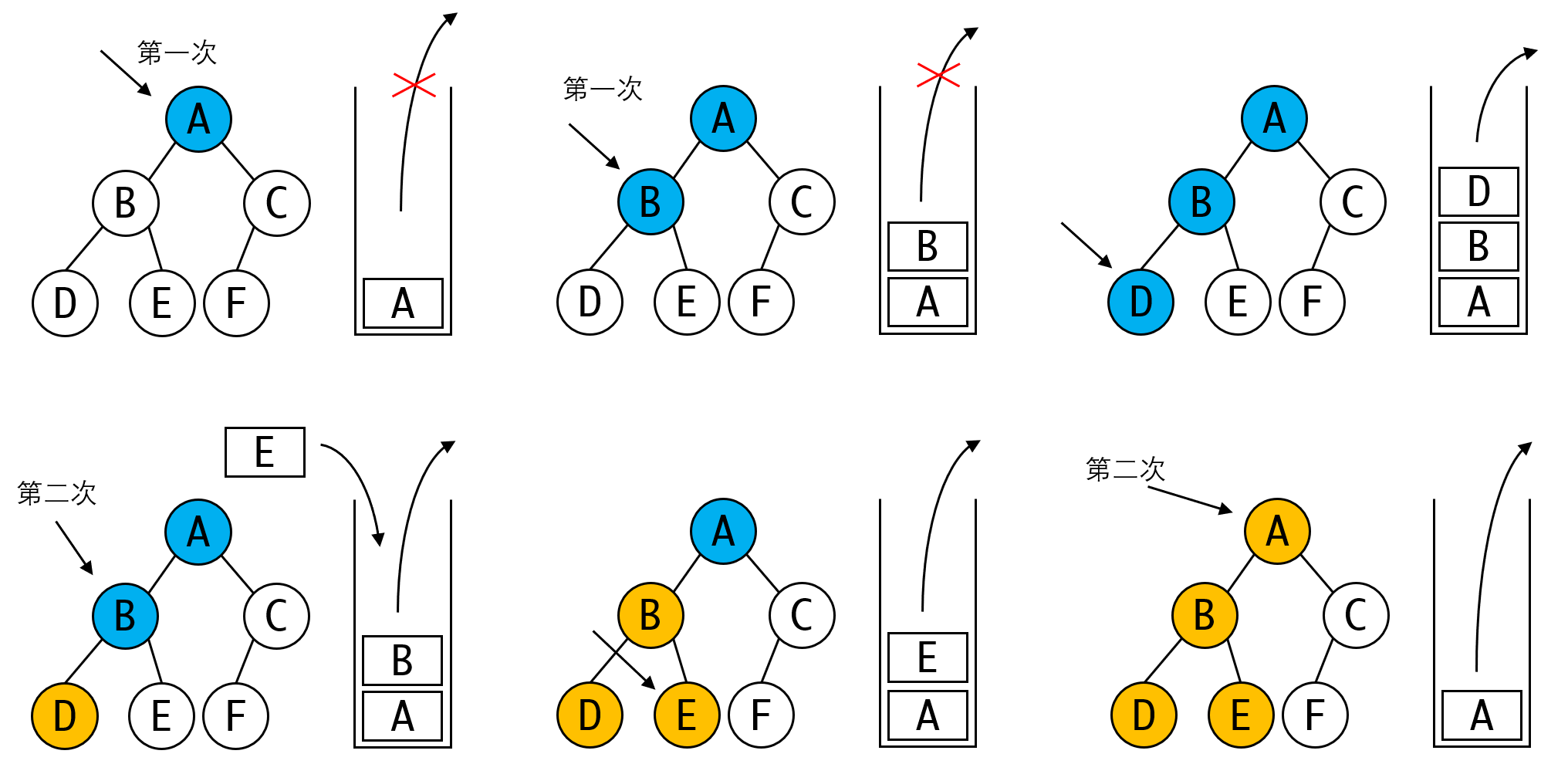
1. 将根节点root入栈
2. 如果栈顶元素的左节点为空，或者左节点已经被访问过，则走3，否则走4
3. 将栈顶元素出栈并处理，然后将右节点入栈。同时在根节点上打上已访问标记
4. 否则将左节点入栈
5. 重复2~4，直到栈空

具体过程见下图：

这一算法过程比较直观。但有一些实现细节需要注意。初学者可能会采用在BTreeNode上增加一个属性的办法来实现：

struct BTreeNode {
    int value;
    BTreeNode* left_child;
    BTreeNode* right_child;
    bool visited; // 是否访问过的标志位
};

但这种方法需要修改对应的结构体定义，很多时候你没有这个权限，或者根本不能这么做。对于这种情况，我们有一种很常用的解决方法，就是所谓的包装类：

struct BTreeNodeWarp{
    BTreeNode* node;
    bool visited;
    BTreeNodeWarp(BTreeNode* node){
        this->node = node;
        visited = false;
    }
};

这样我们将BTreeNodeWarp对象放到栈里，就可以对节点是否被访问进行标记了。请大家自行编写一下对应的代码。

::: tips 包装包装（Warp）是设计模式的一种，他可以扩展功能，而不对原来的代码造成影响。 :::

此外还有另一种比较巧妙的算法

1. 需要一个指针p来记录当前处理节点
2. 令当前处理节点p=root
3. 如果p不空，将p入栈，令p = p->left_child
4. 重复2，直到p为空
5. （此时p等于空），如果栈不空，弹出一个元素top，进行处理，并令p=top->right_child
6. 重复3~5的步骤，直到p空，且栈空

这一算法看起来比较复杂，实则很容易理解，这里open in new window用一句口诀：入栈向左一直走，出栈访问右子树来概括这一过程。

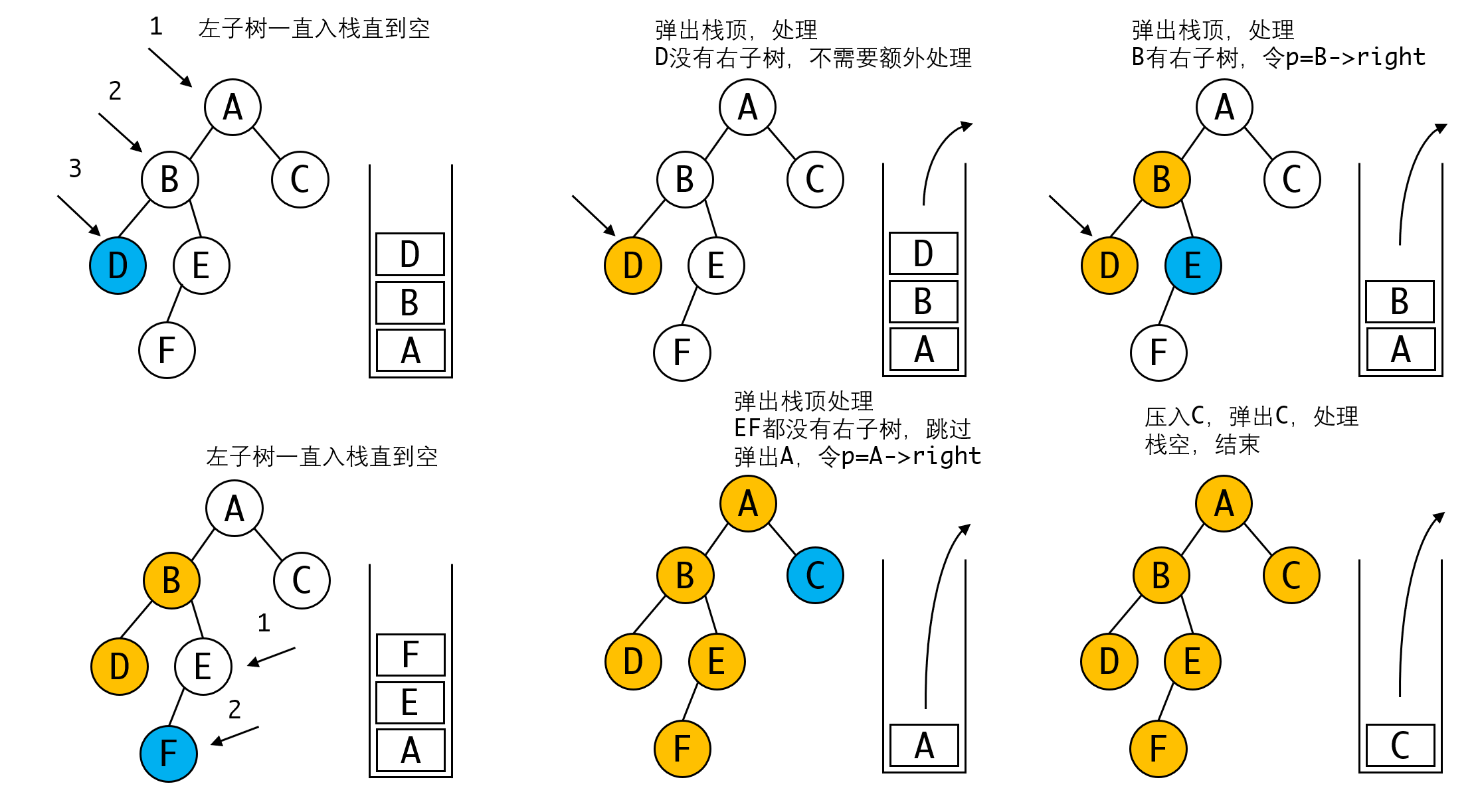
中序遍历过程

实际上这种解法是中序遍历的“标准解法”，他不用额外的标志位，处理起来简洁很多。

请大家自行编写对应的算法。

后序非递归遍历

有了中序遍历的基础，后序遍历也变得很好理解了。中序遍历当首次遇到节点时，要将其左子树入栈。第二次遇到节点时，出栈处理，并将右子树入栈。

而后序遍历则只需要稍加修改，首次遇到节点时，将左右子树入栈（注意次序，先右后左）。第二次遇到节点时就可以直接出栈并处理了。

因此这里也可以通过设置标志位的方式来解决，与中序遍历非常类似，这里不再赘述。

同样后序遍历也有一种比较巧妙的方法来解决。通过观察我们可以发现，节点的访问总在他的左子树或者右子树的被访问之后。针对这点，我们可以设置一个prev，记录前一个被访问的节点，并通过prev与节点左右子节点之间的关系来判断节点是否应该被弹出。

那么什么情况下可以弹出来呢？根据左右子树是否为空，我们可以归纳出四种情况：

左右子树都空，也就是叶子节点，直接弹出。
左右子树都不空，此时prev应该指向右节点。
右子树不空而左子树空，此时prev应该指向右节点。
左子树不空而右子树空，此时prev应该指向左节点。

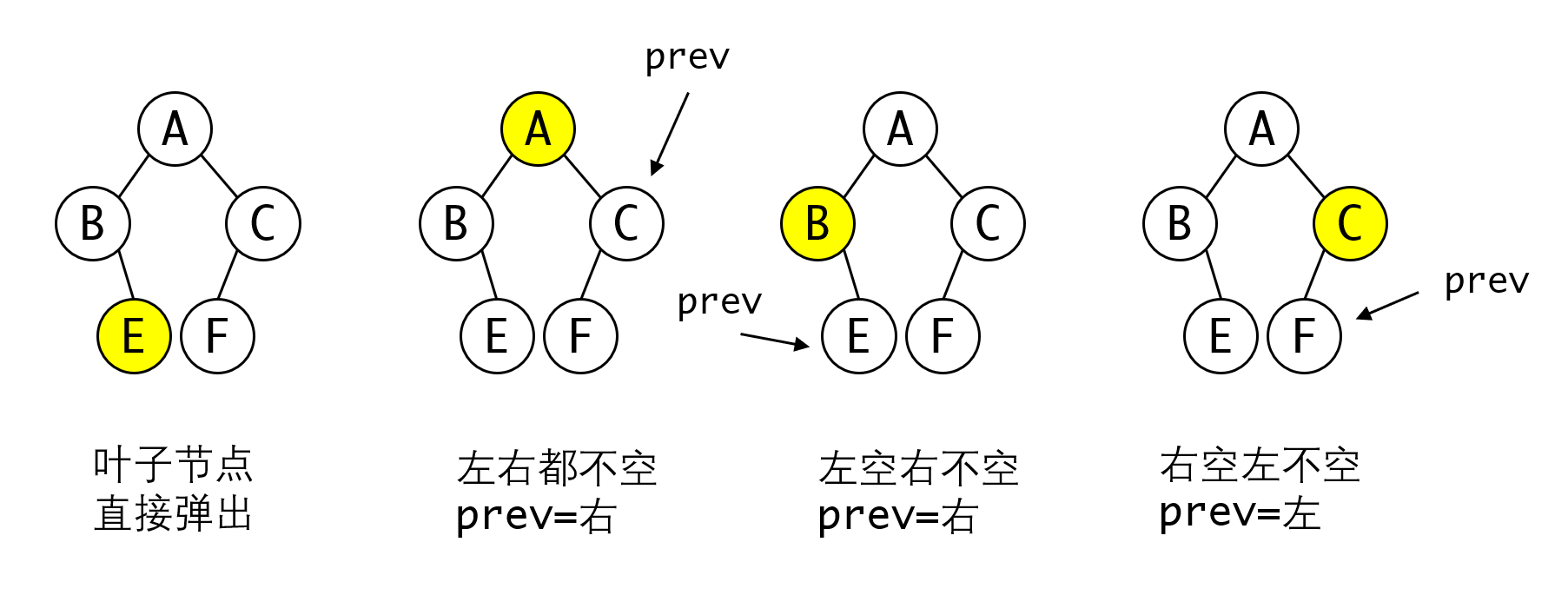
不难发现2、3是可以合并成一种情况的，即右子树不空时，prev应指向右节点。

因此我们可以给具体的算法逻辑：

1. 将root压栈，prev=空
2. 查看栈顶元素top，如果满足以下三点，弹出top并处理，prev=top：
  a. 左右子节点都为空
  b. 右节点不空，且prev等于右节点
  c. 左节点不空，右节点为空，且prev等于左节点
3. 若不满足上述条件，则将右节点和左节点依次入栈
4. 重复2~3直到栈空为止

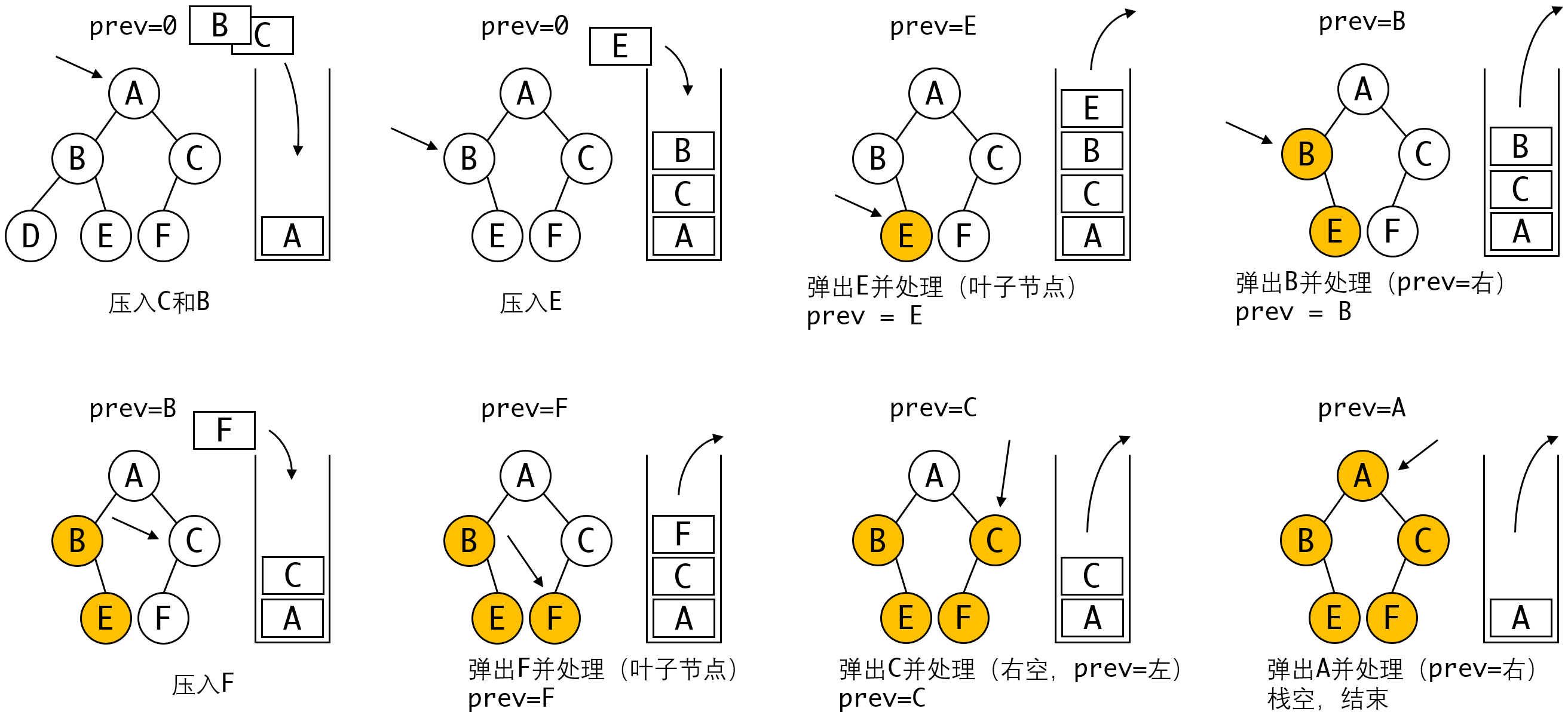
算法代码同样请自行编写。

线索二叉树

遍历的过程实际上将一个非线性的树状结构转变为线性结构。但某些场合下，当我们可能会希望从某个特定的节点开始遍历。此时我们只有一种办法，就是从头开始遍历到该节点，剩下的遍历就是我们需要的：

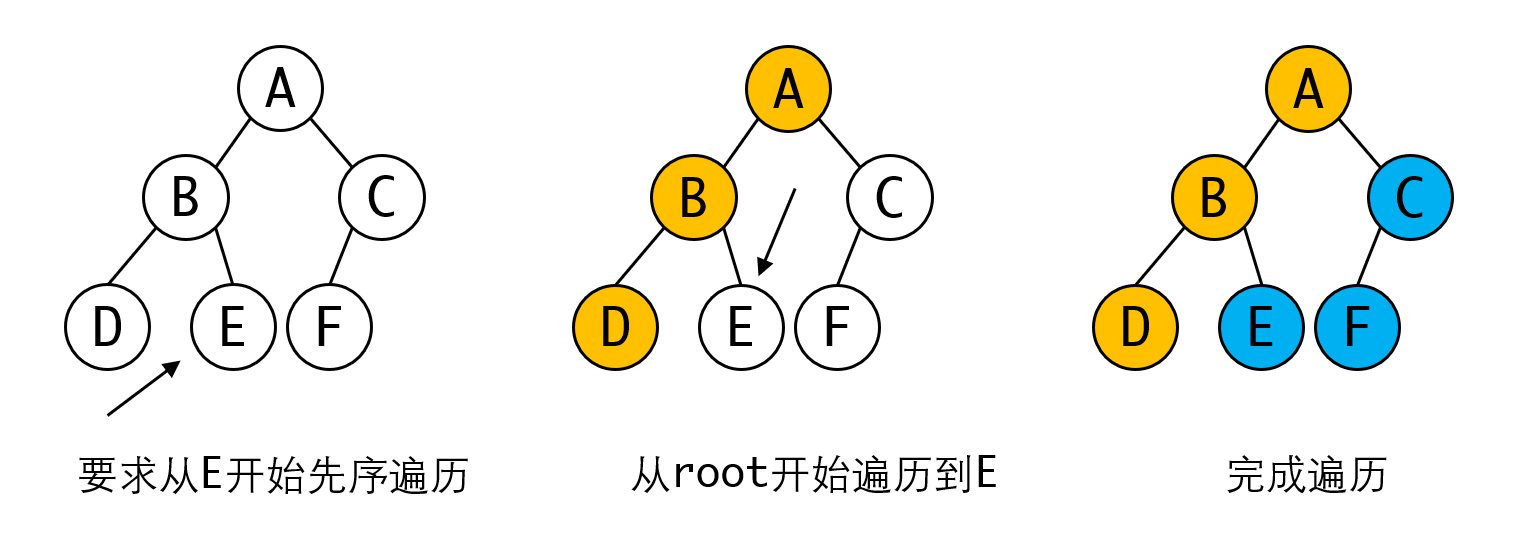
显然这种方法的效率很低，为了提高效率，可以通过一个额外的链表来记录遍历的过程：

struct BTreeNode {
    int value;
    BTreeNode* left_child;
    BTreeNode* right_child;
    BTreeNode* prev;
    BTreeNode* next;
};

这里的prev和next就指向遍历的前向和后向节点。

为什么和书本的不一样

书本的线索树用一个标志位来标识lchild和rchild到底是指向孩子节点，还是指向线索。从授课的角度看，书本上的做法不仅增加了复杂度，也省不了太多空间，最后也有很多问题。

看上图右侧的中序线索树，其中节点A的前驱是E，后继是F，都不是可以通过lchild和rchild直接到达的节点。而A的左右子树都存在，也就无法构建线索。这就使线索的用处大打折扣。

此外这种做法也节省不了太多空间，每个节点都需要两个额外的标志位来表示其指针的用处。如果按习惯用int来存放，那么在32位机上，他的开销和我们这种形式是完全一致的。在64位机上，可以节省一个半个指针的宽度，也就是4个字节。如果用其他类型存放，考虑到对齐问题，在32位机上，两个标志一起占用4个字节，可以节省4个字节。在64位机上可以节省8个字节。这种节省实际上是微乎其微的，同时他导致的逻辑复杂化反而会降低程序运行的效率。

所以现实世界的实现中没有什么人会用书本的方式来实现，尤其在现在空间开销已经基本让位于时间开销的环境里。

但如果你考408，可能你还是要按书本的来。

线索的构建

那么要如何构建线索呢，实际上如果你用非递归遍历的话，因为前后次序非常清晰，构建线索是非常简单的。这里反而是递归遍历更难一些。

那么为什么还要用递归来做呢？

因为可以很好地锻炼你设计递归算法的能力。

我们先考虑先序的情况。

首先我们可以明确一点，即我们需要在遍历的过程中，逐步构建线索。也就是说，线索二叉树的执行逻辑和对应的遍历算法应该是相似的，路径是相同的。

以上图的先序线索树中，我们会发现无论从A->B还是从B->D，即向左遍历时，他的线索都非常清楚，实际上也可以直接获得。我们只需要在向下遍历的时候，将父节点传递给子函数，就可以很容易地构建出这种线索关系：

void walk_tree_vlr( BTreeNode* root, BTreeNode* prev ){
    root->prev = prev; // 构建线索
    if(prev) // 可能为空
        prev->next = root; // 构建线索
    if( root->left_child ){
        walk_tree_vlr( root->left_child, root ); // 向左递归，prev=root
    }
    if( root->right_child ){
        walk_tree_vlr( root->right_child, ???? ); // 右节点的prev是谁？
    }
}

到第8行为止代码逻辑非常清楚，但第10行要向右节点传入prev时，我们应该填什么？

注意观察上图，我们可以发现，右侧的第一个节点C的前驱应该是E，好像平平无奇，但如果你仔细思考一下，你就会发现他是左子树访问的最后一个节点。那么到这里我们就非常清楚了，第10行我们应该填入左子树访问的最后一个节点，因为这个节点是二叉树左子树的最右节点（为什么？），所以我们可以这里求出它，并传递给构建右子树的递归函数：

void walk_tree_vlr( BTreeNode* root, BTreeNode* prev ){
    root->prev = prev; // 构建线索
    BTreeNode* last_node = root; // 思考下，为什么初值设置成root
    if(prev) // 可能为空
        prev->next = root; // 构建线索
    if( root->left_child ){
        walk_tree_vlr( root->left_child, root ); // 向左递归，prev=root
        BTreeNode* last_node = find_right_node(root->left_child);
    }
    if( root->right_child ){
        walk_tree_vlr( root->right_child, last_node );
    }
}

显然find_right_node可以是一个递归函数（虽然没必要）。

但如果仔细考虑一下的话，我们有更优雅的解决方案，让函数返回他访问的最后一个节点，我们就可以直接把函数返回值作为下一步的输入了。

void walk_tree_vlr( BTreeNode* root, BTreeNode* prev ){
    root->prev = prev; // 构建线索
    BTreeNode* last_node = root; // 思考下，为什么初值设置成root
    if(prev) // 可能为空
        prev->next = root; // 构建线索
    if( root->left_child ){
        // last_node等于左子树最后访问的节点 
        last_node = walk_tree_vlr( root->left_child, root );
    }
    if( root->right_child ){
        last_node = walk_tree_vlr( root->right_child, last_node );
    }
    return last_node;
}

同样的，我们其实也有比较简洁的写法：

BTreeNode* build_threads_vlr(BTreeNode* root, BTreeNode* prev) {
    if( root == nullptr )
        return prev;   // 为什么？
    root->prev = prev;
    if (prev) {
        prev->next = root;
    }
    BTreeNode* last_node = root;
    last_node = build_threads_vlr(root->left_child, root);
    last_node = build_threads_vlr(root->right_child, last_node);
    return prev;
}

递归函数是如何设计的？

希望从这个例子里大家能更深入地理解一下递归函数是如何设计的。

首先要确立递归的整体框架，然后再确定参数。这过程中要思考的问题是函数需要什么以及要如何求出函数所需要的东西。

有了先序线索树的框架，请大家自行设计中序和后序的线索树。

层序遍历

还有一种遍历方式，是一层层的遍历，从上到下从左到右。

这种遍历方式，实际上是广度优先搜索的方式。我们都知道广度优先搜索用队列实现。

实现代码就请大家自行编写。

二叉树的遍历

# 二叉树的遍历

# 遍历的类型

# 递归遍历

# 非递归遍历

# 先序遍历

# 非递归中序遍历

# 后序非递归遍历

# 线索二叉树

# 线索的构建

# 层序遍历

二叉树的遍历

遍历的类型

递归遍历

非递归遍历

先序遍历

非递归中序遍历

后序非递归遍历

线索二叉树

线索的构建

层序遍历