最短路径算法

求两个顶点之间的最短路径可以说是图最重要的应用之一。最短路径算法在自动寻路、路径规划等方面有广泛的应用。比如自动路由协议OSPF中就采用Dijkstra算法来进行路由的计算。

按计算的目的不同，我们可以把最短路径算法简单分为单源最短路径和多源最短路径。单源最短路径计算的是从某一个顶点（单源的由来）到所有其他顶点的最短路径。而多源最短路径可以一次算出所有顶点到其他顶点的额最短路径。

单源最短路径Dijkstra

实际上直接用BFS或者DFS都可以求单源最短路径，但他们最大的缺点是缺乏方向性，效率性不如下面要介绍的Dijkstra算法。

算法过程

Dijkstra是最为著名的单源最短路径，他的思想跟Prim算法很类似，都是不断选入顶点，最后扩展到所有的顶点。为此跟Prim算法类似，我们需要记录一个所有顶点与源顶点之间的最短距离数组（向量），随着顶点不断扩展，这个数组的值需要不断刷新。如果需要记录具体路径，还需要记录一个来源顶点的向量。

算法描述为：

集合S表示选入的顶点，集合C表示待选顶点，距离向量为D。
选择C中与源顶点距离最近的顶点V放入S。
更新与C中与V相邻的顶点的距离。
重复2、3直到指定顶点被选入。

我们看一个具体的例子：

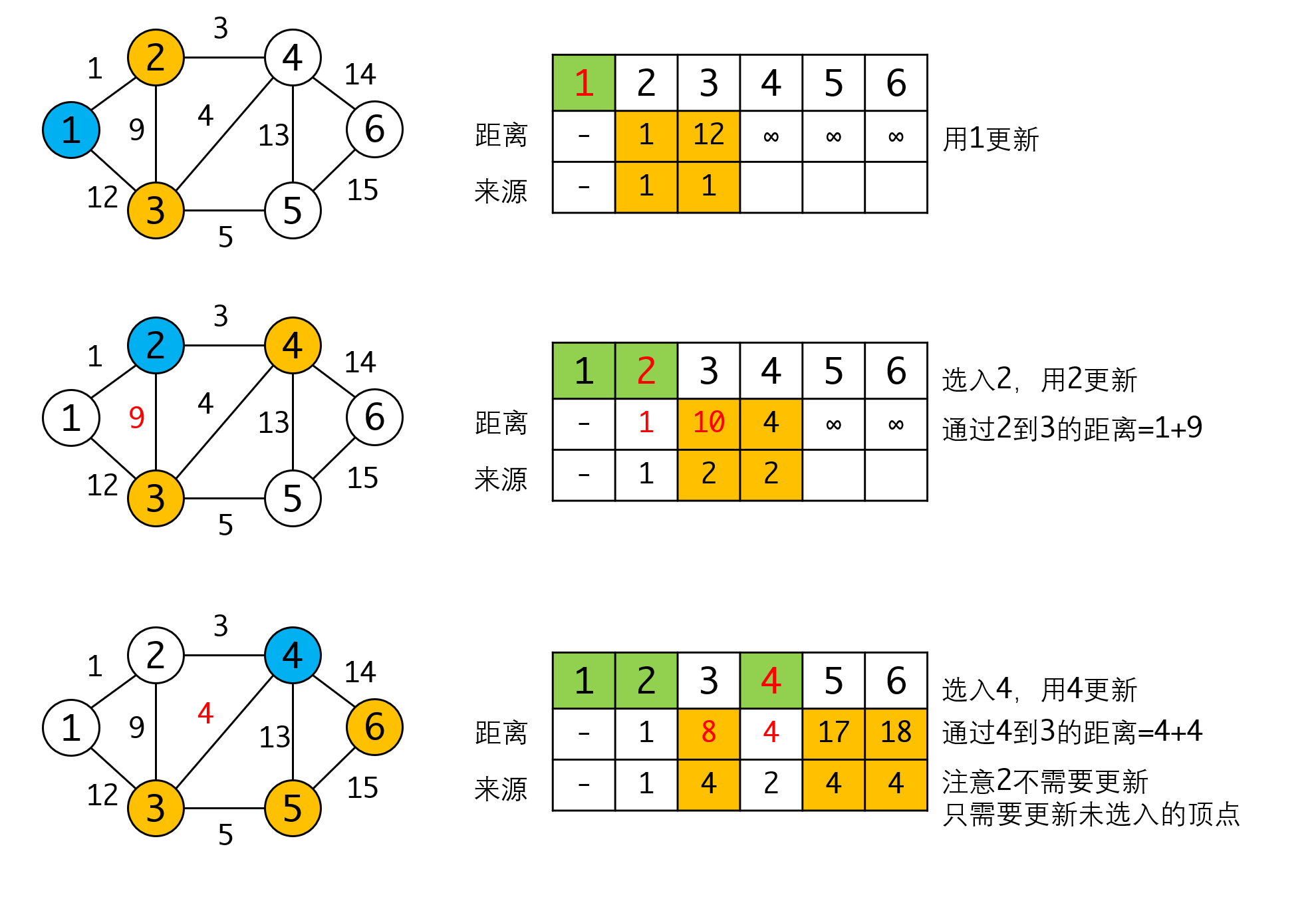
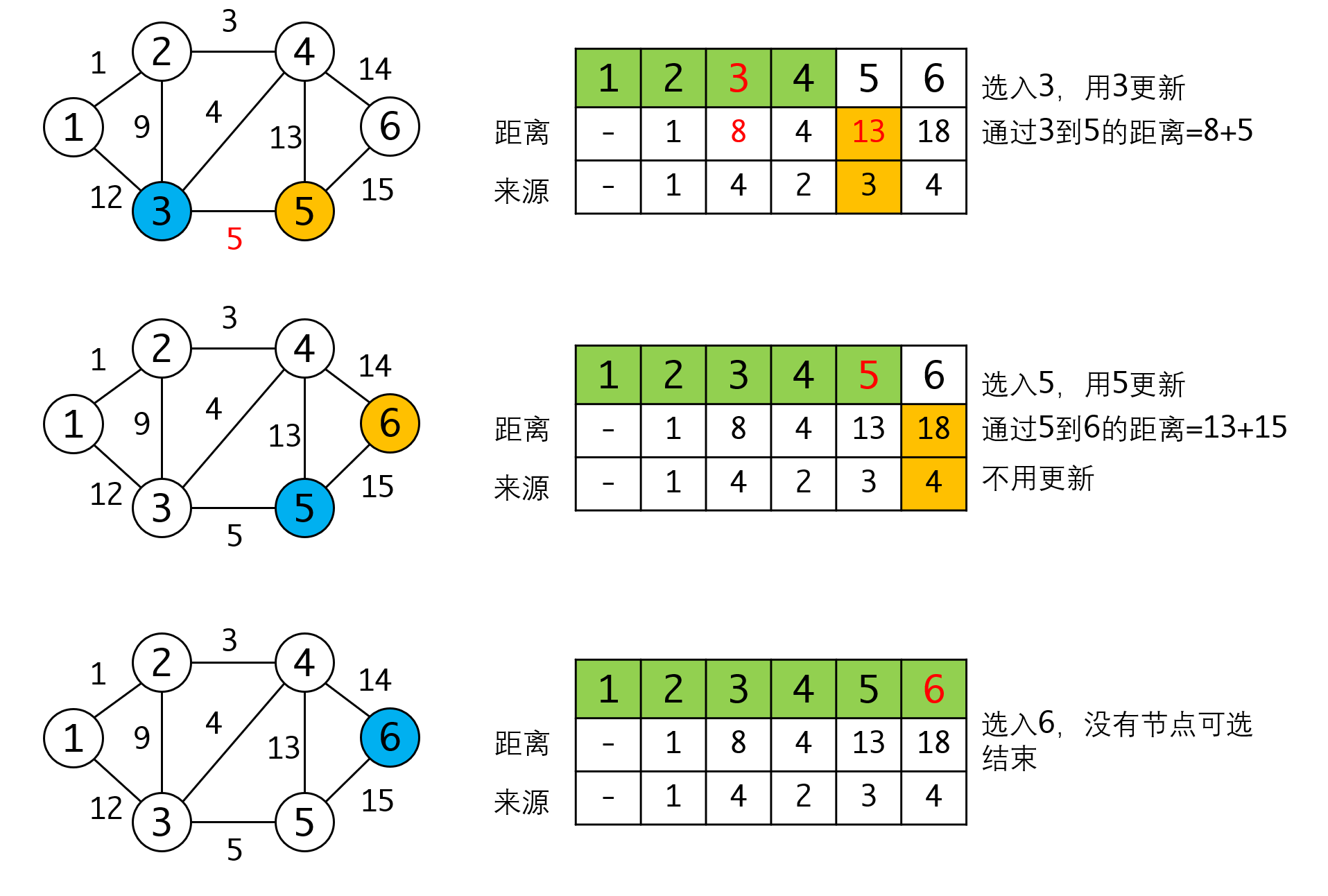
如果要得到具体路径，可以从来源的数组里反推，例如要求到达5和6的最短路径：

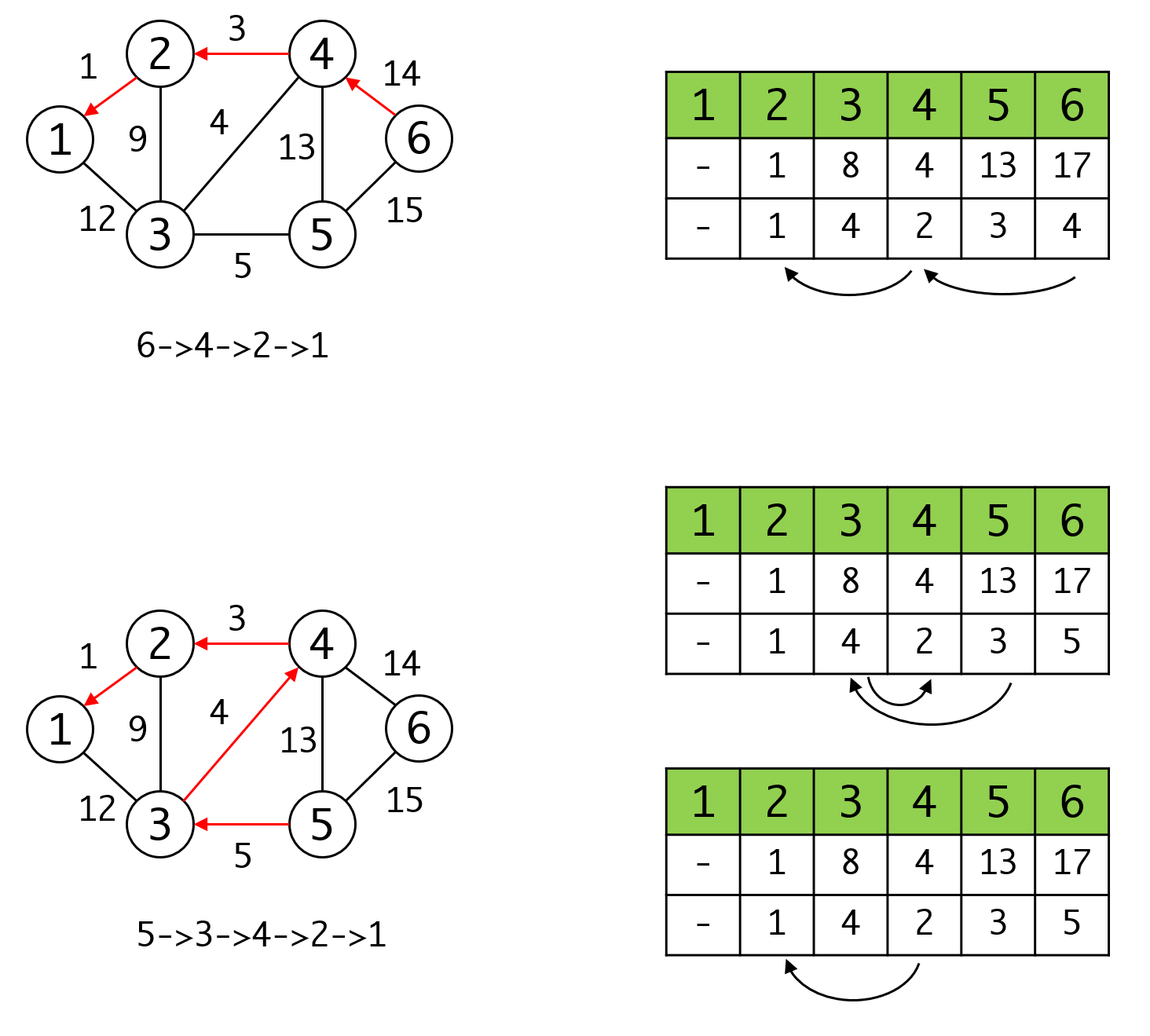
算法特点和优化

Dijkstra算法有这么几个特点：

1. 每回合选入一个顶点，选的是未选入顶点中与源顶点最近的顶点
2. 只用选入的顶点更新，也就是说只需要更新与选入顶点相连的顶点
3. 只更新未选入的顶点，已选入的顶点不需要重复更新
4. 一旦某个顶点被选入，该顶点与源的最短路径就已经确定了，举例来说，上面如果只需要求到4的最短路径，那么第三轮4被选入时，就可以停机了。

Dijkstra算法的更新具有局部性，而且具有比较明显的方向性（都选距离最小的顶点）。相对于DFS和BFS，通常可以更快地到达要求的顶点并停机。而DFS和BFS，如果不将所有顶点都遍历完毕，是无法确定距离就是最短的（为什么？）。

Dijkstra算法每一回合都需要更新一下顶点的距离，这个复杂度是$O(n)$，而整个过程要执行$n$轮，所以复杂度是$O(n^2)$。

而且我们可以用类似Prim算法的优化手段来用堆优化他。跟Prim算法一样，我们每一回合要更新距离。对于这个被更新的距离，直接放入堆中即可。因为堆可以保证拿出的一定是最小的元素，这样我们取出来的一定是符合我们需要的元素。

需要注意的是，Dijkstra算法无法处理负权边。你可以想想为什么。

多源最短路径

用Dijkstra算法也可以算多源最短路径，只需要将算法执行$n$次即可，我们可以得到一个$O(n^3)$的算法。

但Floyd提出的Floyd算法也可以做到，复杂度也是$O(n^3)$，同时在形式上更为简洁。

Floyd算法只需要在邻接矩阵上进行操作即可，如果需要记录路径，我们还需要一个路径矩阵：

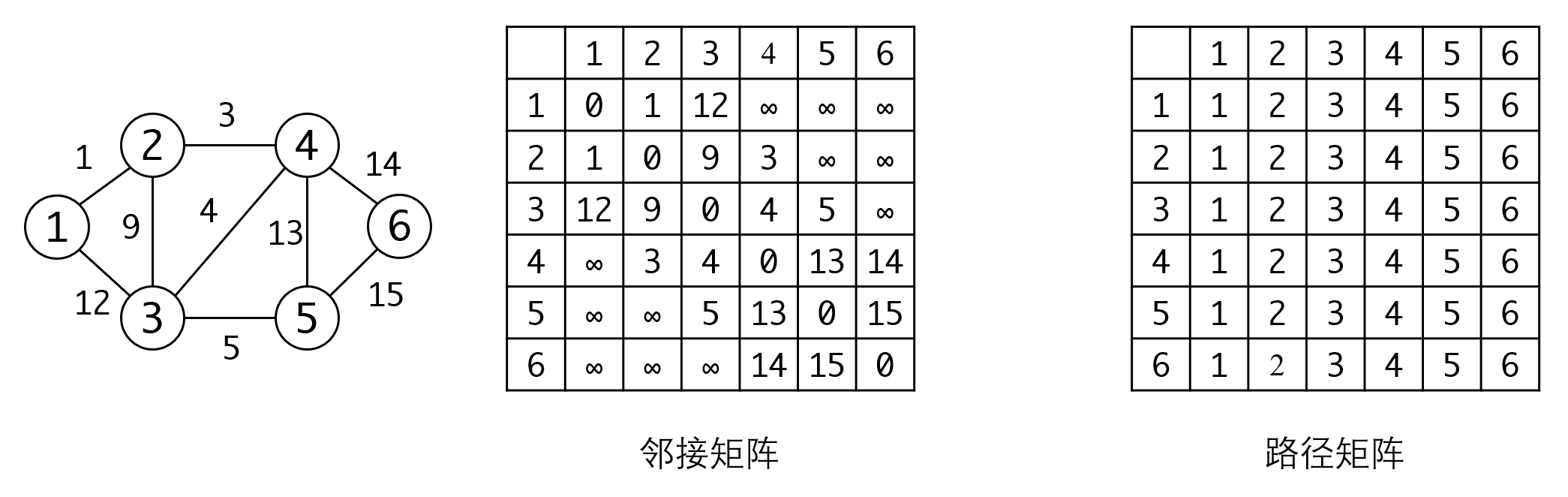
我们要用每一个顶点更新邻接矩阵，将邻接矩阵转变为最短路径矩阵，具体操作是这样的，我们以顶点2更新为例：

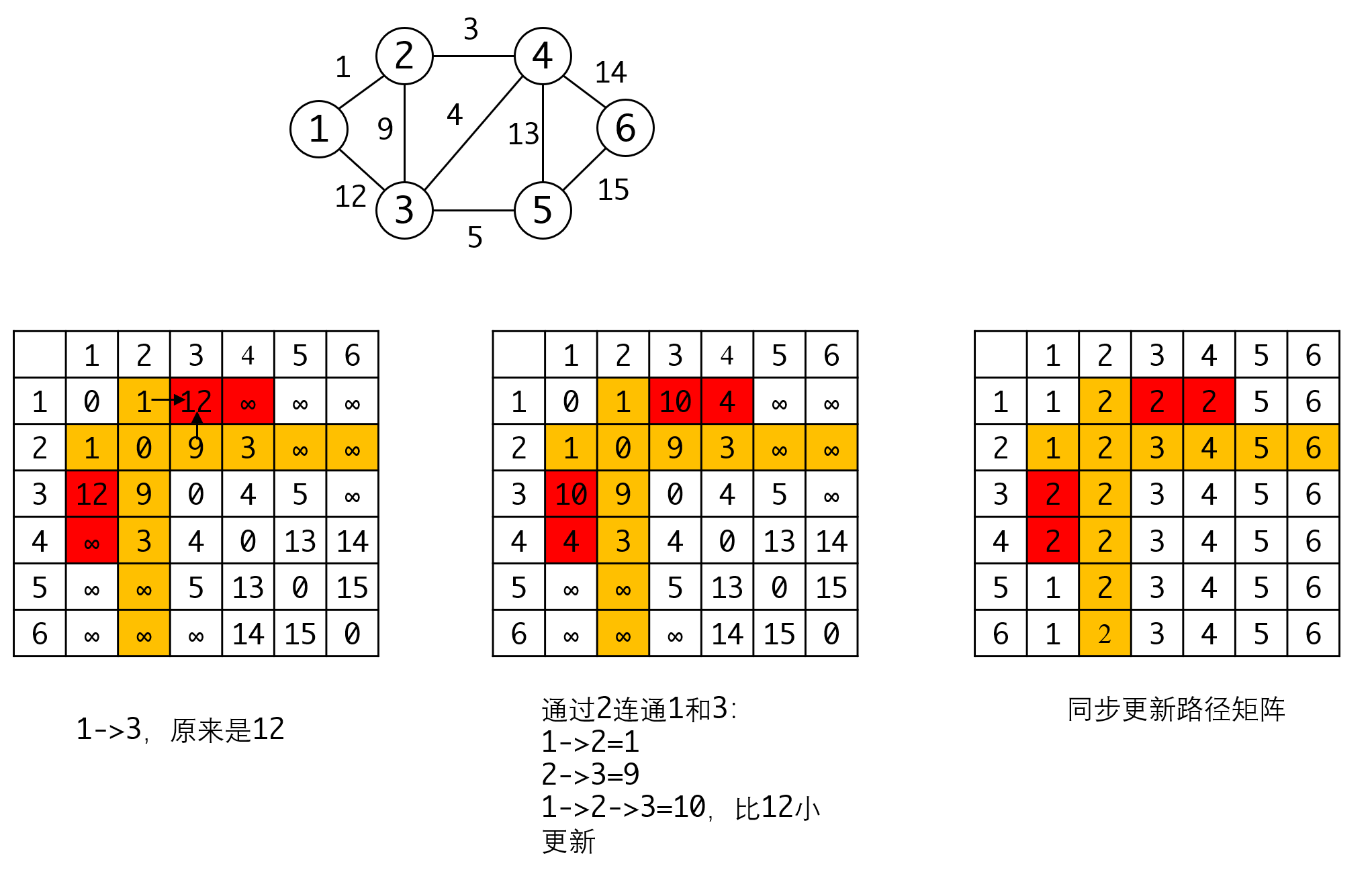
图中原来的邻接矩阵里，1->3有边相连，边长是12。如果通过2中转，1->2的边长是2，2->3的边长是9。所以横竖的的交叉点就是意味着从对应节点进行中转。只要横竖加起来的值小于交叉点的值，就可以用它来更新对应的交叉点：

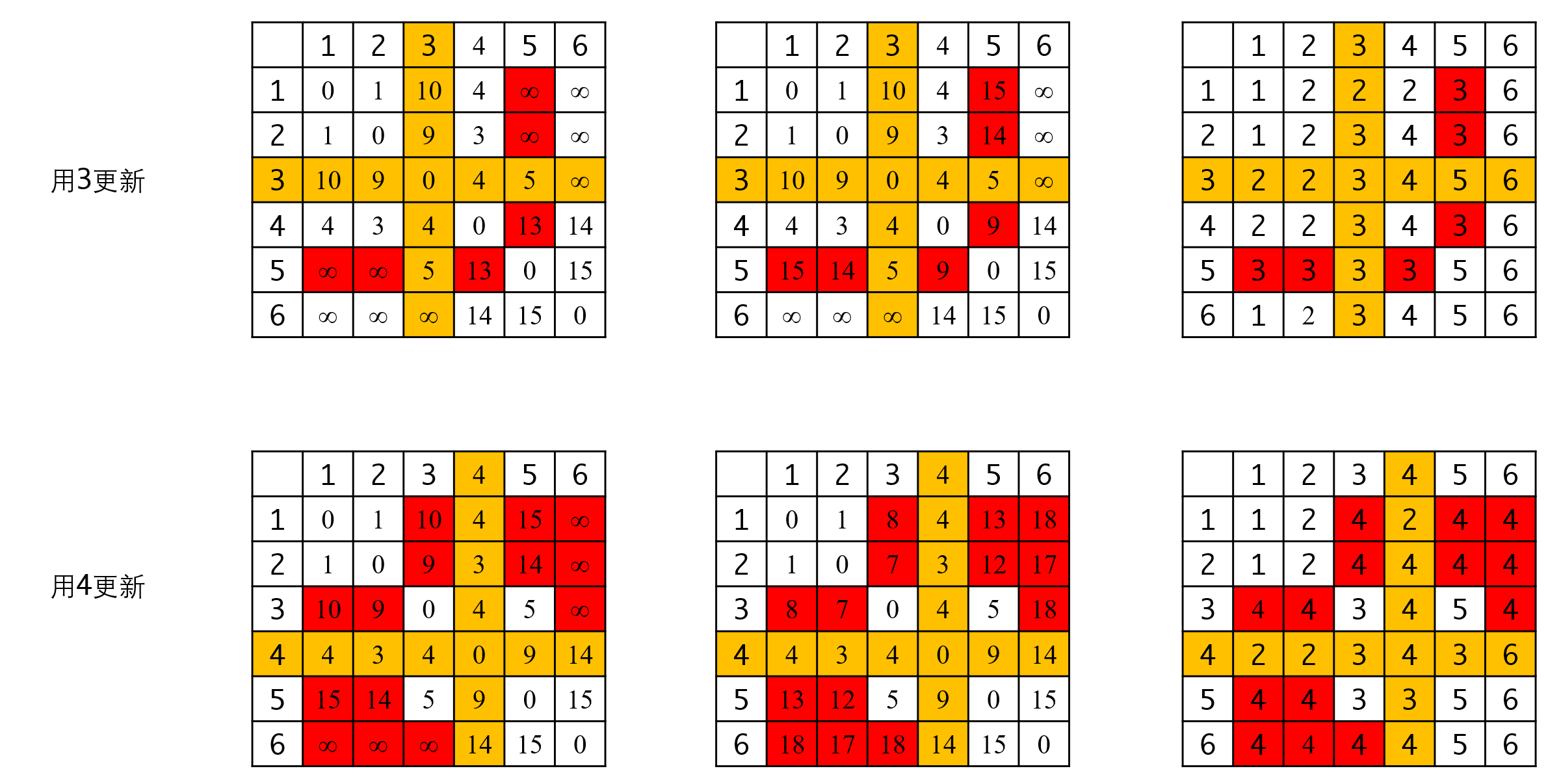
所有顶点都更新完毕之后，邻接矩阵对应位置的值就是两个顶点间的最短路径距离。

Floyd算法的路径推导比Dijkstra算法更复杂一点，是个递归过程：

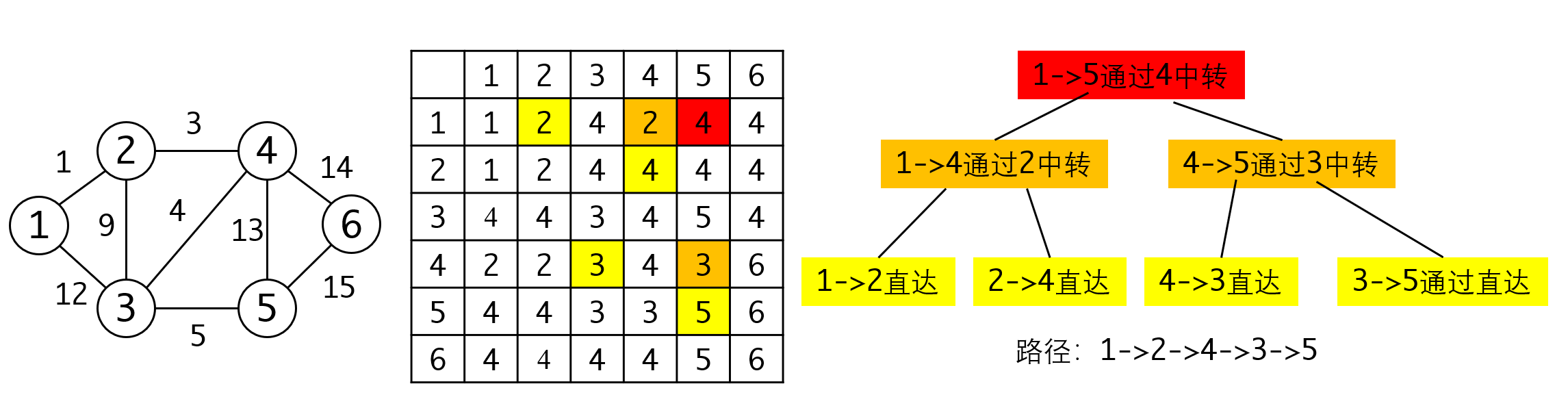
这里给出Floyd算法的伪代码：

void floyd( int n, int adj[][] ){
    for( int k=0; k<n; ++k ){
        for( int i=0; i<n; ++i ){
            for( int j=0; j<n; ++j ){
                if(adj[i][j] > adj[i][k]+adj[k][j]){
                    adj[i][j] = adj[i][k]+adj[k][j];
                }
            }
        }
    }
}

可以看出逻辑确实非常简洁。

Floyd算法的复杂度和Dijkstra算法求多源最短路径一样都是$O(n^3)$，而且要跑满所有循环，因此如果是稀疏图，Floyd算法的效率就比较低，但他胜在逻辑简单。而且Floyd算法只能处理邻接矩阵，无法处理邻接表，因此他的适用范围比Dijkstra算法要小。