定义、术语和存储

定义和术语

与树一样，我们要先介绍一下图的相关定义和术语

显然对于任意的图来说，顶点（Vertex） 和 边（Edge） 都是最基础的组成要素。如果边有方向（即A->B不能推出B->A），我们称为有向图（Digraph）。反之如果边没有方向，则称为无向图（Undigraph）。实际上我们可以把无向图看成一种特殊的有向图，即每条无向边都是两条有向边的组合。

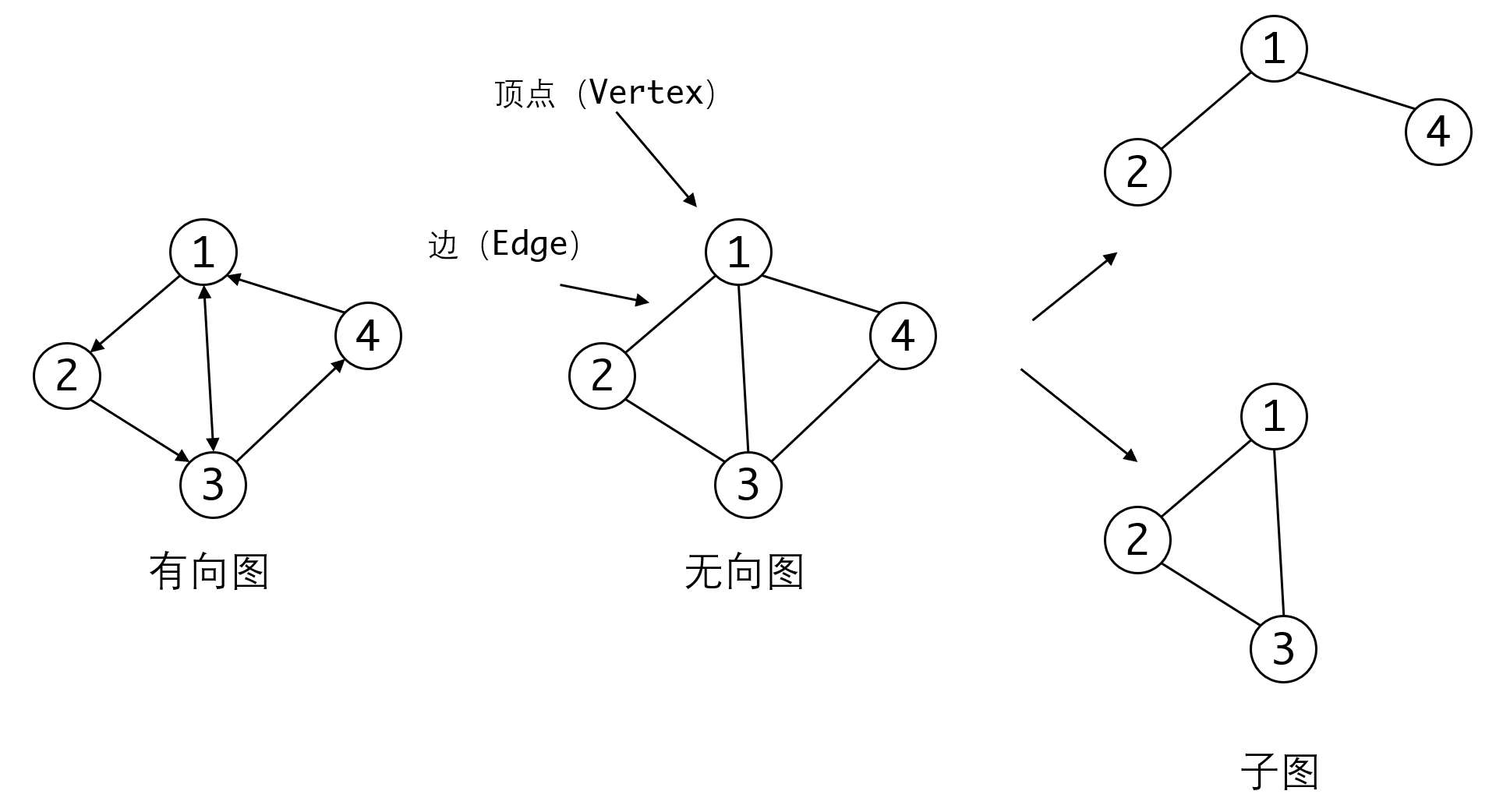
如果我们取出图的其中一部分顶点和边，那么构成的新图称为旧图的子图（Subgraph）。

在此基础上，和树一样，我们会考虑，给N个顶点，最多可以有几条边？这个问题对有向图和无向图的回答是不同的。对于无向图来说，由于同一对顶点之间只能有一条边，所以这个数字是：$C^2_n=n(n-1)/2$。对于有向图来说，一对顶点之间可以有两条方向不同的边，所以这个值是$P_n^2=n(n-1)$。我们称这种边达到最多的图为完全图（Complete Graph），他可以分为有向完全图和无向完全图两种。

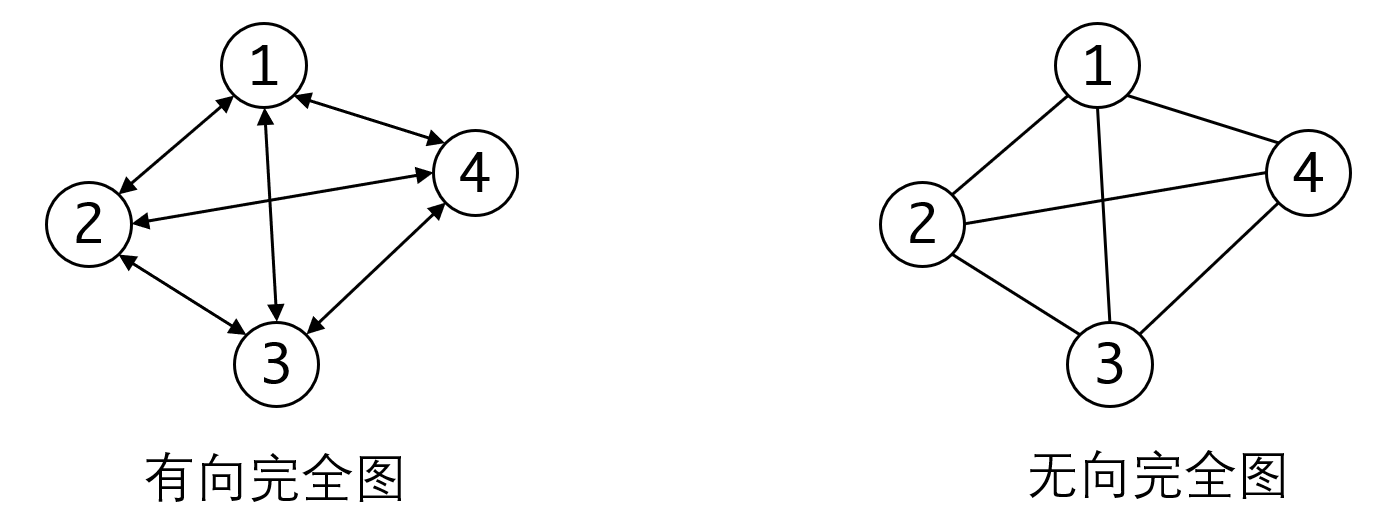
如果一个图的顶点多，而边少，我们称这种图为稀疏图（Sparse Graph），反之如果边多而顶点少，称为稠密图（Dense Graph） 。稀疏和稠密是一个比较模糊的概念，并没有一定的边界。

有些时候我们会赋予图的边一些属性，最典型的比如路径的长，用来衡量两个顶点之间的距离。我们把这种属性称为边的权（Weight）。把这种图称为带权图（Weighted Graph），或者网络（Network）。

如果顶点A有一条边可以到达顶点B，我们说B是A的邻接顶点（Adjacent）。从某个顶点出发的边的数目称为出度（Outdegree），反之进入某个顶点的边的数目称为入度（Indegree）。显然无向图的出度等于入度，可以简单用 度（Degree） 来称呼。

如果从某个顶点出发，能够回到自身，我们称这条能够回到自身的路径为环（Cycle）。有无环路一般在有向图上比较有意义，我们会称这种无环的有向图为有向无环图（Directed Acycli Graph）。而如果一个顶点存在指向自己的路径，我们称这种情况为自环（Self Loop）。注意环和自环的区别：

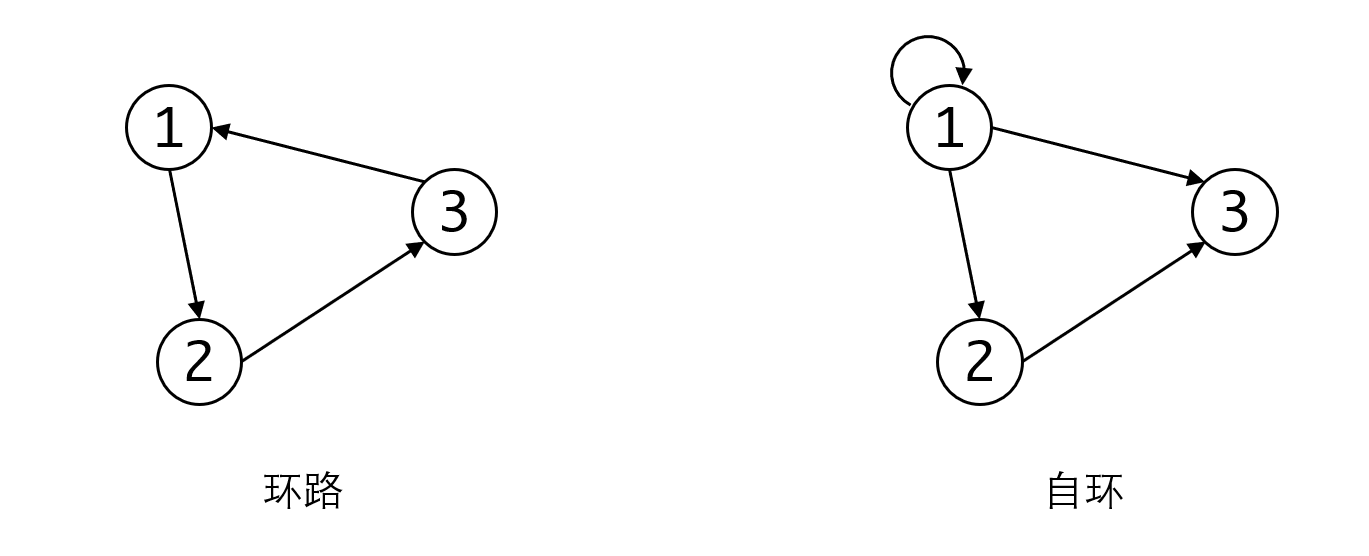
如果一个无向图的任意两个顶点之间都可达，我们把这种图称为连通图（Connected Graph）。同时我们称非连通图的极大连通子图为连通分量（Connected Component）。连通分量这个概念可能不是很清晰，你可以这么理解，他要满足两个条件：

1. 子图本身是连通图。
2. 子图和子图以外的其他顶点都不连通。

对于有向图来说，如果两个顶点可以相互到达。我们称这个有向图为强连通图（Strongly Connected Graph）。强连通图要求要双向可达，因为有向图中$v_1$可以到达$v_2$，并不能推出$v_2$可以到达$v_1$，无向图则没有这个烦恼。同理我们也称非强连通图的极大强连通子图为强连通分量。

图的概念是有点多的，相对于树几乎可以说多了一个数量级。不过大多数的概念名称都很直观。大家要注意理解。

图的存储

图的逻辑结构是我们目前学过的数据结构中最复杂的一种，与之相对的他的存储也是最复杂的一种。不过和我们目前学过的所有数据结构一样，图也既可以用物理上顺序的方式来存储，也可以用链式的方式存储，分别对应邻接矩阵和邻接表。邻接表中又根据组织的形式不同，可以分成邻接表，逆邻接表，十字链表和邻接多重表。

邻接矩阵

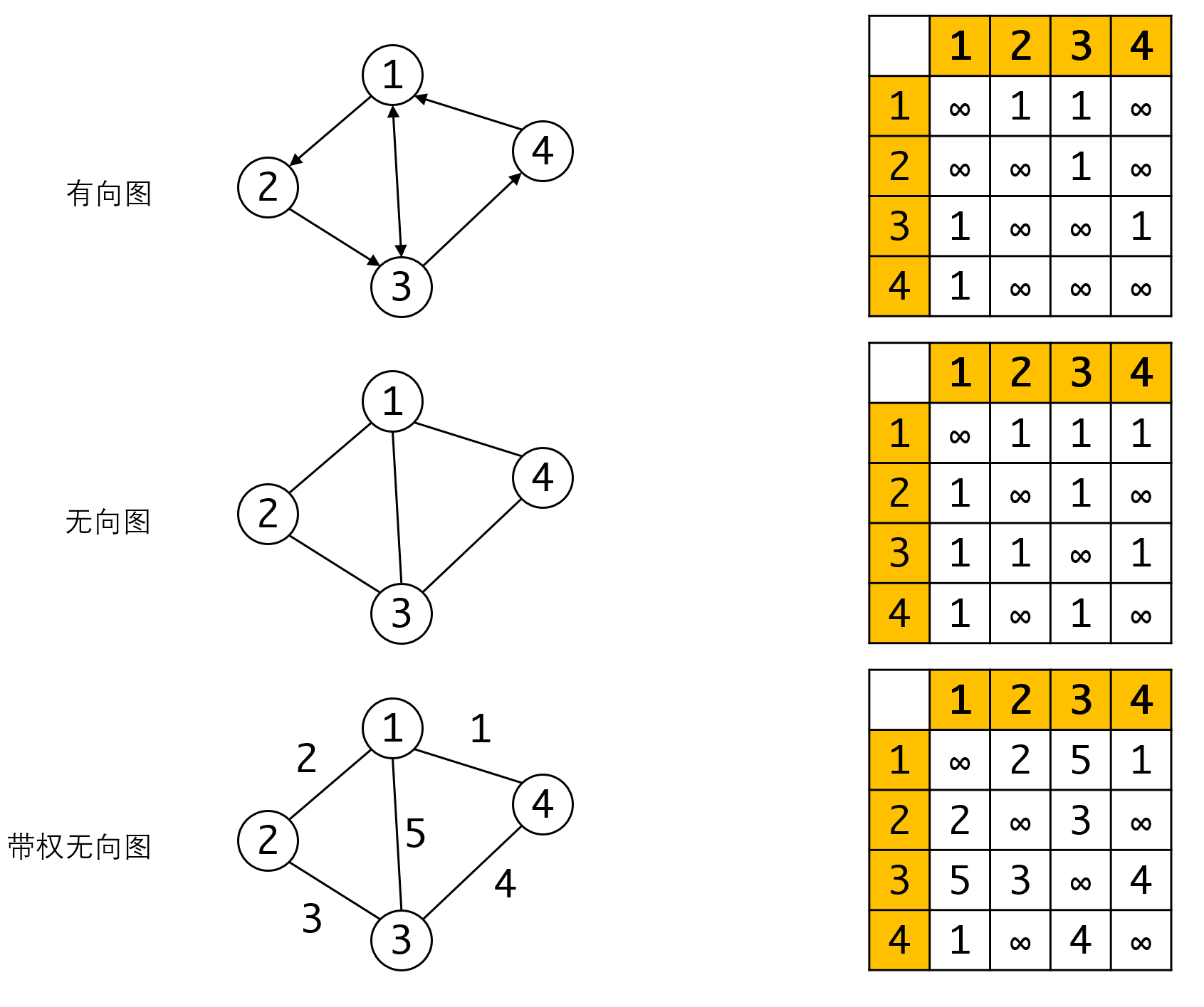
邻接矩阵的表示方式比树的顺序表示方法还要更简单一些。我们用一个二维数组来记录顶点和顶点之间的关系。如果从顶点$i$有到$j$的边相连，那么我们就对数组的第$i$行，第$j$列（a[i][j]）赋值1。而无边相连的顶点，我们就赋值无穷大（可以人为设置一个标志）。

实际上我们是用对应的位置是否为1来记录边。如果需要表示带权图，我们就可以在对应的位置填入边的权值。

思考一下

在邻接矩阵里，要如何求顶点的度，包括入度和出度呢？

注意图中有向图和无向图邻接矩阵的不同，我们可以很容易发现无向图（不管带不带权）的邻接矩阵都是以对角线对称的。 这非常容易理解，无向图中，$v_i$到$v_j$有边，也就意味着$v_j$到$v_i$有变，所以数字总是成对的出现。 而有向图则没有这个性质。

对于无向图的这个性质，我们可以对无向图的邻接矩阵进行压缩，只记录上（下）半个三角形的内容即可，这样可以节省存储的空间。

能节省多少空间？

无向图如果只记录一半的矩阵内容，可以节省多少空间？是一半吗？ 你准备怎么设计？

邻接矩阵的形式非常直观，很容易理解，处理和访问也很容易。但和树的顺序表示法一样，他最大的问题是空间利用率不高，大多数的空间都被无效数据填充了。对于稀疏图，这点就更为致命。

邻接表和逆邻接表

链式存储可以大大提高空间利用率。邻接表的基本原则是，通过顶点上的链表，来表示从顶点出发的边。

我们需要定义两种结构体，分别对应顶点和边：

struct Vertex;

struct Edge{
    Vertex* end;
    int     value;
    Edge*   next;
};


struct Vertex{
    int   value;
    Edge* edges;
}

所有顶点用顺序表（数组）的形式保存，再由这些顶点的edges域来记录边的信息。

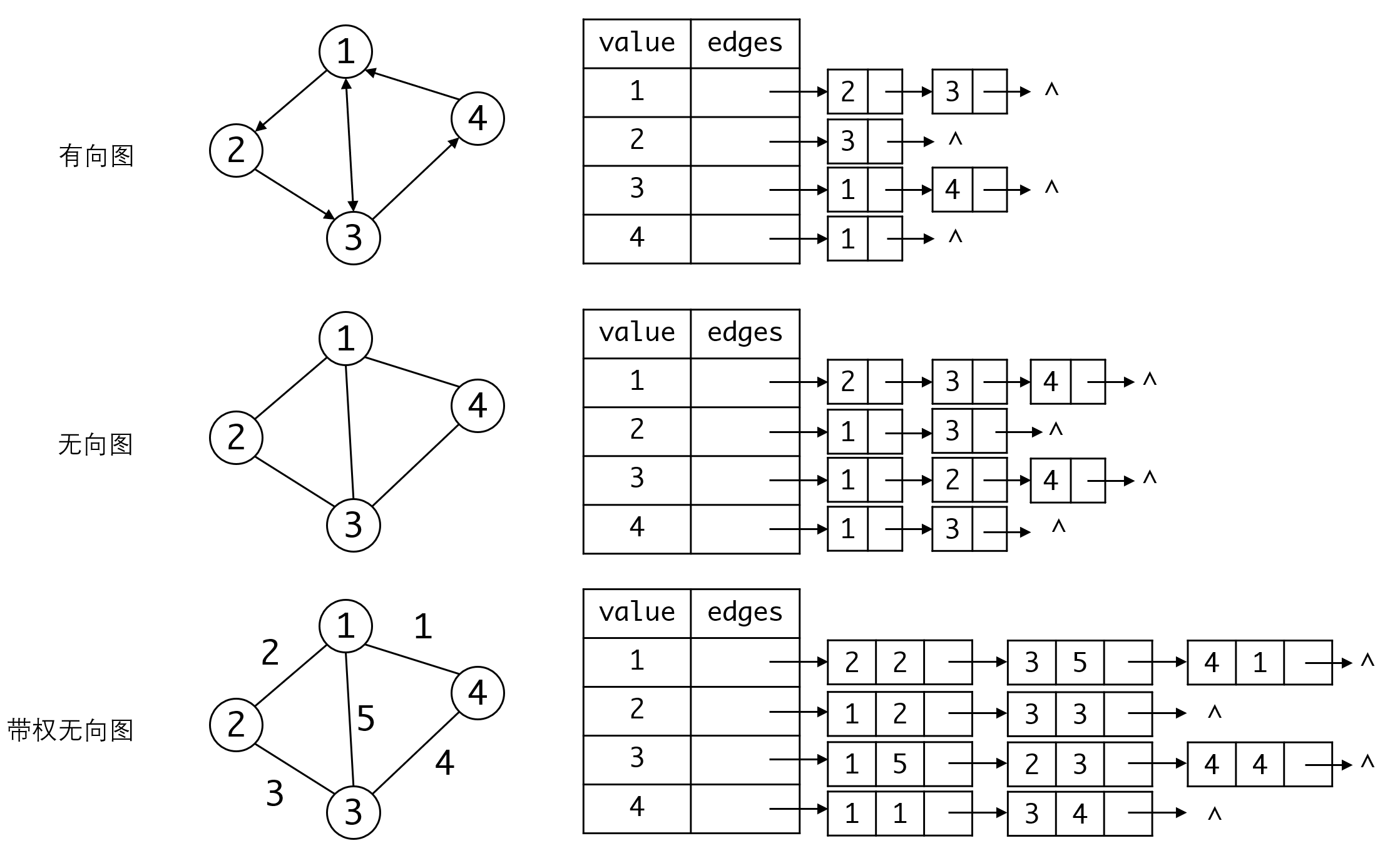
注意边里面虽然填入的是顶点的值，但实际上是顶点对象的数组下标或者指针，这样可以通过边很容易地找到对应的顶点。

当边上需要包含存储一定信息时（例如权重），我们可以用边结构体的value域，否则可以不使用。

从图中我们可以看出，对于无向图，顶点邻接表的数目就是其度。对于有向图，则是顶点的出度。但对于有向图的入度，则没有好的办法。实际上对有向图来说，可以很容易找到顶点的邻接顶点，也就是从该顶点出去的边的终点。但要知道从哪些顶点出发可以到达该顶点则比较麻烦。

思考一下

这两个操作的复杂度分别是多少？

1. 有向图顶点的出度
2. 有向图顶点的出度

为此我们需要引入逆邻接表，顾名思义逆邻接表记录的是以顶点为终点的边：

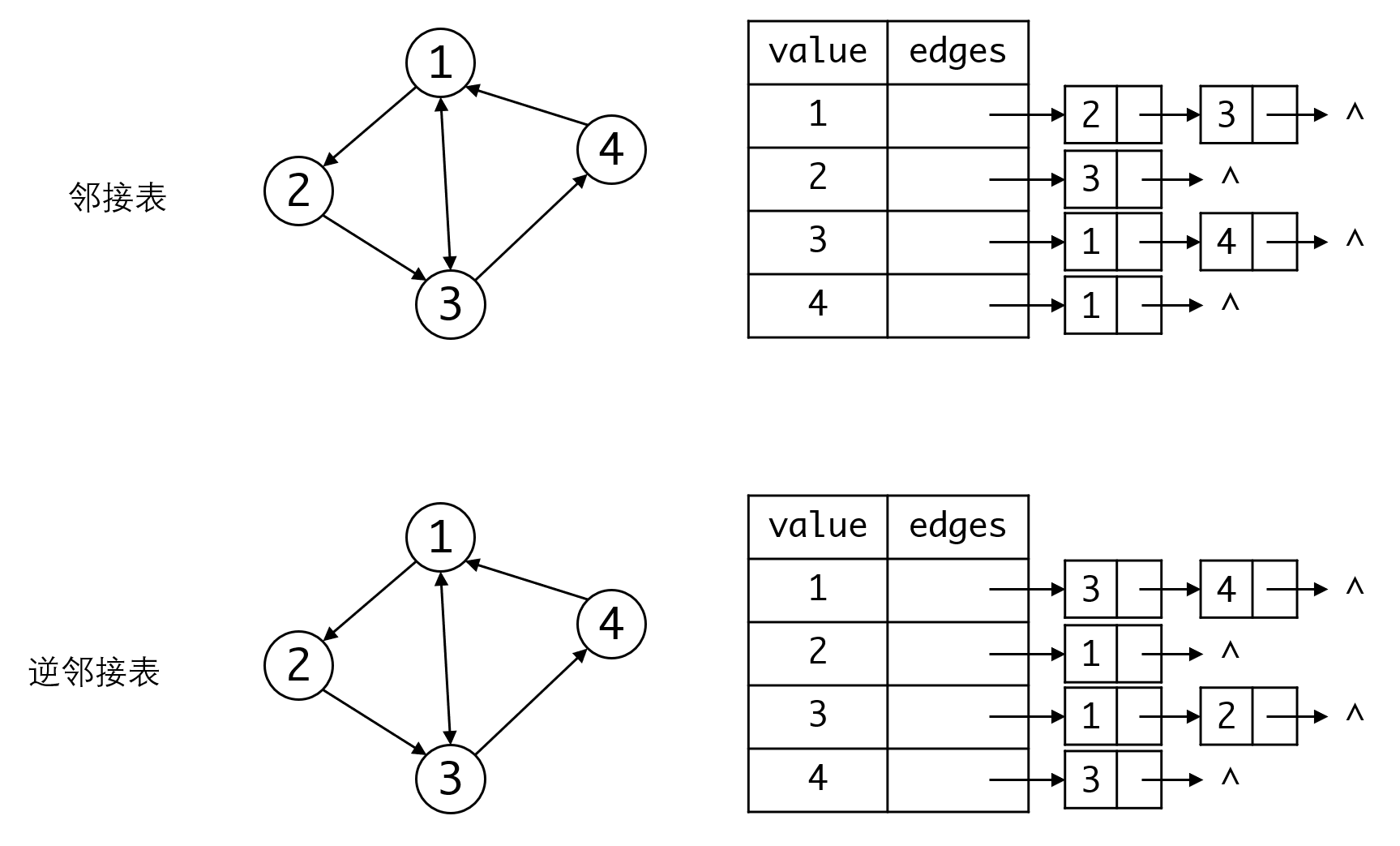
显然逆邻接表非常适合计算入度，计算出度则比较麻烦。

十字链表

既然邻接表和逆邻接表的优缺点正好互补，那么如果将两者结合起来，岂不美哉？

计算机科学家也是这么想的，这就是十字链表（Orthogonal List）。十字链表的边会记录对应的起点顶点和终点顶点，同时也要记录两个链表（同时属于两个链表）。假如某条边以顶点A起点，以B为终点。那么两个链表一个串联所有以A为起点的边，另一个串联所有以B为终点的边。同样的顶点也需要两个链表，一个是以该顶点为起点的所有边，一个是以该顶点为终点的所有边。

struct Vertex;

struct Edge{
    int value;
    Vertex* begin;    // 边的起点顶点
    Vertex* end;      // 边的终点顶点
    Edge*   in_next;  // 同起点边的链表
    Edge*   out_next; // 同终点边的链表
}

struct Vertex{
    int value;
    Edge* in;     // 入边链表
    Edge* out;    // 出边链表
}

十字链表的表示会有点乱，请大家仔细对照。

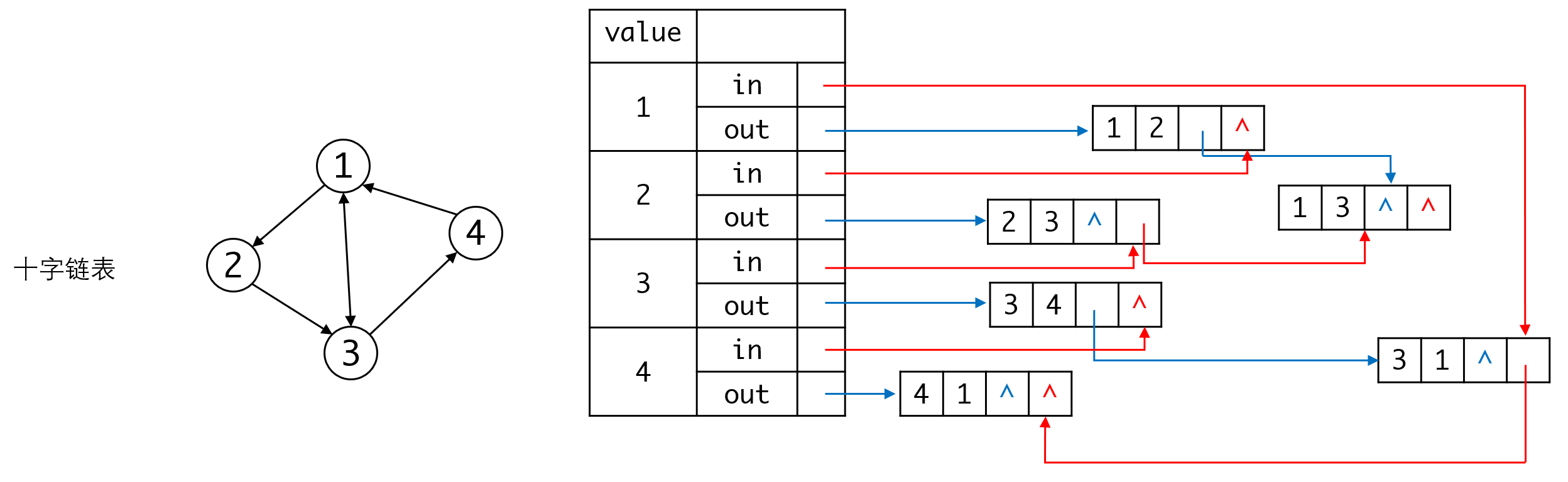
其中蓝色表示顶点的入边链表，红色表示出边链表。

十字链表这个译名其实有一定迷惑性，我们可以看出其实没有多少“十字”的感觉。Orthogonal实际应该解释成“正交”，比较形象地反应了整体结构的特点——每条边都记录了两个维度的信息。

十字链表不管求入度还是出度都很容易（复杂度是多少？）。不过跟双链表一样，空间开销更大了，整体的复杂度也增加了。

邻接多重表

对于无向图来说，邻接表也存在数据重复的问题：

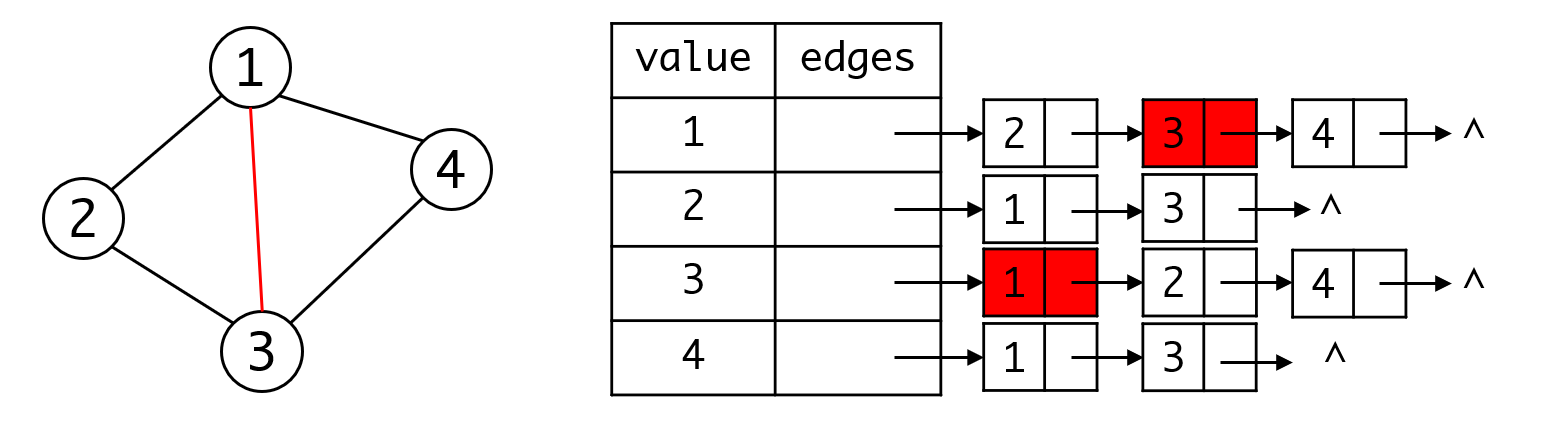
图中红色的这条线，在邻接表中实际上存在两个项，一个项是从1出发的链表，终点是3，另一个项是从3出发，终点是1。

在你处理边时，你需要将两个项目都进行处理才行。

要去掉重复的数据，方便我们处理，我们可以用邻接多重表来实现。

邻接多重表与十字链表类似，边上都要记录边对应的两个顶点。而对应的链表，则是串联与顶点有关的边：

struct Vertex;

struct Edge{
    int     value;
    Vertex* v1;
    Edge*   edge1;
    Vertex* v2;
    Edge*   edge2;
}

struct Vertex{
    int     value;
    Edge*   edges;
}

其中v1表示边的第一个顶点，链表edge1串联与v1相关的各条边。 同理v2表示边的第二个顶点，链表edge2串联与v2相关的各条边。

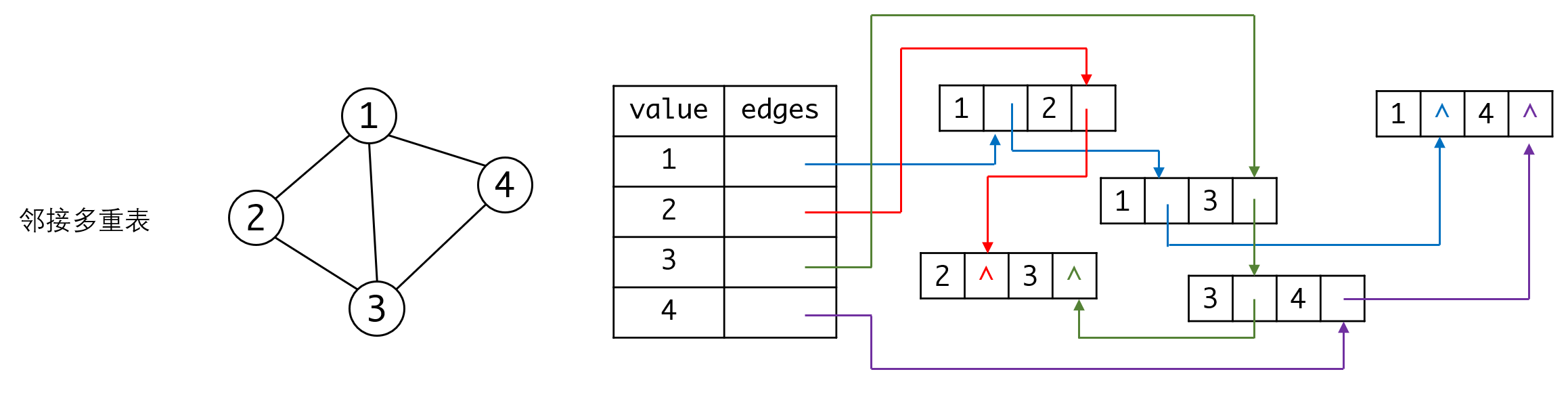
图中用不同颜色串联起不同顶点对应的边链表。从图中我们可以看出每条边只有一个边对象，操作不会再有重复项的问题。但和十字链表一样，多重链表处理的复杂度也大大提升了。