DAG及其应用
DAG及其应用
有向无环图(Directed Acycline Graph,DAG),顾名思义就是不含环的有向图。某种程度上DAG与树有一定相似性,他们都不会发生回溯,但DAG的有更高的灵活性。在实际工作中,DAG非常适合用来描述工程的行进过程。DAG算法也在这些领域有很好的应用。

拓扑排序
如果我们把上文的右图看作一个课程的依赖图。比如高数是电路的前置课程,而数据结构有两门前置课程,C语言和离散数学,组成原理也有两门前置课程,数字电路和C语言等等。
这种每个顶点都是一个活动,通过边表示活动的依赖关系的图,称为AOV(Activity on Vertex)。
那么我们很自然的有个要求,能否给出一个序列,按AOV网的要求完成所有课程的学习。这个序列称为拓扑排序。
拓扑排序的算法比较直观:从某个入度为0的顶点开始,从图中删除这个顶点,重复这一过程直到所有顶点都被删除。注意随着顶点被删除,边也被删除,原来无法进入排序的顶点可能因为入边被删除而入度变为0,从而可以进入排序。如果有向图不存在环,则最终一定可以删除所有顶点,我们看一个具体过程:
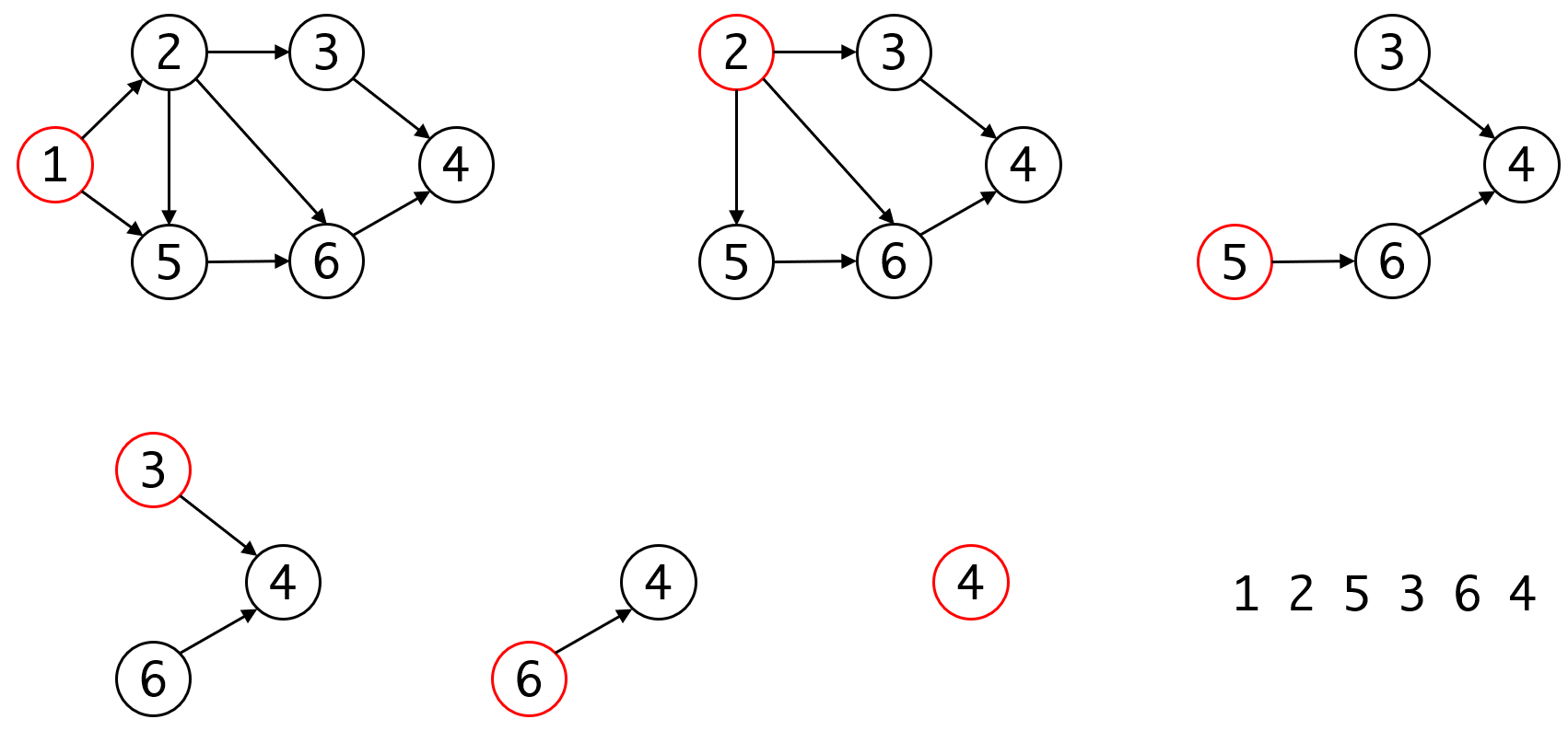
具体实现上,我们可以每回合查询所有入度为0的顶点,选择其中一个移除所有边,以下是伪代码:
vector<Vertex> topological_sort( Graph g ){
vector<Vertex> seq;
for( int i=0; i<g.vertecis_size(); ++i ){ // 每回合取一个元素
Vertex v = vertex_without_inedge(g); // 取一个没有入度的顶点
g.delete_vertex(v); // 从图中删除该顶点
seq.push_back(v); // 假如拓扑排序序列
}
}
思考一下
- 如果用邻接矩阵作为存储方式,要如何移除某个顶点(的所有出边)的操作?
- 邻接表、逆邻接表和十字链表,哪种更适合执行这个算法?
- 在邻接表里要如何实现移除某个顶点(的所有出边)的操作?
关键路径
AOV的活动在顶点上,边只体现依赖关系。但对于一个真实的工程项目,每个活动有不同的执行时间要求。对于这样的需求,我们一般用AOE(是Activity On Edge,不是Area of Effect)来表示。AOE图的顶点表示事件,或者你可以认为是成就、里程碑点、天赋技能等。而边才表示活动,一般我们用边的权表示活动的持续时间、或者开销。
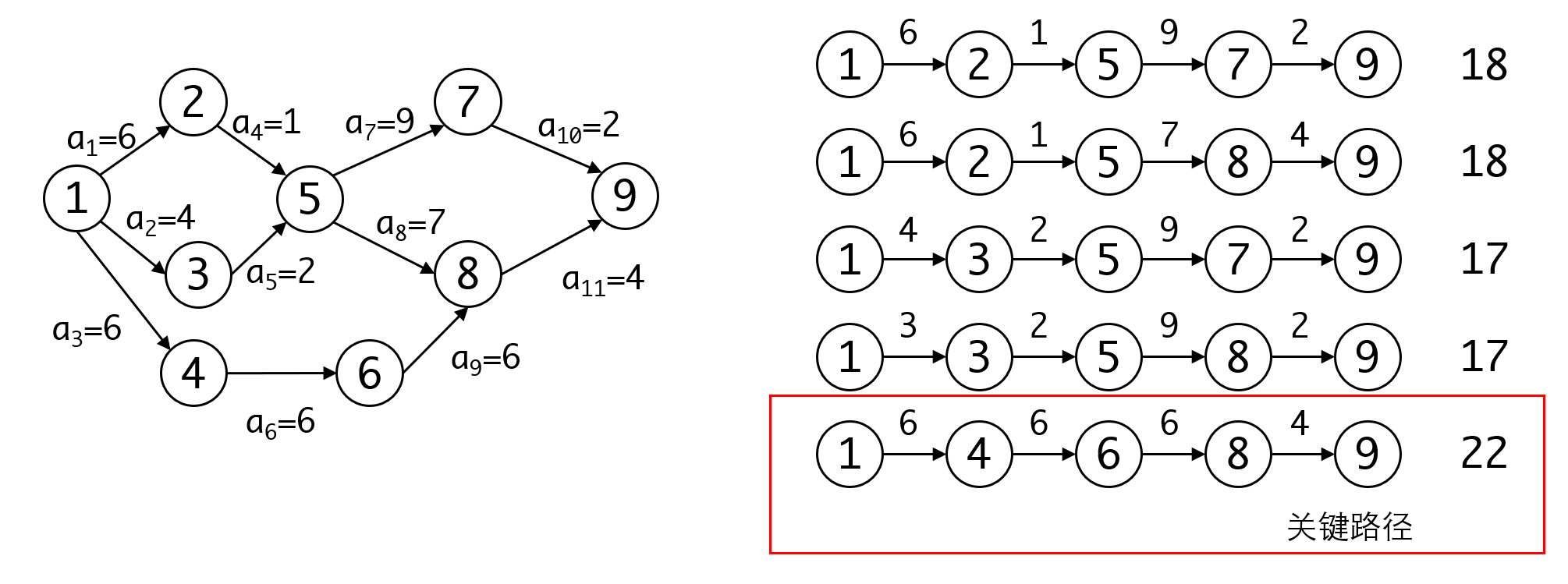
AOE图一般只有一个入度为0的点(开始)和一个出度为0的点(结束)。在开始和结束这两点间可能存在多条路径,所有这些路径中长度最长的路径,称为关键路径。之所以称为关键路径,是因为整个工程的完成时间不可能早于这条路径。同时这条路径上任何任务的延期,都会导致整体工程的延期。而缩短关键路径上相关任务的持续时间,则可能缩小整个工程的完成时间。
那么我们很自然的会有一个算法需求——给定一个AOE图,能否求出其关键路径?这是非常现实的要求。任意一个工程都希望知道影响自己最大的任务是哪些,你点天赋的时候,也会希望知道要如何投入才能最快地到达终极技能。
这个算法可以描述为:求每个顶点最早可以开始的时间和最晚必须开始的时间。如果某个顶点的和相同,说明这个顶点的事件既无法提前,也不能延后。那么该事件就处于关键路径上。
所以问题转化为:如何获得顶点的和。
我们以事件5为例:

事件5有两个前置操作(入边),分别从事件2和3发出。也就是说,要开始5,必须:
- 完成事件2,再经过时间为
1的活动。 - 完成事件3,再经过时间为
2的活动。
以上两个要求缺一不可,是与关系。如果我们我们把事件2的最早完成时间记作,把事件3的最早完成时间记作,那么事件5的完成时间必须不早于且不早于,也即两者的最大值:。这告诉我们顶点事件最早可以开始的时间,等于所有入边的权重加上对应起始顶点的最早开始时间。
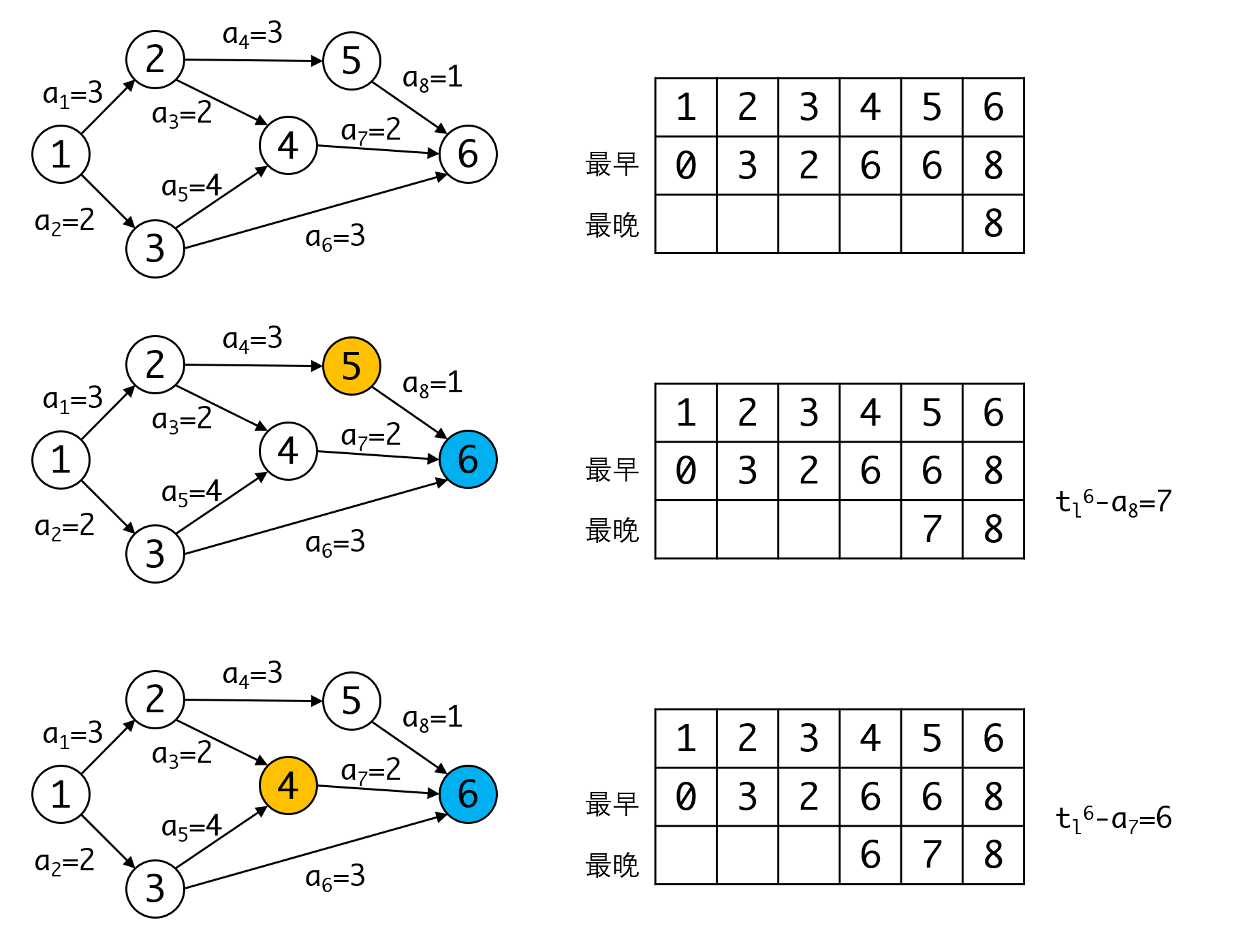
同理假如事件7和事件8的最晚完成时间不能晚于和。要满足这个要求,则事件5的最晚完成时间,不能晚于,也不能晚于。即取两者的最小值:。所以顶点事件最晚必须开始的事件,等于所有出边对应顶点的最晚开始事件减去边的权重。
有了这些理论基础,算法的流程就非常清楚了:
- 从起点开始计算每个顶点的最早开始时间。
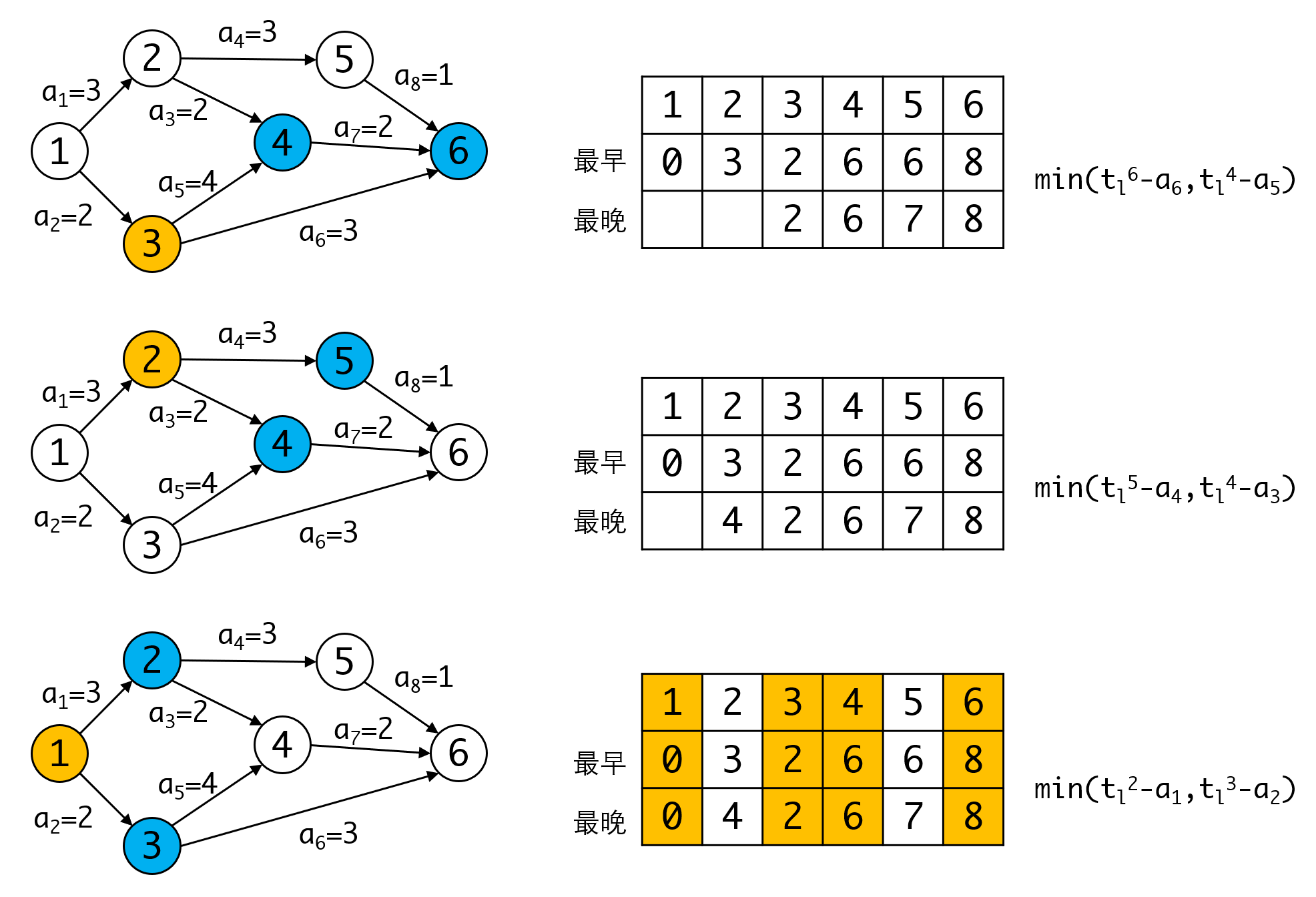
- 从结束点开始反推每个顶点的最晚开始时间。
对比两者,相同的顶点就是关键路径上的顶点。
为了保证计算某个顶点时,他的前置顶点都已经被计算。比如计算顶点5时,2和3的最早开始时间必须已经计算完毕。我们在开始前需要进行一次拓扑排序。计算最早开始时间时正向顺序计算,计算最晚结束时间时逆向顺序计算,就可以保证前置节点会预先计算。
我们看伪代码:
vector<Vertex> critical_path( Graph a ){
vector<Vertex> seq = topological_sort(a);
vector<int> e_time(a.vertex_size(),0); // 最早时间
for( Vertex v : seq ){
for( auto edge in a.in_edges(v) ){ // 查询每条入边
Vertex in_v = edge.get_begin(); // 边的开始顶点
int t = e_time[in_v]+edge.weight(); // 计算最早开始时间
e_time[v] = max(e_time[v], t); // 是所有边的最早开始时间的最大值
}
}
int finish_time = e_time[seq[a.vertex_size()-1]];
// 用整个图的结束时间初始化结束时间
vector<int> l_time(a.vertex_size(), finishe_time);
for( Vertex v : reverse(seq) ){ // 必须从后往前迭代
for( auto edge in a.out_edges(v) ){ // 查询每条出边
Vertex out_v = edge.get_end(); // 边的结束顶点
int t = l_time[out_v]-edge.weight(); // 计算最早开始时间
l_time[v] = min(l_time[v], t); // 是所有边的最晚开始时间的最小值
}
}
vector<Vertex> path;
for( Vertex v : seq ){
if( e_time[v] == l_time[v] )
path.push_back(v);
}
return path;
}
整个算法是比较复杂的,共分为三个部分,第一部分按拓扑排序的顺序计算最早开始时间,第二部分按拓扑排序的逆序计算最晚开始时间,最后按拓扑排序的顺序轮询顶点,两者相等的顶点则是关键路径上的顶点。
我们看一个完整的流程
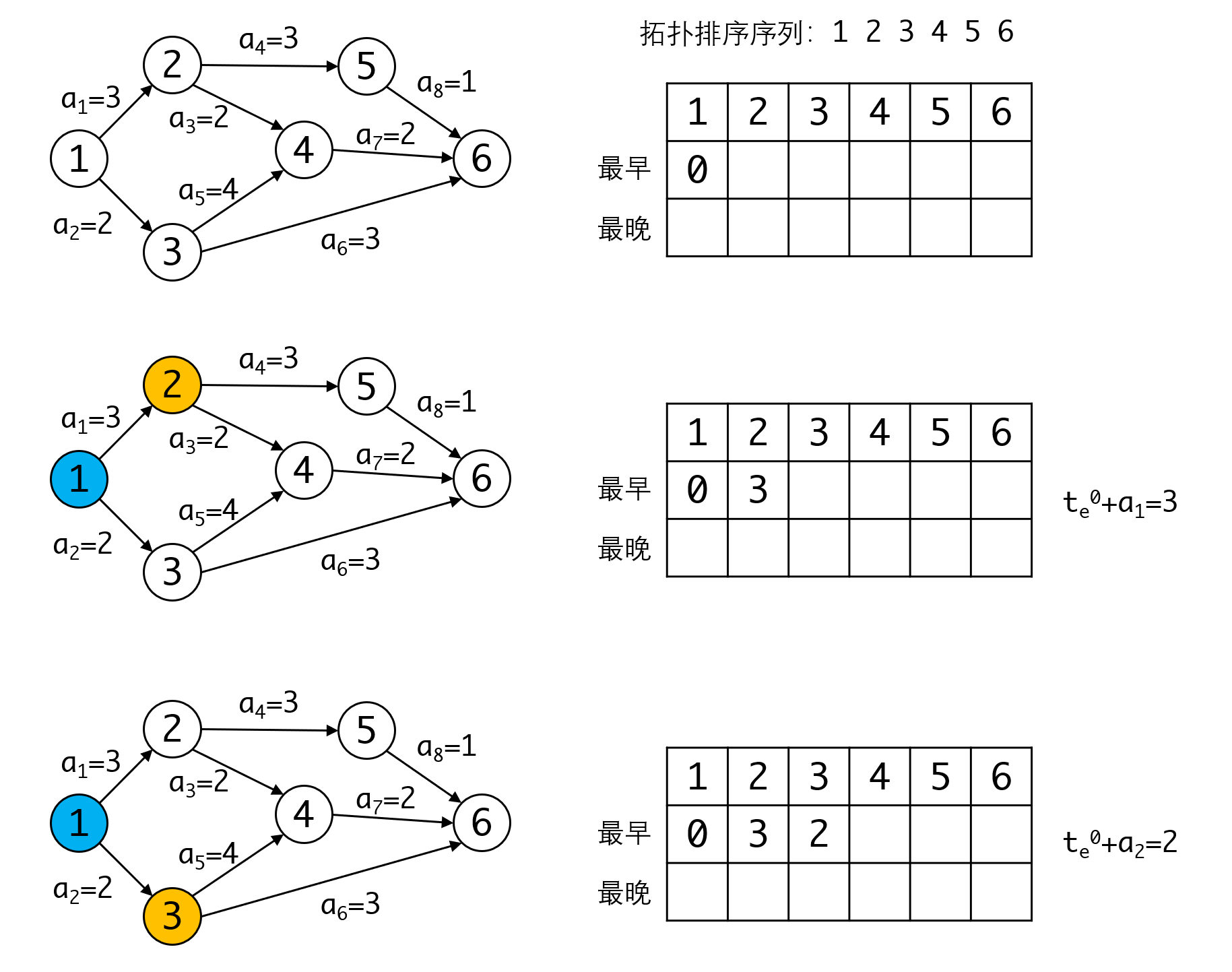
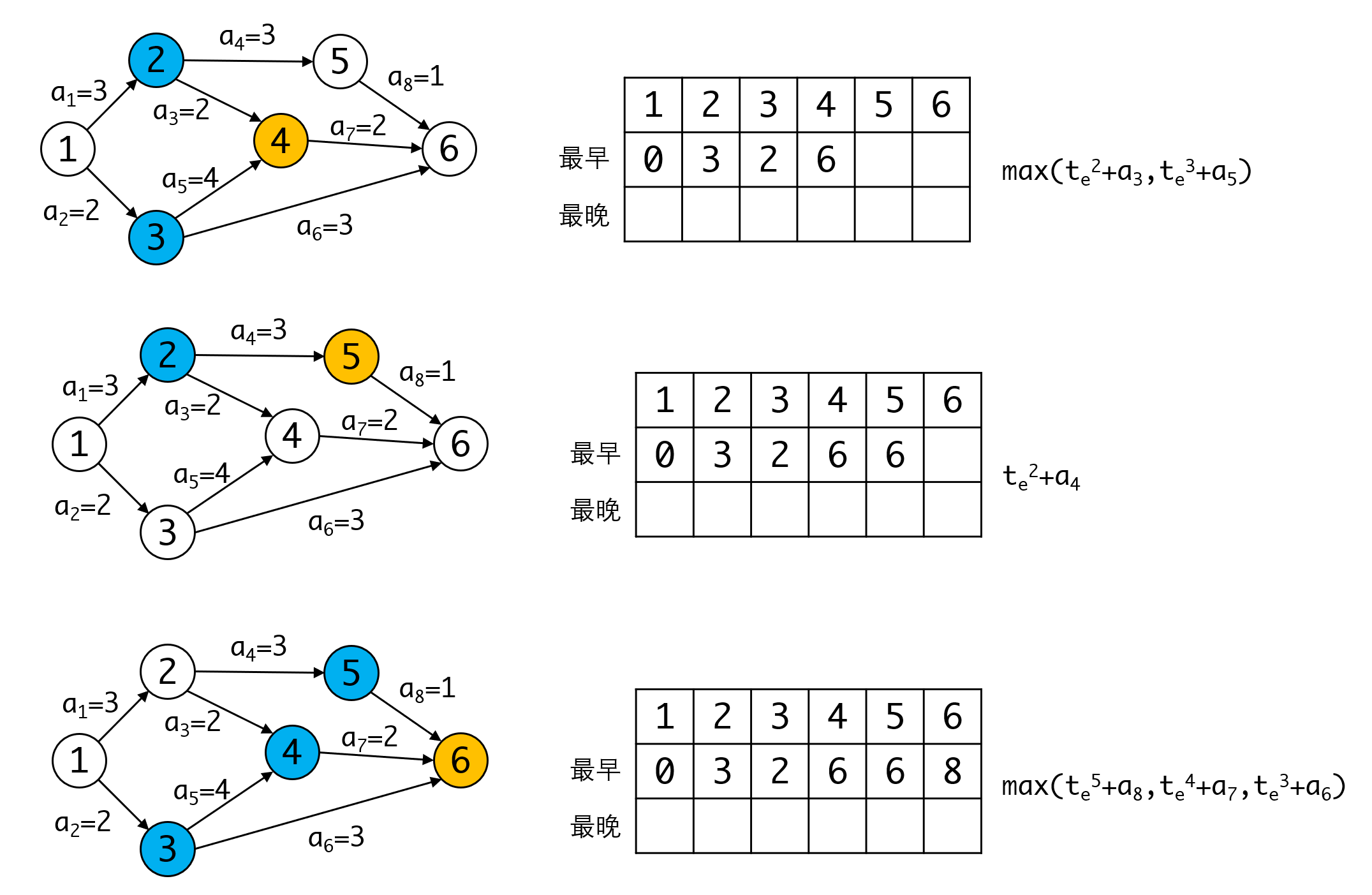
到这里我们正向计算完毕,求得整个工程的最早完成时间是8。接下来我们利用这个时间反推,看看要达到这个时间,每个事件的最晚发生事件不能晚于多少。
思考一下
AOE图可能包含多条关键路径吗?
假如一个AOE图有多条关键路径,那么上面的算法还有效吗?如果上面的算法不能满足要求,要如何改?