哈希表

问题的引入

我们已经学过基于两种数据结构构建的查找结构了，一种是顺序表，另一种是树。

顺序表要么可以达到$O(1)$的插入效率，但要付出$O(n)$的查找开销和删除开销；要么可以得到$O(logn)$的搜索效率，但要付出$O(n)$的插入和删除开销。

而树可以达到$O(logn)$的搜索、插入和删除开销，同时构建树表要付出额外的空间开销。

我们肯定会有这样的想法：有没有更快一点的数据结构来实现查找呢？这就是哈希表。

在介绍哈希表之前，我们先来看一个简化的模型，有助于我们理解哈希表：

如果有最多N个key的元素，并给你N个空间，要如何才能快速地实现元素的插入、删除和搜素呢？显然用数组来处理是最简单的：

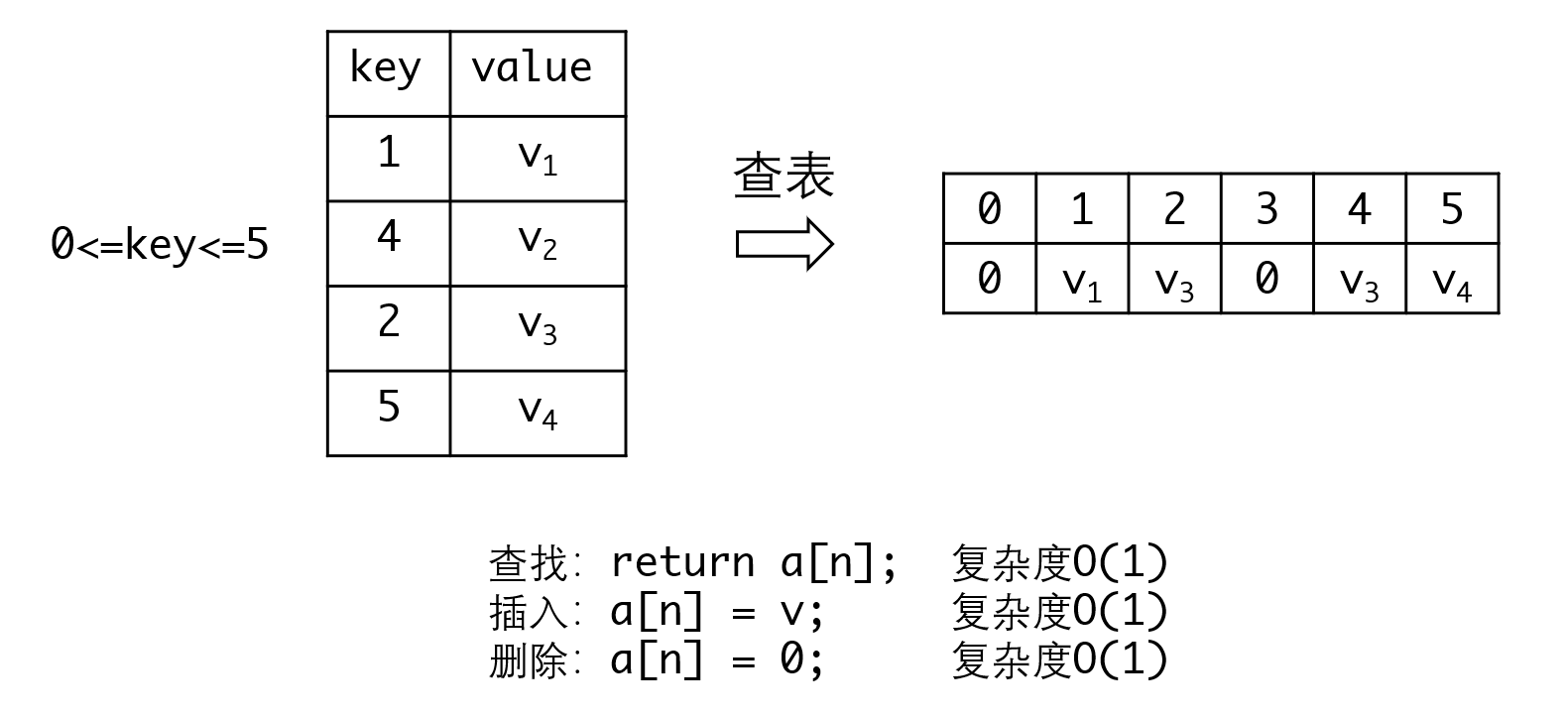
用数组可以让所有操作的复杂度达到$O(1)$。但问题也非常明显，如果数据分布非常不均匀，数组会造成很大的数据浪费：

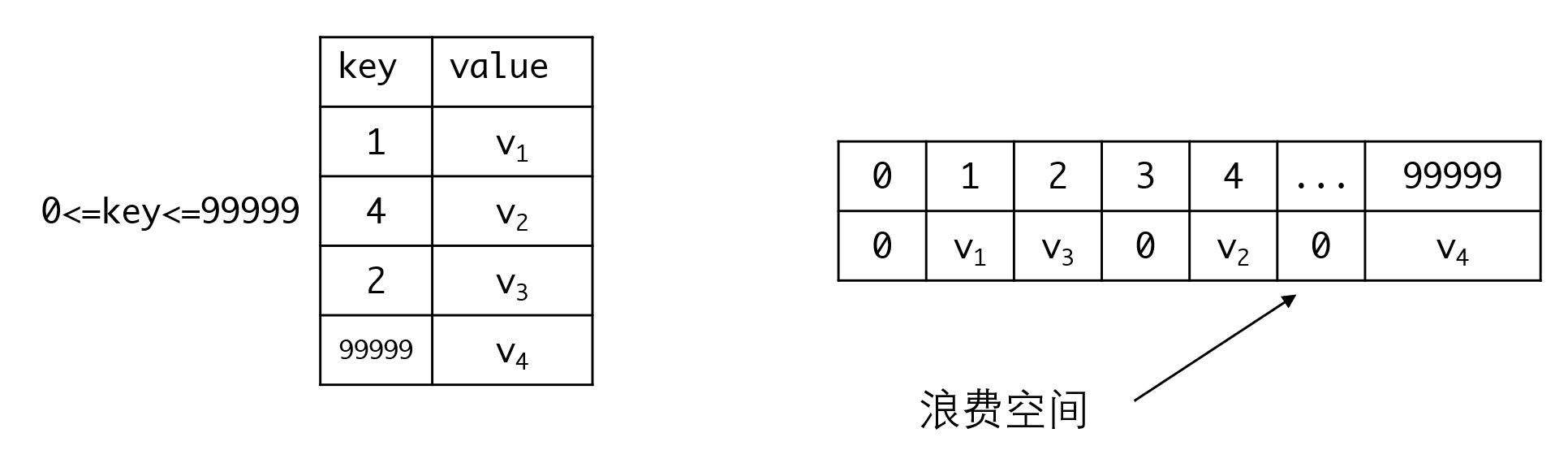
如图，中间从5~99998的空间都被浪费掉了，所以查表实际上是一种空间换时间的做法，这点应该在大一的数组学习中掌握了。

那么有没有办法把数组限制在一个比较小的范围内呢？我们可以用一个10个元素的数组来存放数据，然后我们取key%10作为查找的下标：

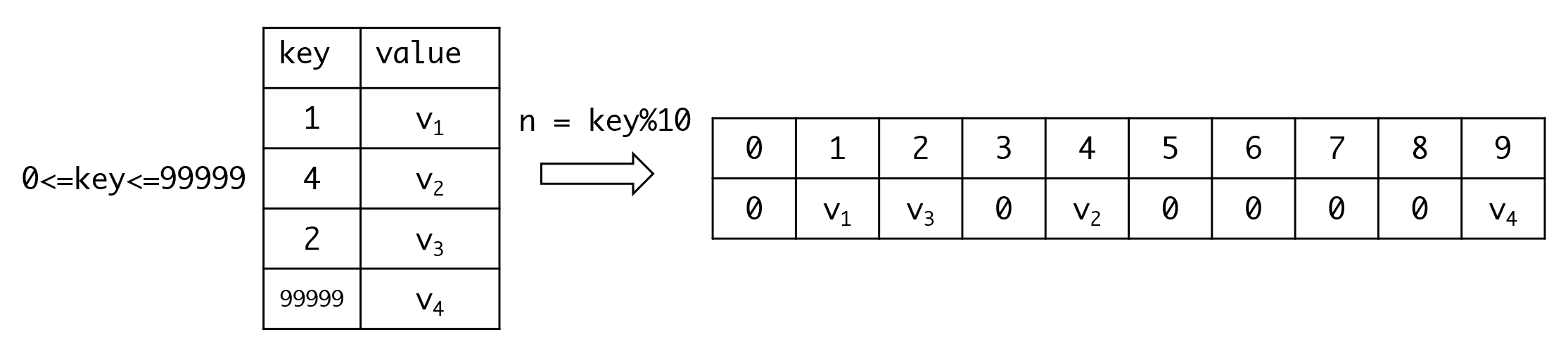
这样我们既把空间限制到一定范围，又保留了$O(1)$的操作时间复杂度。这种数据结构称为哈希表（Hash Table），也称散列表。我们把$hash(key) = key \mod 10$这个操作称为哈希函数。

聪明的同学一定想到了如果我如果有4、14、24...这些key，岂不是要塞进同一个空间了？ 没错，因为哈希表是一种多对一的映射，冲突是无法避免的。但我们可以通过一些方法来尽量避免这种冲突的出现，这就是我们这节要讨论的问题。

哈希函数

哈希函数可以说是哈希表的灵魂，决定了哈希表元素的布局。但哈希函数并不止在哈希表上应用，实际上他在数据库、数字签名、安全验证等方面都有着非常广泛的应用，对他的研究也是信息安全的一大重要领域。前几年非常热的数字加密货币技术也以哈希计算为基础的。

如果单从哈希表的角度出发，一个好的哈希函数至少要满足以下两点：

1. 计算速度快
2. 防碰撞效果好

这两个要求都是出于效率的考虑，如果哈希函数计算非常慢，每次查表都要消耗大量的时间，那么使用哈希表就会变得非常不经济。而如果防碰撞效果不好，可能导致数据聚集在某个范围内，增加碰撞处理，从而增加时间开销。

基于第一个要求，一般哈希函数只应当包含简单的加减乘除和位运算。而第二个要求则要求函数的输出结果要分布平均，并且有较强的随机性。

取余数法

这是最容易想到的哈希函数，就如上面例子里给出的，如果开辟了长度为L的空间，那么我们可以取hash(key) = key%L作为哈希函数。这种函数显然符合第一个要求。单对于第二个要求则不然，取余数法的结果对于随机分布的key分布平均，但如果key具有一定的规律性，则会加剧冲突的概率，这个问题使得L的选择要比较小心——一般来说我们都会选质数。

为什么要选素数

一个显而易见的结论是，如果key是以L为距离的等差数列，那么所有哈希函数的结果都会相等。例如：如果选L=7，那么2 9 16 23 ....这样的key序列得到的结果都是2，这意味着他们都会发生冲突。对于质数来说，这是唯一会造成数据聚集的情况，在其他情况下，数据都会均匀分布。

但对于和数则不然，如果我们选L=6，对于距离为2和3（6的质因数）的等差数列来说，他们只会占用某些下标，而跳过其他的下标：对于0 2 4 6 8 10的序列，只占用0 2 4这三个格子，而对于0 3 6 9，更是只占用0和3这两个格子。也就是说L的每个质因子都会造成分布的不均匀。

这就是为什么我们会选择质数作为L的原因。

但取余数法依然有其他问题，例如他的分布不够随机，相邻key的结果通常也是相邻（对一些解决冲突的方案不友好）等等。但取余数的计算简单，同时又可以明确地将范围限制到L的范围。所以取余数法一般作为最后一道防线使用，我们会先使用其他方式计算哈希值，最后再取余数，得到最后的结果。

折叠法

折叠法是将key分成几段，再通过一定的运算拼接起来：

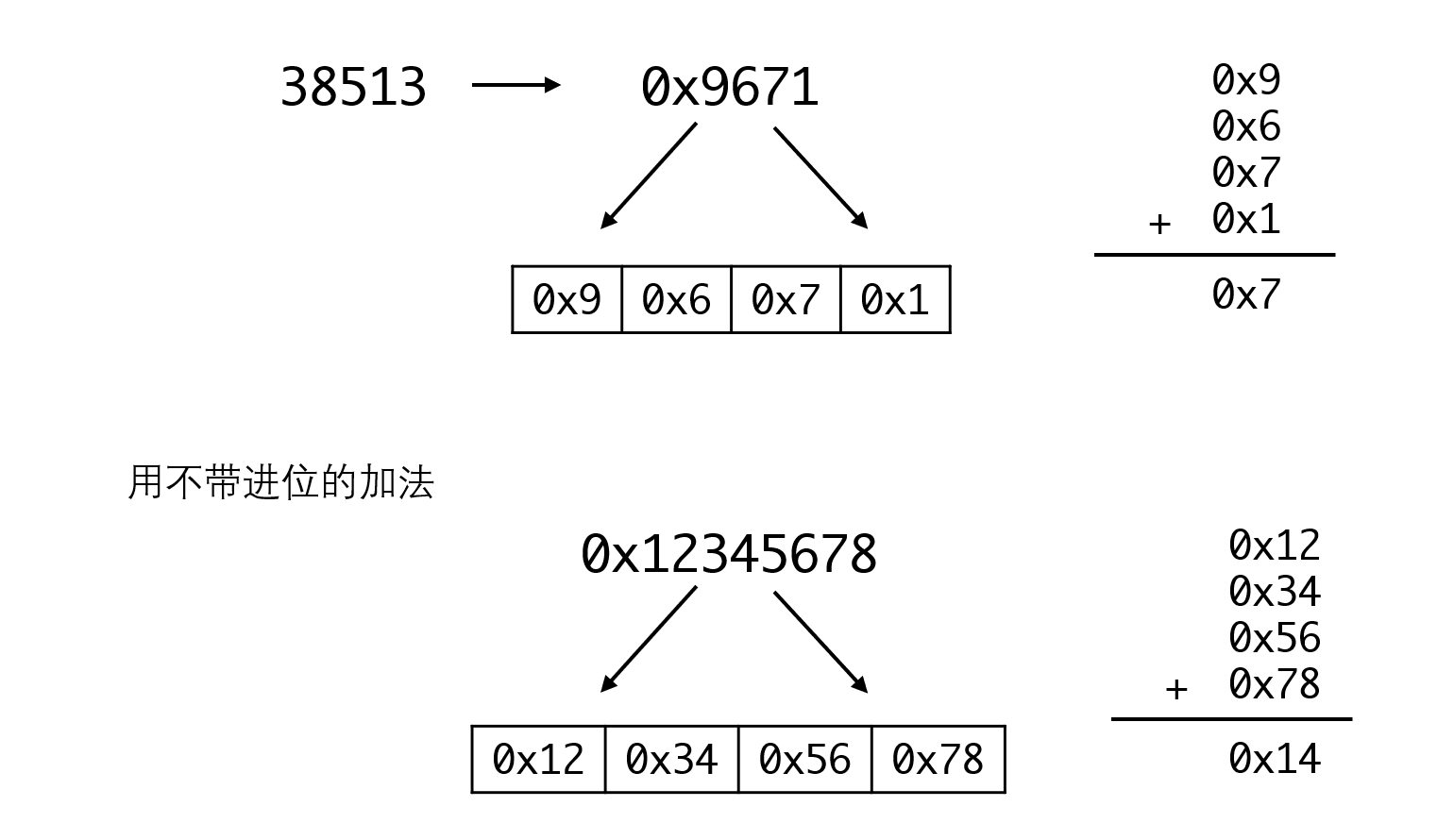
例如对于38513这个key，我们先转为16进制0x9671，然后拆成四个4位整数：0x9，0x6，0x7和0x1。再将这四个数相加（舍去进位，只保留低位），得到的结果0x7就是对应哈希函数的结果。

更复杂一点，我们也可以8位一拆，像下面的0x12345678，拆成0x12、0x34、0x56和0x78，再用不带进位的加法相加，得到的0x14就是结果。

折叠法中出了加减这些操作，更常用的是按位异或的方式，所谓异或是当两个位相等时，得到0，两个位不等时，得到1，对应的真值表如下：

	1	0
1	0	1
0	1	0

以上面的0x9671为例：

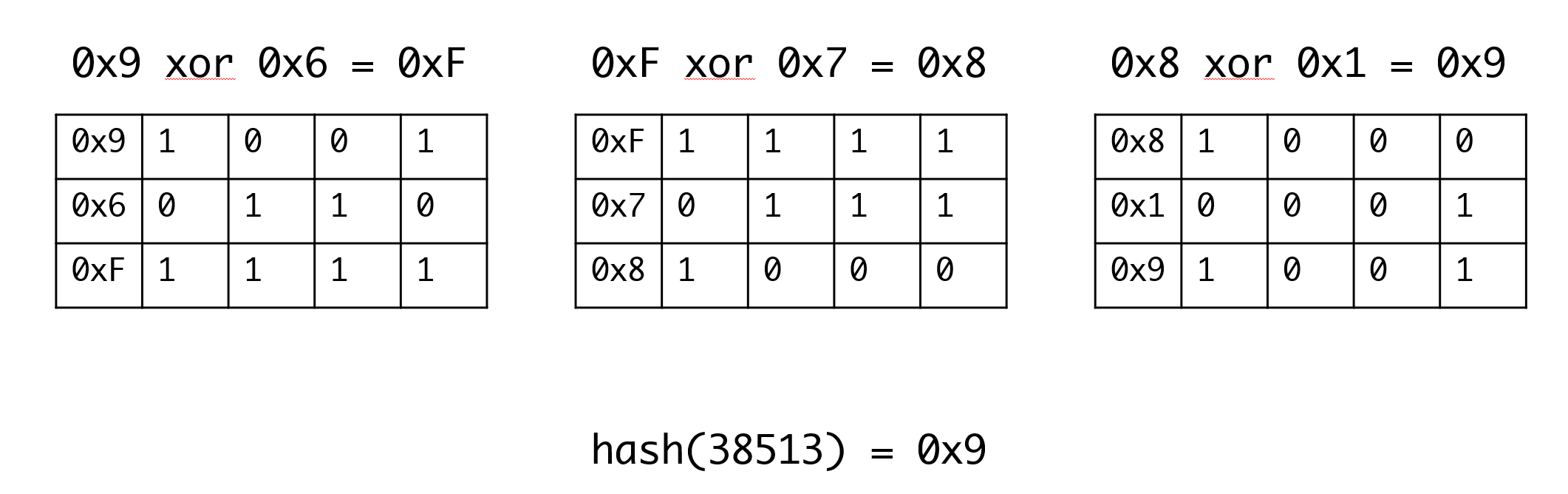
异或操作是大多数CPU都内建的指令，因此这种运算与加法运算的效率基本相当，同时异或操作xor结果的随机性很强，通常认为这是一种非常好的方式。

伪随机数法

我们先看这段代码：

#include <iostream>
#include <cstdlib>

using namespace std;

int main(){
    srand(1000);
    for( int i=0; i<10; ++i ){
        printf("%d\n", rand());
    }
    return 0;
}

如果你运行这段代码，会发现每次运行的结果都是一样的。因为库函数的随机数是伪随机。在种子（即srand函数的参数）确定的情况下，将会生成相同的序列。我们可以利用这一特点，令hash(key)为指定种子的第key个随机数序列。

用随机函数作为哈希函数的好处在于他的结果是足够平均的。但缺点也很明显，不同的key的运算时间是不同的，当key非常大时有可能效率非常低。

其他方法

例如取key中的某一些位来作为哈希key，比如如果key的范围很大，那么我们可以取第1 3 5 7等位置构成需要的哈希key。

又或者平方取中法，可以将key平方之后，取中间的某些位数构成哈希key。

等等等等，总之要注意哈希函数的两个要求：1. 容易计算。2. 有充分的随机性。

实际工作中最常用的还是取余数和折叠法，或者这两者的结合：先折叠，再取余数。

冲突解决

即使我们非常小心地选择哈希函数，冲突依然是不可避免的。所以冲突处理是哈希表不可缺少的策略设计，我们只讨论两种比较常见的冲突处理策略：

链地址法

链地址法非常好理解，表中的每个元素都是链表的头指针，真实的数据存放于链表中。当发生冲突时，相同哈希key的值被放置于链表中组织起来，从而避免了冲突的发生：

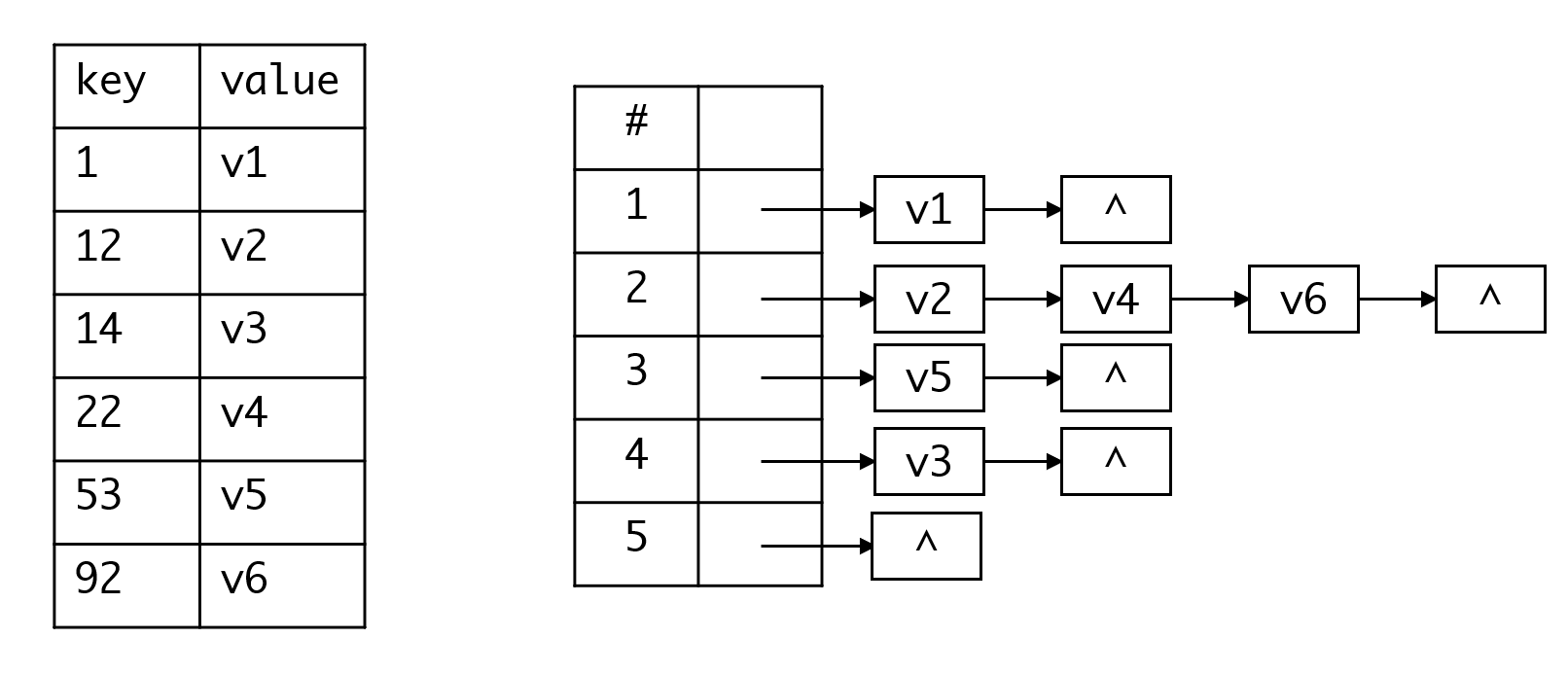
开放定址法

开放定址法不使用链表来处理冲突，而是在表里寻找有没有多余的空间来放置：

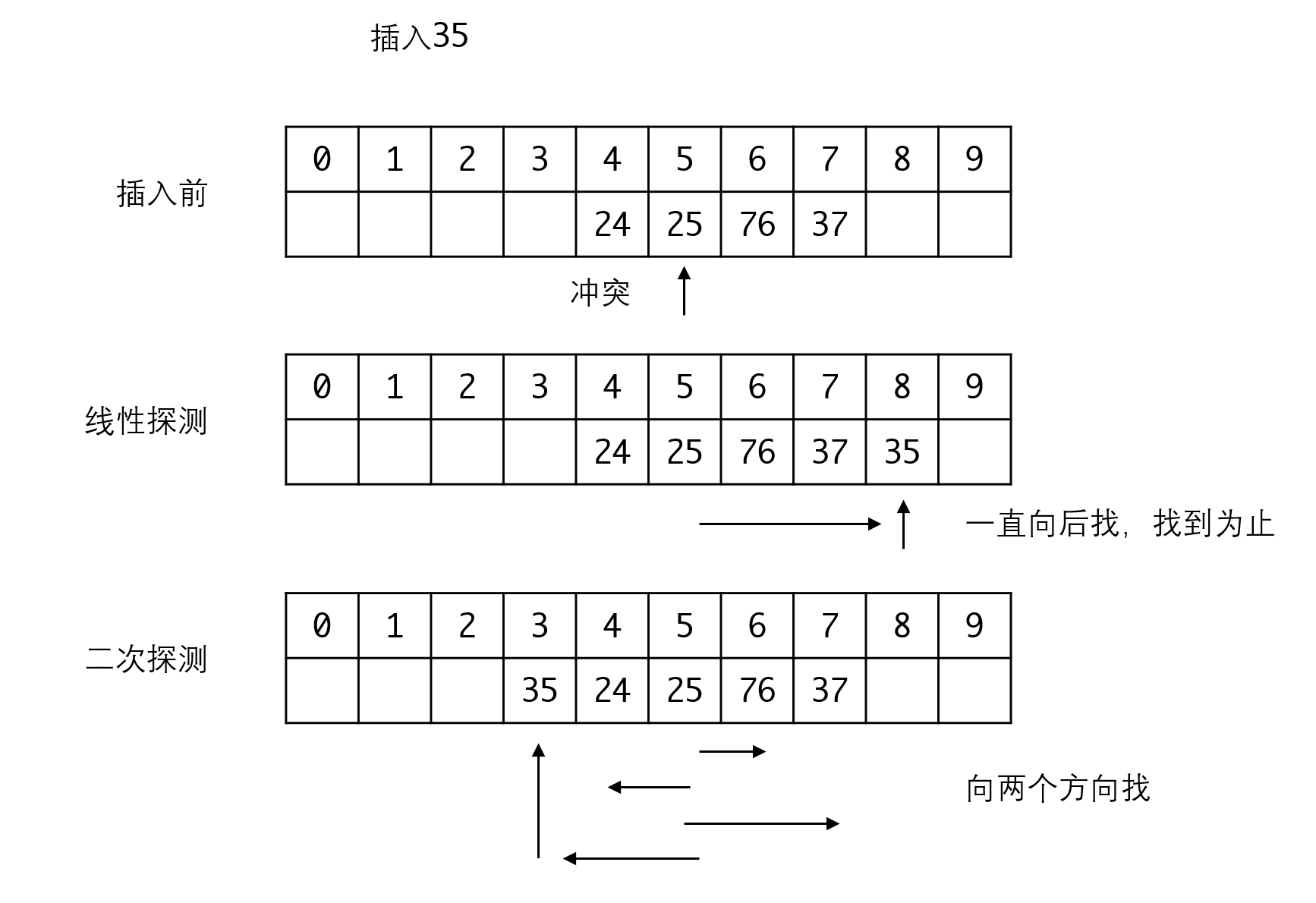
开放定址法还有不同的处理策略。例如线性探测策略：从当前位置向后找，直到找到第一个空格为止。这种策略会导致数据一直向后面堆积。为此可以引入二次探测，在两个方向搜索，一次向后搜索，一次向前搜索。

开放定址法还可以使用随机函数或者随机再哈希函数等策略来执行，总之就是在原有的表里找空间存放。

开放定址的数据结构较链地址简单，但他最大的问题是会造成所谓的“二次聚集”问题，例如上面线性探测法中，新来的哈希值是4、5、6、7、8的元素，都会竞争9这个位置。这种情况会加重冲突的情况。

另外一个很严重的问题是当我们删除某个key时，可能导致搜索链条的失效。

还是以线性探测法为例，如果我们删除76，当我们搜索35时，第一次我们找到25，发现冲突，此时按线性探测法就应当向后找。但由于此时76已被删除，程序可能会误认为表中不存在35而导致搜索失败。

实际应用中，我们一般还是使用链地址法来处理。

哈希表与搜索树

我们已经学习了两类典型为搜索设计的数据结构——搜索树和哈希表，这两类数据结构也是行业里应用最广泛的两种数据结构。大多数的语言和库，都提供这两者的实现。

你知道吗？

你知道C++ STL和Java里实现的这两类的数据结构分别是什么吗？

那么我们应该如何选择呢？他们同时存在也就说明他们有着对方无法取代的优点，同时也有着无法取代对方的缺陷。

搜索树所有操作的复杂度都是$O(logn)$，每个节点要消耗多余的空间。哈希表的操作复杂度是$O(1)$，节点不消耗多余空间，但需要预分配空间。

我们可以这么看，搜索树是一种上限较低，但下限较高的数据结构，他很稳定，不论数据如何分布，都可以提供给你不高于$O(logn)$的操作。

而哈希表的下限就低多了，设想一下，假如我们用链地址法，同时所有的元素都冲突了，那么很明显，哈希表就退化到链表：

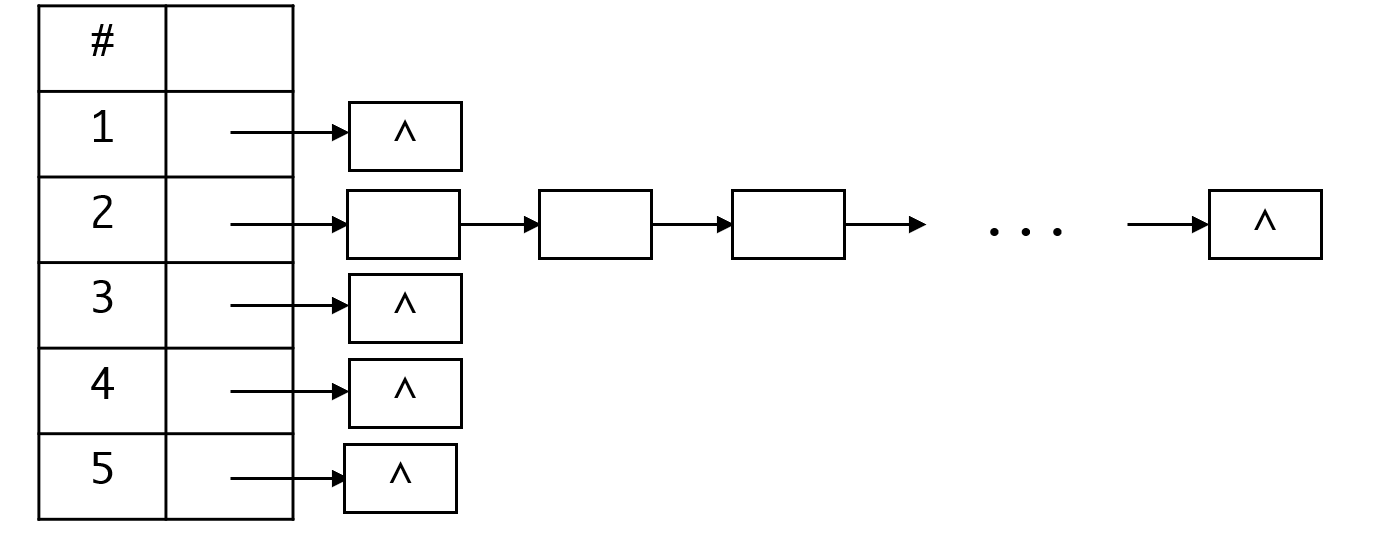
更要命的是，我们对这种情况无法预防，我们可以通过设计良好的哈希函数来尽量减少这一情况的发生概率，但我们无法完全避免他。

因此哈希表在较为极端的情况下效率会远远低于搜索树。但他又有着相当好的平均复杂度：$O(1)$，真是让人又爱又恨。

在大多数场合，哈希表都是非常有效的工具，不过我们也需要知道他的局限性。