并查集

并查集是一种多叉树，他非常适合解决分组或者归类的问题。

具体来说，并查集通过合并不同集合来达到类似聚类的目的。而每次查询都会执行路径压缩，使下一次查询更有效率。

这里标为黑色的三个关键词中，合并和查询是并查集的基本操作。而路径压缩则是并查集高效的主要途径。

这里有个非常清晰且形象生动的说明，对你理解并查集会非常有帮助。本节内容也是依据这个笔记编写的。

引入

我们看一个非常非常典型的题目：

亲戚（洛谷P1551）

亲戚

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：$x$ 和 $y$ 是亲戚，$y$ 和 $z$ 是亲戚，那么 $x$ 和 $z$ 也是亲戚。如果 $x$，$y$ 是亲戚，那么 $x$ 的亲戚都是 $y$ 的亲戚，$y$ 的亲戚也都是 $x$ 的亲戚。

输入格式

第一行：三个整数 $n,m,p$，（$n,m,p \le 5000$），分别表示有 $n$ 个人，$m$ 个亲戚关系，询问 $p$ 对亲戚关系。

以下 $m$ 行：每行两个数 $M_i$，$M_j$，$1 \le M_i,~M_j\le N$，表示 $M_i$ 和 $M_j$ 具有亲戚关系。

接下来 $p$ 行：每行两个数 $P_i,P_j$，询问 $P_i$ 和 $P_j$ 是否具有亲戚关系。

输出格式

$p$ 行，每行一个 Yes 或 No。表示第 $i$ 个询问的答案为“具有”或“不具有”亲戚关系。

你可以把这个问题看作一个分类，或者聚类问题。最终属于同一个集合的元素都会被聚合在一起。如果你玩过前两年非常火的合并大西瓜的话，合并的过程是非常相似的。

首先我们规定，每个集合都有一个代表元素，就像每个家族都有一个族长那样（注意这里的族长只有代表的含义，并不意味着元素之间有从属关系）。

那么初始状态下，此时尚没有元素合并到同一个集合，因此我们有N个集合，每个集合只有一个元素。那么每个集合的元素的代表元素就是这个唯一的元素。

我们用一个箭头表示代表关系，如果一个元素不是代表元素，那么箭头指向的元素会替他代表，直至到代表元素为自己的元素为止，因此一开始的情况如图：

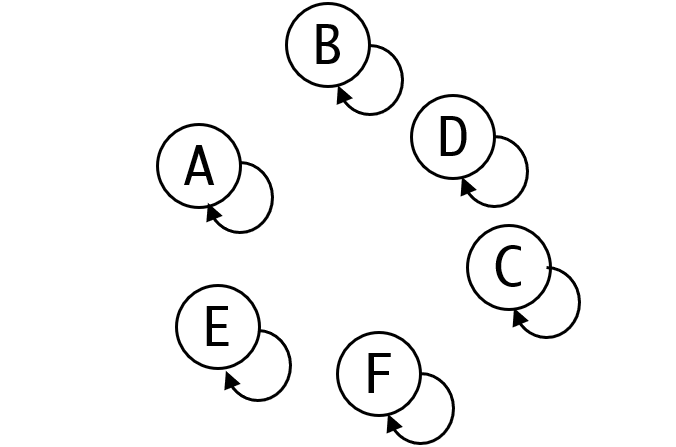
注意，这里我们将箭头指向自己是为了方便判断元素是否为代表元素。当然，指向空，或者-1之类的非常规值也是可以的。

构建

合并集合，就由这个集合的代表元素将代表权指向另一个集合的代表元素。这句话可能有点绕，我们来看下合并的过程：

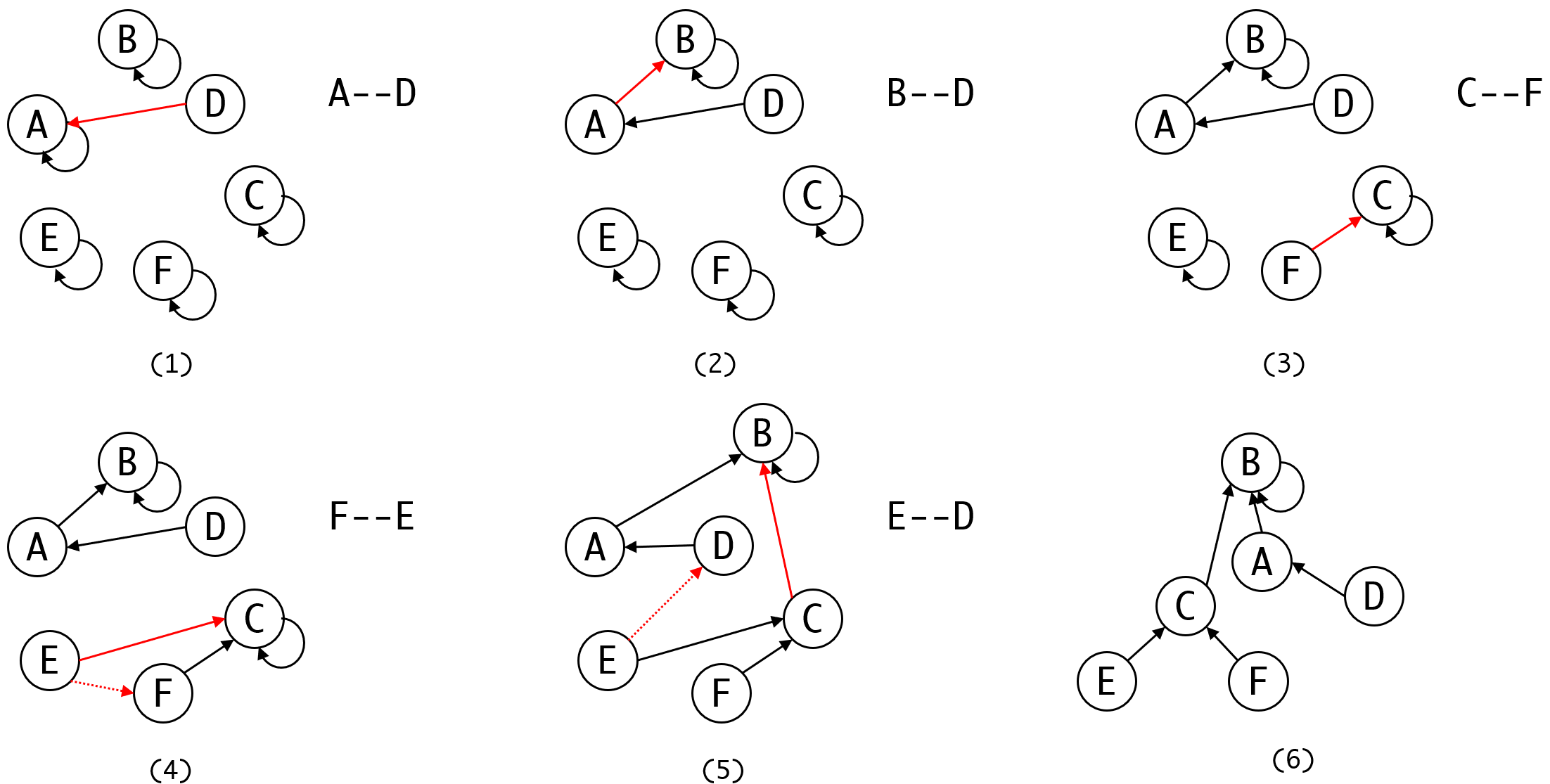
每一次我们读到元素之间的关系，我们就可能会进行一次集合的合并。

途中红色的线表示本回合建立的联系，其中虚线表示读取到的联系，实线表示实际建立的联系。

第一回合的合并简单明了，集合[A]和[D]合并，我们令[D]并入[A]。令集合[D]的代表元素D（请注意集合和元素的区别）失去代表集合的权力，由A来替他代表这个集合。所以我们得到一个新集合，有两个元素，代表元素是A。

注意，操作是把把元素所在集合的代表元素指向另一个元素所在集合的代表元素。这意味操作都在集合的代表元素中进行，而不是简单地把这个元素的代表指向新元素。

这在(2)里体现的非常明显，B和D之间有关联，我们让D所在的集合并入B，所以我们需要找到D所在集合的代表元素，也就是A，然后令A指向B的代表元素也就是B本身，由B来代表新的集合。

剩下的流程中，注意（4）和（5）这两步，当E合并F时，我们不是直接把E指向F，而是要指向F的代表节点，也就是C。

同样的当E指向D时，联系并不是在E和D之间建立，而是让E的代表元素C，指向D的代表元素B。再次强调，操作都在集合的代表元素之间进行。

在这个结构下，要判断两个节点是否属于同一个结合，只需要判断他们所在集合的代表元素是否时同一个即可。

代码实现

操作原型

struct DisjSet{
    vector<int> fa;
    DisjSet( int size );  // 初始化
    int find( int v );    // 搜索
    void merge( int v1, int v2 ); // 合并
};

整个操作很简单，一共有3个函数来完成。分别是初始化、查找和合并。fa（father）表示代表元素的指向。例如fa[i]=j，表示id为i的元素的代表元素是j。

初始化

DisjSet::DisjSet( int size ){
    fa.resize(size);
    for( int i=0; i<size; ++i){
        fa[i] = i;     // 初始各个集合只有一个元素，代表元素就是该元素
    }
}

初始化时，分配空间并为每个元素（集合）赋初值，此时他们都指向自己，所以共有n个集合。

搜索

int DisjSet::find( int v ){
    if( fa[v] == v )
        return v;
    else
        return find(fa[v]);
}

如果指向自己，说明自己就是代表元素。否则就需要往前找。

这里我们用递归来做，当然也可以用递推式，不过递归代码量少，直观。而且对下面路径压缩的实现会非常有好处。

合并

void DisjSet::merge( int v1, int v2 ){
    fa[find(v2)] = find(v1); // v2集合的代表节点接到v1集合的代表节点上
}

路径压缩

我们设想一个比较坏的情况：

E--F
D--F
C--F
B--F
A--F

这样的关系构建之后，就会变成一整条链：

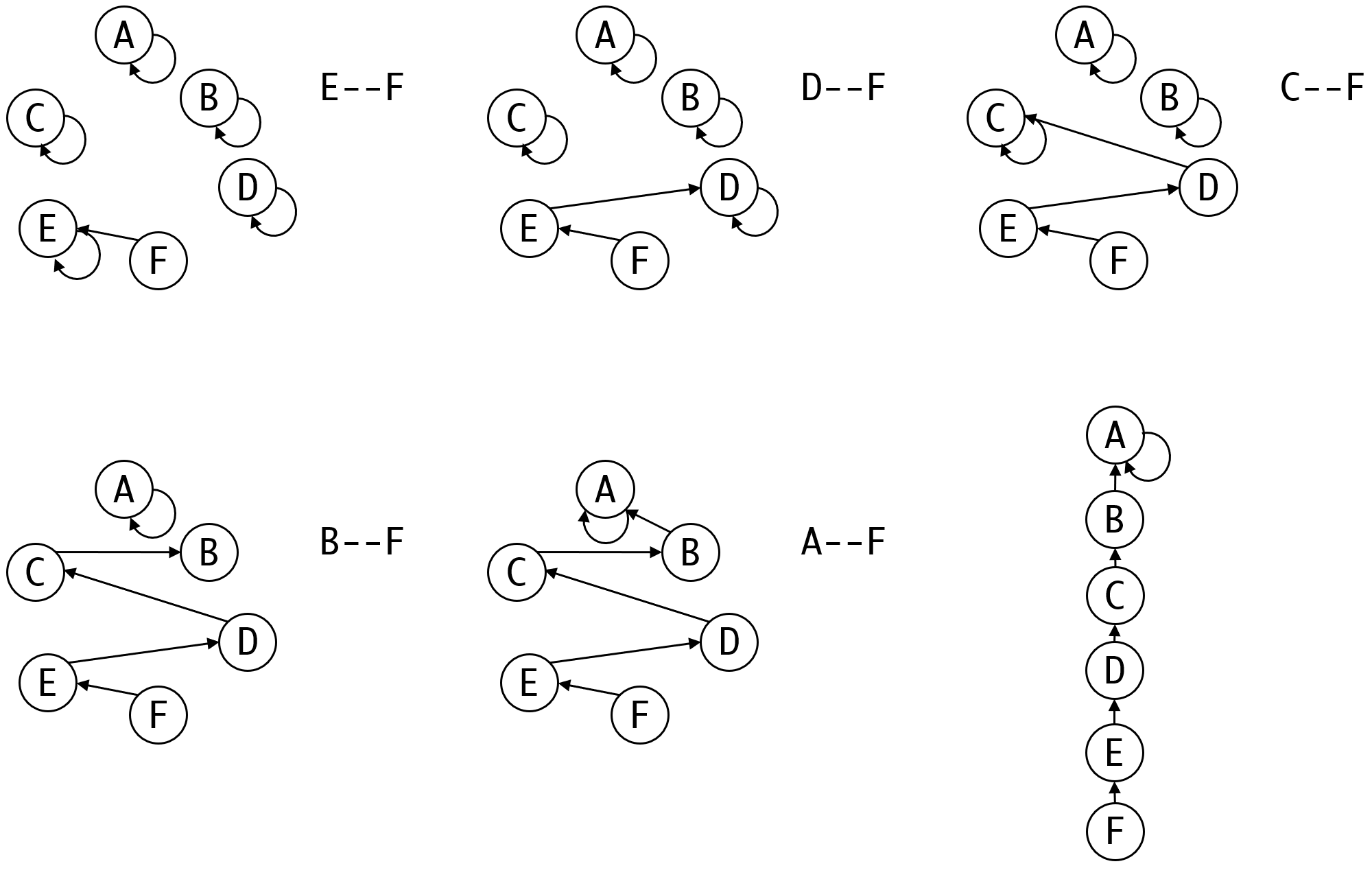
显然这种结构的效率很低。

如果观察我们的搜索的过程，我们可以发现我们每次都要遍历整条链上的所有元素。而实际上，遍历过的整条链上的所有元素都可以直接挂到代表元素上：

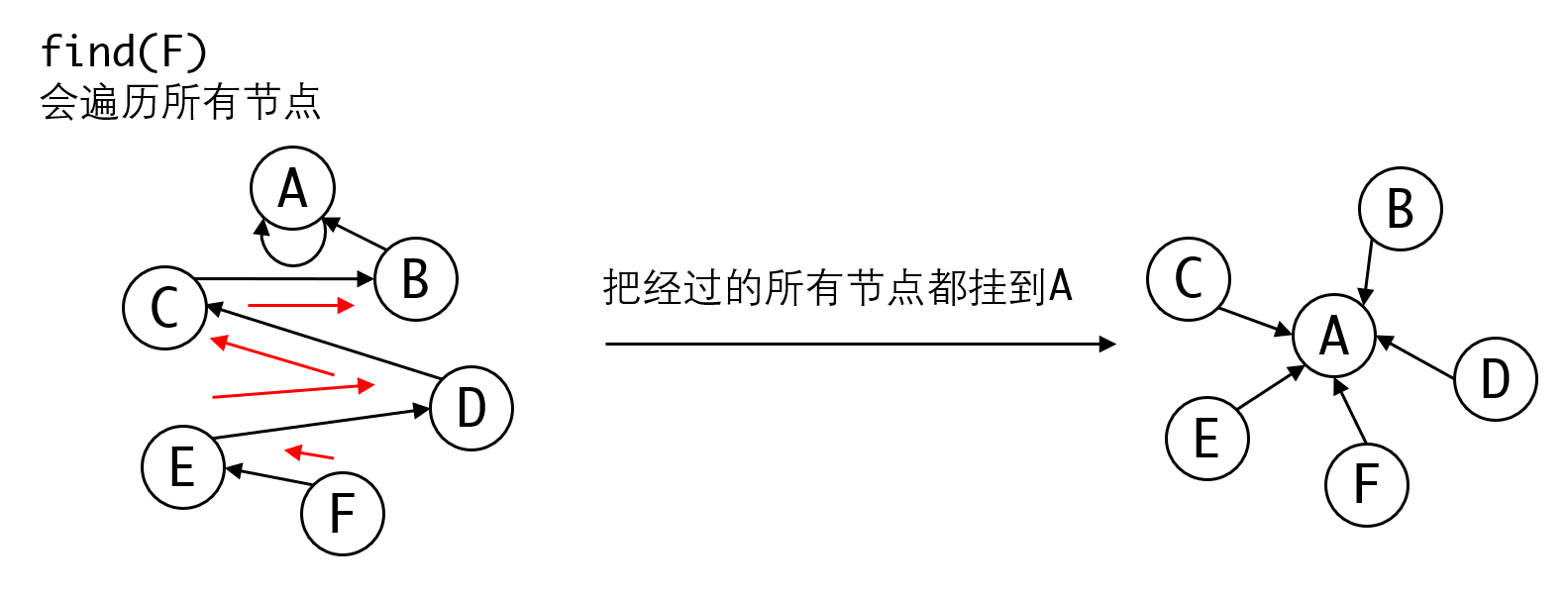
这种“菊花图”（非常形象）显然是我们所能得到的最好的结果了。

这种做法巧妙地把优化隐含在每次搜索中，每一次搜索都会令整体结构变得更优。更妙的是，由于我们的查找算法是递归算法，在递归返回的时候，可以自然地得到本元素的代表元素。所以把经过的节点挂上去，也不过是多一条语句的问题，基本不增加任何开销：

int DisjSet::find( int v ){
    if( fa[v] == v )
        return v;
    else{
        fa[v] = find(fa[v])
        return fa[v];
    }
}

这个代码还可以简化成：

int DisjSet::find( int v ){
    return v==fa[v] ? x : (fa[v]=find(fa[v]))
}

这也是为什么并查集被很多OIer和ACMer认为是最简洁和优雅的数据结构。如果从我个人的审美来看，并查集和堆一样，是计算机简洁而强大的威力的体现，体现了算法设计之美。而其中并查集的简洁和美感又远超堆。

希望大家能体会这种美感。

秩和进一步优化

对于绝大多数场合，经过路径压缩的算法足以满足要求（例如我们的OJ）。不过算法还有优化的空间。

在加入路径压缩之后，有一种误解，就是经过路径压缩的图都会变成菊花图。实际上并非如此。

我们看一个非常极端的情况，比如上面的例子中，如果我们把连接的方式稍加修改：

E--F
D--E
C--D
B--C
A--B

你还是会得到一条线的结果。

所以我们可以思考一个问题，当两个集合合并时，究竟应该选择谁合并谁？

考虑下下面两种情况：

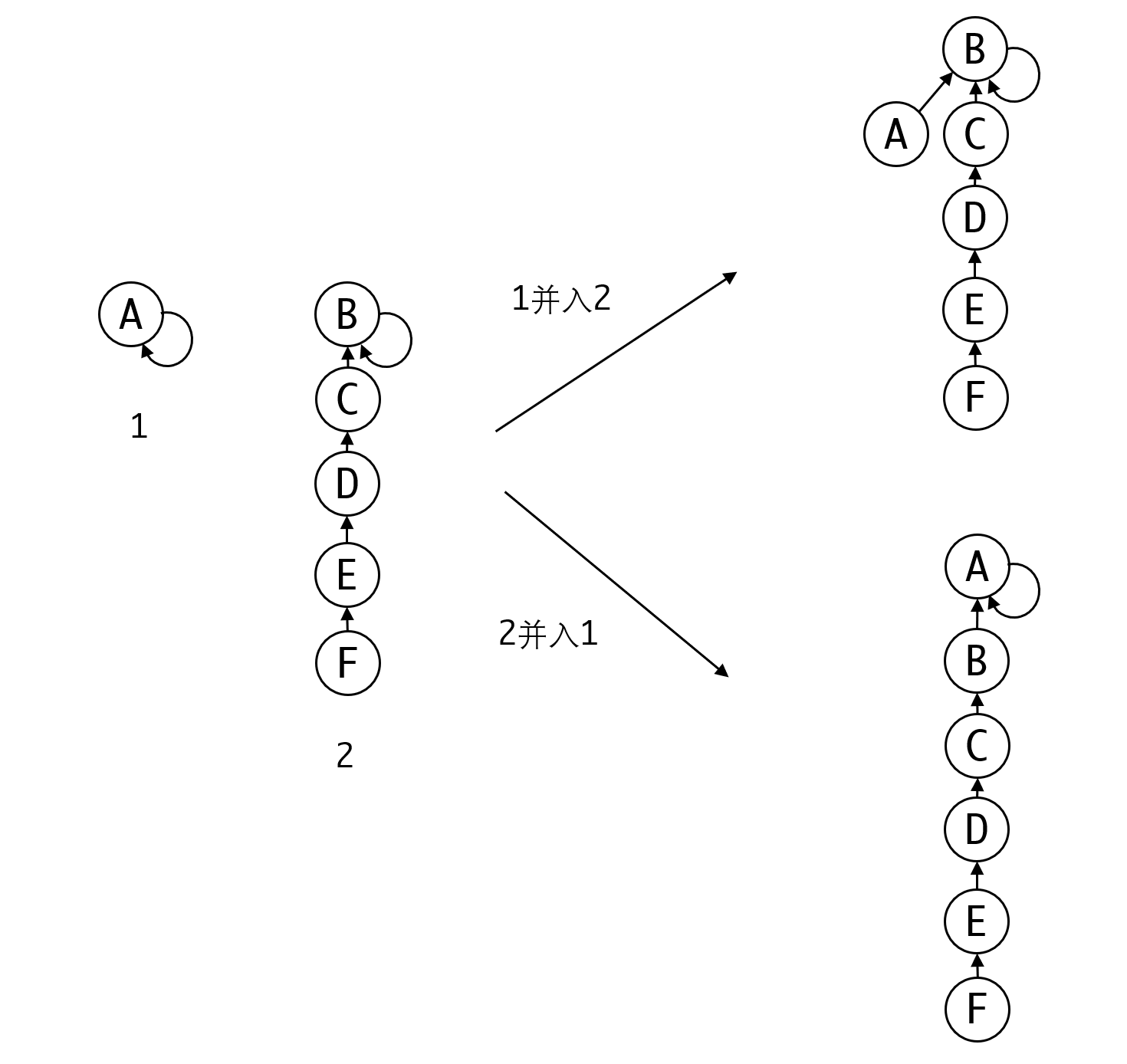
显然将2并入1的做法，恶化了整体的结构。而1并入2则至少维持了当前的结构，没有进一步恶化。

这提示我们要把树比较低的集合并入树比较高的集合。

但且不说树高好不好求，他至少也是一个$O(n)$的操作，这又违背了令并查集如此高效的原则——操作都是顺带进行的。

这里我们可以用空间换时间，把高度记录下来，我们称为秩。

struct DisjSet{
    vector<int> fa;
    vector<int> rank;  // 秩
    DisjSet( int size );
    int find( int v ); 
    void merge( int v1, int v2 );
};

DisjSet::DisjSet( int size ){
    fa.resize(size);
    for( int i=0; i<size; ++i){
        fa[i] = i;
        rank[i] = 1; // 初始秩为1
    }
}

void DisjSet::merge( int v1, int v2 ){
    v1 = find(v1), v2 = find(v2);
    if( rank[v1] <= rank[v2] ){
        fa[v1] = v2;
    }
    else{
        f[v2] = v1;
    }
    if( rank[v1] == rank[v2] && v1!=v2){ // 两者相等时
        rank[v2]++; // 此时v1被合并到v2，所以v2的秩要加1
    }
}

注意这里的细节，只有当两个合并的集合的秩相等时，我们才需要将合并得到的代表元素的秩加一，大家可以画一下图体会下这种情况。

而当两个秩不同的集合合并时，我们总是把秩小的集合加入大的集合，新集合的秩会等于原来比较大的那个集合的秩，所以我们不用处理。

需要注意的是，由于路径压缩的存在，秩并不一定（或者说大概率）不等于这个树的真实高度，而是等于树的高度上界。所以这不是一种严格意义上的最优解。