线性表算法与应用

两个线性表求并

要求

两个线性表A和B，各自内部都没有重复元素，求他们元素的并集，例如：

合并后得到：

解法

这一算法是比较容易想到的。解法也不止一种，以下是一种比较常见算法的描述：

1. 复制任意一个线性表到新线性表，不妨设复制A。
2. 对B的任意一个元素b，在新表中查找相同值的元素。
3. 如果2步中查找到相同值的元素，跳过b查找下一个。
4. 如果2步中没找到相同值得元素，插入（追加）一个值为b的元素。
5. 重复2~4的步骤，直到遍历完整个B。

通过这几个步骤，我们把这个要求转换成几个最基本的线性表操作：遍历，插入，追加，查找等等。 然后就可以用我们丰富的经验来击败他了，这里给出顺序表的解法：

SEQUENCE union_sequence( const SEQUENCE& a, const SEQUENCE& b ){
    SEQUENCE seq(a.count+b.count);               // 需要返回的顺序表，预留空间为A和B的总长度
    for( int i=0; i<a.count; ++i ){              // 复制顺序表A到需要返回的顺序表
        seq.append( a.data[i] );
    }
    for( int i=0; i<b.count; ++i ){             // 对B的所有元素
        if( seq.search(b.data[i]) != -1 )       // 如果在seq里已经存在则不应该插入
            continue;
        else                                    // 否则将其插入
            seq.append(b.data[i]);
    }
    return seq;
}

语句的注释上写的很清楚，就不解释了。

这里我们使用的函数都是之前介绍过的顺序表的函数。请记住将新问题转换为已经解决的问题很多时候非常有效。

const SEQUENCE& 是个什么东西？

你可能注意到这里的参数用的是const SEQUENCE&这种类型（对于C，这里应该是const SEQUENCE*）。 这是什么类型？我们又为什么要用他来传递参数？

这首先是个引用SEQUENCE&（对C，是个指针SEQUENCE*），前面的const限定符告诉编译器， 这个引用（指针）在函数的内部是不可变的。也就是说在union_sequence内部，这个引用只能看，不能修改。

这里对引用是比较好理解的，但对指针来说，请注意他表示指针指向的空间不能修改，而非不能给这个指针赋值新值：

//struct Node{
//    int   value;
//    Node* next;
//}

const Node* p = head;
p->next = tail; // 不行！不能改变p的内容
p = p->next;    // 可以，p的值，也就是他的指向可以改变

为什么采用这种传参方式？

首先你可以看出这是一种引用传递，不是值传递。我们使用引用传递最重要的目的在于让函数内部可以修改这个引用（即这里的seq）。 但本例显然不是这样的。另一个比较隐蔽的原因是引用传递的开销远小于值传递：

void f_ref( A& a);
void f_value( A a);

这样两个函数在调用时，f_ref只需要将参数的指针复制给a即可，开销是一个指针的开销。 而f_value需要将整个参数的值复制给a，开销是sizeof(A)。 因此在所有复杂类型传参中，我们都应该使用引用传递，而非值传递。

但这样带来一个隐患，对于函数f_ref的调用者来说，他会有顾虑，我把&a传递给你。 你偷偷给我改了怎么办？这就是const要解决的问题。

const限定符保证引用（指针）a（指向的空间）在f_ref的内部不会被修改， 否则会触发编译器错误。这样调用者就可以很放心地把变量以引用的方式传递而不用担心被改变了。

这一传参方式是非常常用的传参方式，甚至可以说是唯一限定的传参方式，一定要理解。

我们再来看看链表的写法，以带头节点的单链表为例：

Node* union_list( const Node* a, const Node* b ){
    Node* ret = new Node;
    ret->next = nullptr;
    Node* node = a->next;
    while( node ){      // 复制链表a的值，注意这里的次序跟原来的不同
        insert_head( ret, node->value );
        node = node->next;
    }

    node = b->next;
    while( node ){
        if( !search_node( ret, node->value ) ){  // 搜索不到node->value
            insert_head( ret, node->value );     // 就将其插入新链表
        }
        node = node->next;
    }

    return ret;
}

这里的函数insert_head用来在链表头部插入一个元素。 之所以在头部插入，因为要求并没有限定结果的次序，头插的速度要更快一些。

从逻辑上说，顺序表版和链表版并没有太大区别。

复杂度

我们先看这个算法的时间复杂度。

从前面算法的描述上我们可知， 算法的主要时间开销在于对b的每个元素，我们都要在新表中轮询一次，查询其是否存在。 而查询的时间复杂度是$O(n)$，最坏的情况是找不到，我们需要从头到尾遍历一次才能知道没找到。

考虑最坏的情况，b的每个元素在新表中都不存在，也即a和b的元素没有重叠。 那么b的每个元素都要完整遍历一次新表。所以我们有最坏的时间复杂度$=O(m\times n)$。

而算法执行时我们并不需要额外分配新空间（注意新表是要返回的，不能算在算法开销里）。所以算法的空间复杂度是$O(1)$。

拓展思考

1. 还有其他算法可以解决这个问题吗？复杂度是多少？
2. 这个算法还有进步的空间吗？
3. 如果要你求交（只留下共同元素），求异或（即$(A\cap \bar{B})\cup(\bar{A}\cap B)$，求不同时处于A和B的元素）。要如何处理？

有序线性表拼接

要求

两个有序线性表（数字可以重复），要求合并两者，并使结果也保持有序。

合并后得到：

解法

最简单的解法当然是两个线性表先简单连起来，然后再排序。 但排序算法的复杂度至少为$O(nlogn)$，且有较多的限制。 例如快排和堆排都要求要有随机访问能力，也即无法应用于链表。

仔细思考下，这两个表都是有序的，我们可以围绕这点来做文章：

1. 分别用两个指针（或者下标）指向两个线性表的头元素
2. 对比两个指针指向元素的大小，把较小的那个插入到新链表中，并将其向后移动
3. 重复上述过程，直到某个线性表被遍历完
4. 把剩下未遍历完的线性表复制到新链表的最后部分

如下图：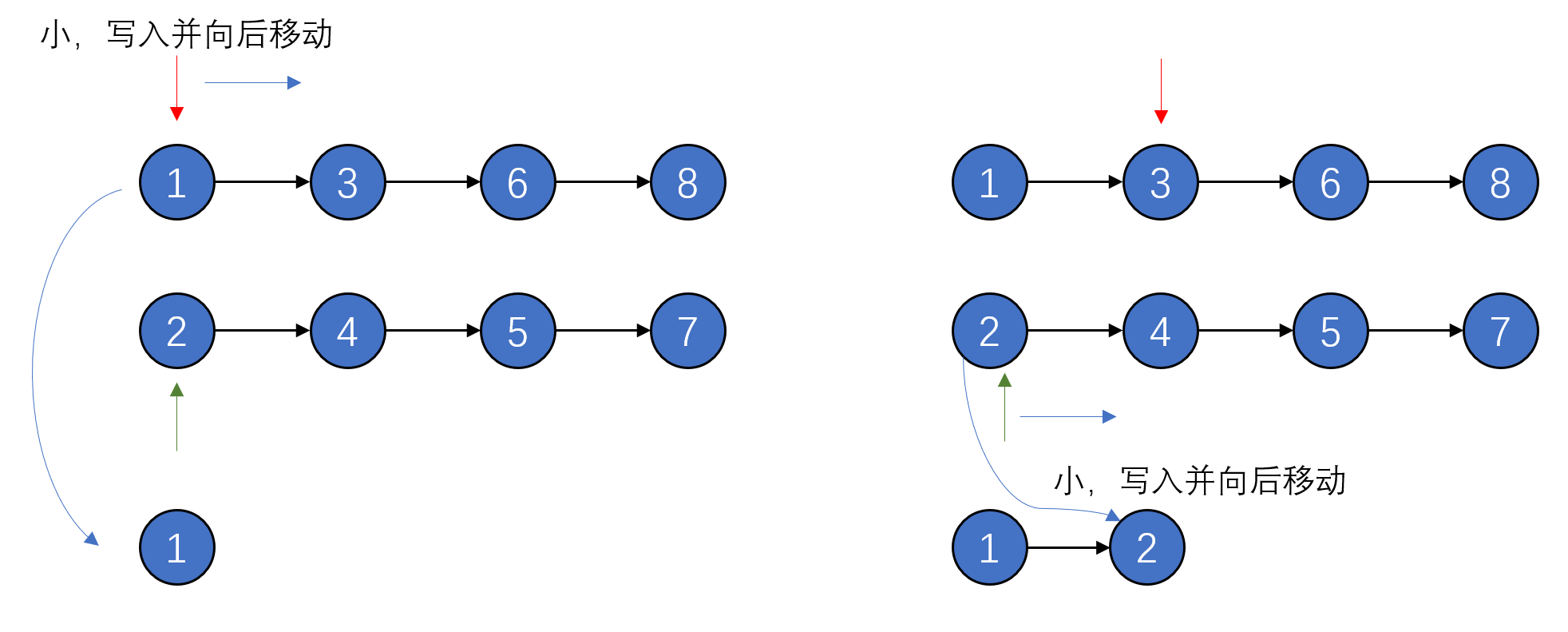

由于两个表都是有序的，在这一过程中，可以保证指针前的元素都已经被放入新表中，也即只有指针前面的元素需要处理，有效地降低了复杂度，我们用一个最极端的例子来看一下：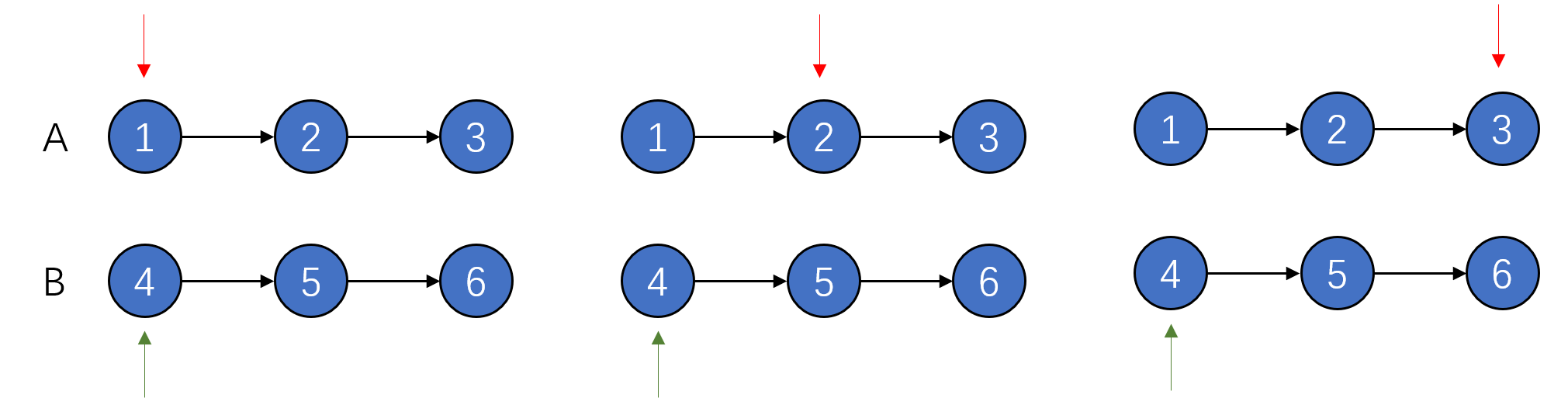

在这个例子里，A表的元素都比B表的元素小。 我们可以看到，在整个过程中，对应B的指针始终处于首个元素的位置原地踏步。

希望通过这个例子能让你更好的理解这一算法运作的过程。

这个算法这里不再给出代码了，请自行尝试。只要小心指针的移动，就不难写出来。

另一点需要注意的是，当把算法应用于链表时，要如何降低新链表插入元素的复杂度。

复杂度

显然我们也没有使用额外的空间，因此空间复杂度为$O(1)$。

时间复杂度上，很显然两个指针都只向前移动，从没有回溯过。因此指针总移动的次数是$m+n$次，所以时间复杂度为$O(m+n)$

拓展思考

这个算法的复杂度很明显低于前一个算法。这显然得益于有序这一条件。

实际上在有序的序列上执行某些操作，我们总有办法把他的复杂度降下来。因为有序有一个非常好的性质。即在某一点上，前面的元素总是小于后面的元素。

通过这点，我们要么可以排除他前面的元素，要么可以排除他后面的元素，这就可以有效地降低复杂度。

那么思考一下：

1. 如果上节的要求里的线性表也是有序的，有可能进行加速吗？
2. 如果两个线性表都是有序的，求交或者求异或，可以加速吗？

双指针

要求

删除顺序表中指定值的所有元素，并要求时间复杂度尽可能的低。 例如下面的顺序表中，要求删除所有的2。

解法

我们先考虑最简单的解法，秉承把问题转化为已有问题的原则。我们可以这样解：

1. 遍历顺序表的每个元素
2. 如果如果元素的值与所需要删除的值相同，则删除该元素

这个解法当然没有任何问题，绝对可以解决问题。只不过有一点点慢。 我们知道顺序表删除某个元素的复杂度是$O(n)$，而在这个算法中我们可能对每个的元素执行这个操作，因此时间复杂度是$O(n^2)$的。

在OJ上用这个方式刷这道题时，最后两个用例会TLE。

那么要如何加速呢？对于顺序表来说，通常一步移动到位可以比较好地优化算法。上例中，以最后一个5，即下标是7的元素为例。按上面的算法，我们在删除每个2时，都要向前移动一步。如果我们能够从7一步移动到4的位置，那么复杂度将大大降低。

于是对这种问题，我们有一种相对统一的解法，即双指针（或快慢指针）：用一个快指针向前指向目前要处理的元素，用慢指针指向当前要写入的位置。移动的策略上，慢指针当快指针遇到需要删除的元素时不向前移动（相当于删除了这个元素），其余时候两个指针同步移动：

1. 两个指针都指向头部
2. 如果快指针指向的元素是需要删除的元素，则快指针向前移动，慢指针不动
3. 如果快指针指向的元素不是需要删除的元素，则用快指针指向的空间覆盖慢指针指向空间，两个指针都向前移动
4. 当快指针移动到最后一个下标+1的位置时结束，此时慢指针指向的下标+1就是所剩余的元素数目

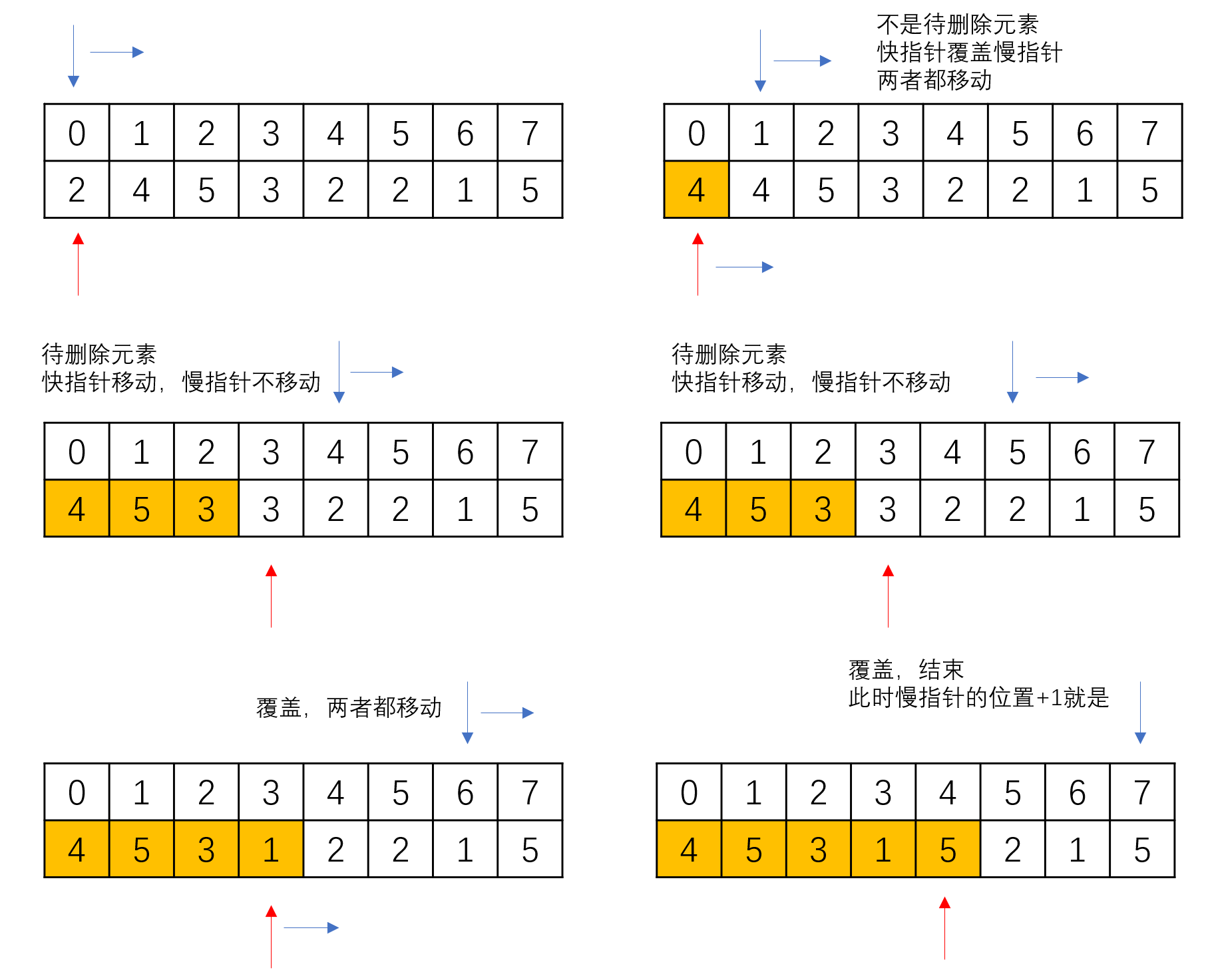
复杂度

显然整个过程中，快慢指针最多可能移动n次。所以整体的复杂度是$O(n)$。

拓展思考

快慢指针这种解法，应用范围非常广泛。某种程度上，删除单链表中指定值的元素也是快慢指针法的应用。你还可以思考下下面这些场景要怎么用：

1. 求单链表的中间节点
2. 删除有序顺序表（或链表）中的重复元素
3. 寻找最长不重复子序列

你还可以在力扣上找到很多双指针的问题。

一元多项式相加和相乘

一元多项式的表示

对于形如以下形式的多项式：

$P_n(x)=p_0+p_1x+p_2x^2+p_3x^3+...+p_nx^n$

要在计算机中保存，我们可以用一个n个元素的一维数组p来表示。即： 然后令其中的p[i]$=p_i$，多项式的次数则无需记录，因为下标i就隐式地记录了次数i。

例如给定p：

int p[4] = {3,0,2,1};

对应的多项式就是：$3+2x^2+x^3$

给定参数x，我们可以很容易用以下的代码来求得多项式的值：

int calc_polynomial( int* p, int num, int x ){
    int ret = 0;
    int x_pow=1;
    for( int i=0; i<num; ++i ){
        ret += p[i]*x_pow;
        x_pow*=x;
    }
    return ret;
}

多项式相加也非常方便，我们只需要将p1和p2对应的项加起来即可：

void add_polynomial( int*p1, int* p2, int* ret, int num ){
    for( int i=0; i<num; ++i ){
        ret[i] = p1[i]+p2[i];
    }
}

非常简单直观。 但这种表示方式的缺点也是非常明显的，对于系数稀疏（即有很多0系数）的一元多项式：

$1+x^{1000}+x^{2000}$

你需要用2001个元素的数组来放他，而这些元素大多数都是0，非常浪费空间。

那么就有下面这种用线性表表示的方式（以链表为例）：

struct PolyNode{
    int coef;
    int pow;
    PolyNode* next;
};

我们给每一项记录一个系数coef和一个幂次pow，这样上面的式子我们可以用3个元素的链表来表示：

多项式相加

在这种表示方式之下，我们考虑两个多项式相加：

$$P_1=3+2x-3x^2+2x^5\\ P_2=1+3x+3x^2+3x^3$$

转换为链表则是下面的形式，这里省略对应的参数名，前一个为系数，后一个为幂次，例如3,2，表示$3x^2$

我们要做的是求两个链表的并集，并对其中pow相同的项进行合并：

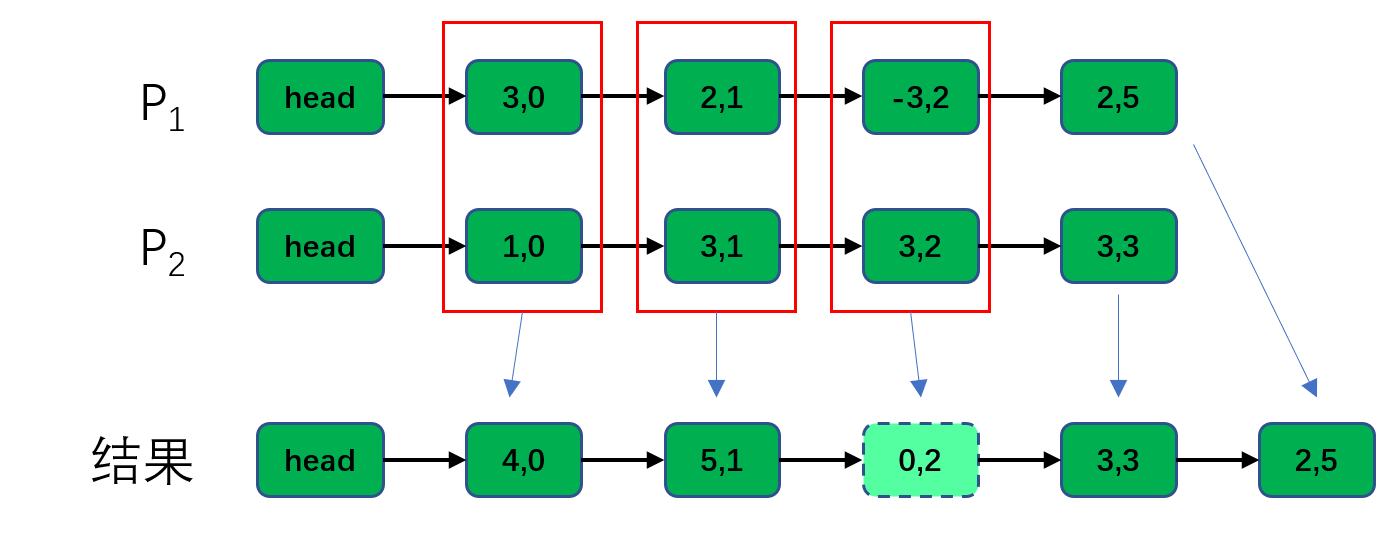
注意还要对参数为0的项进行清除，本例中我们只需要不将其复制到新链表即可。

聪明的你应该已经发现了，这里和有序链表的合并非常相似——链表的元素以pow有序排列，我们可以借鉴合并算法的思路，不难得到一个$O(m+n)$的算法：

1. 用两个指针分别指向P1和P2的首个元素
2. 对比两个元素pow项的大小，如果不相等，则复制小的那个元素到新链表，并将其指针向后移动一步
3. 如果两个元素的pow项相等，则合并将两个项的coef相加，得到新项的coef，两个指针同时向后移动一步
4. 如果3中的coef不为0，则复制新项到新链表中，否则则跳过一次
5. 重复2~4过程直到某个指针为空（即到了尾部）
6. 复制另一个非空指针剩余的项到新链表
7. 新链表即为多项式之和

拓展思考

1. +=操作要如何实现？即不分配新的链表，只在P1上完成添加的操作。
2. 要如何实现相乘？注意乘法用上面的+=可以一定程度上避免过多的内存申请和释放。

多项式乘法如何实现

多项式相乘可以分解为多个多项式的相加。 以上例的两个多项式为例：

$$P_1\times P_2 = P_1\times 1+ P_1\times 3x+P_1\times 3x^2+ P_1\times 3x^3\\ P_1\times 3x = 3x+9x^2+9x^3+9x^4\\ ....$$

算法请大家自行编写。