图的算法

XMUT.SE.DS2022年11月7日大约 11 分钟

图的算法

图算法是我们应用图的主要目的，在这里你可以看到很多的算法。

图的遍历

我们先从图的遍历开始。

我们在栈和队列那章已经见过在二维平面上进行的遍历了。实际上二维平面上的格子也可以看作一种特殊的图——格子看作顶点，如果两个格子之间相邻，就相当于顶点间有边相邻。从其中我们已经可以看出图遍历的基本形式了。

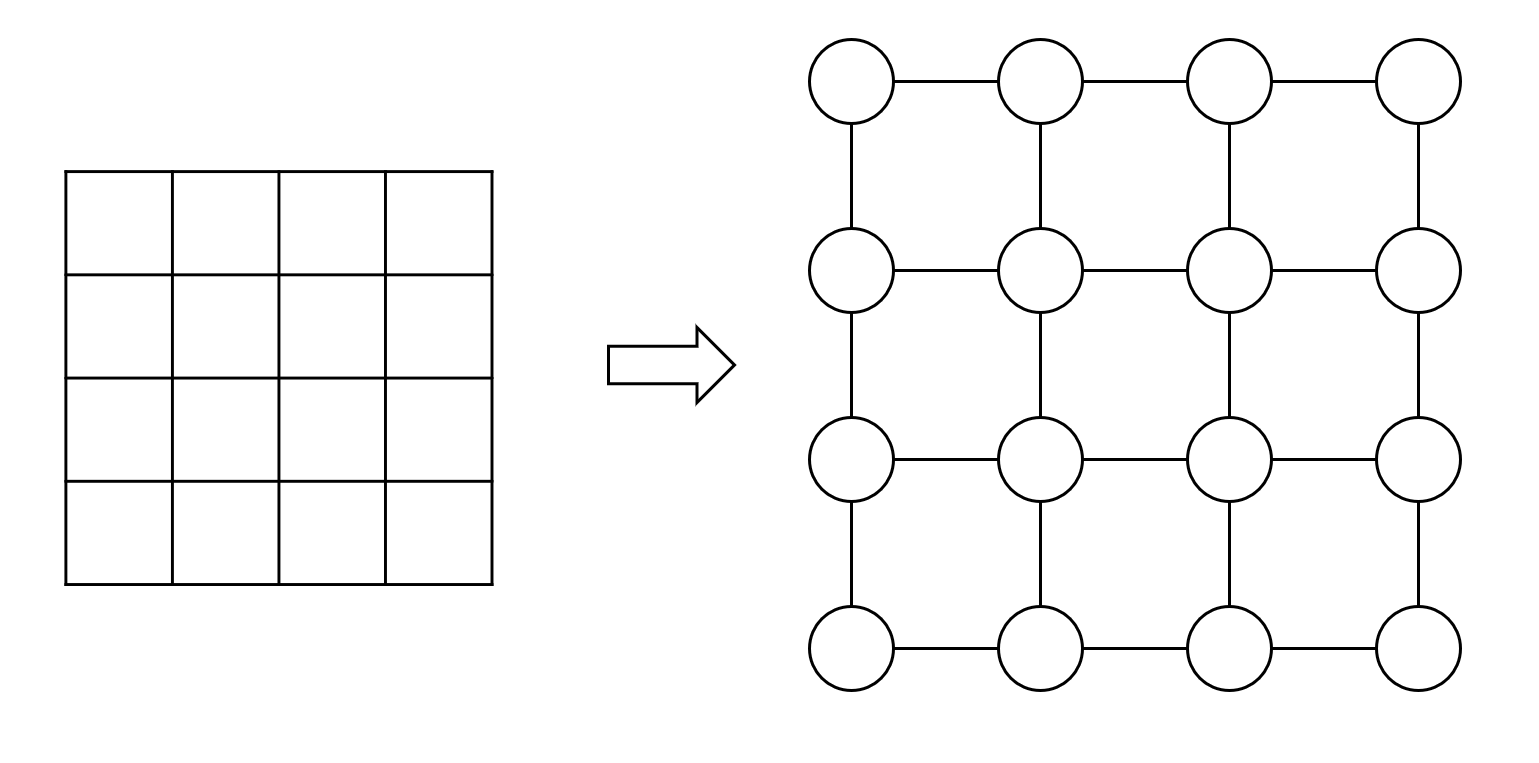
并且我们也得出结论——深度优先用栈（或者递归），广度优先用队列。这点在我们图的遍历里也是一样的。

如果我们把树的遍历和图的遍历做一个对比的话，会发现两者之间最大的区别是树的节点之间有比较严格的关系。因此我们在遍历树时，只要小心地选择遍历的算法再利用一些遍历的性质，就不会回到同一个节点重复遍历了。

真的不需要标记吗？

如果回忆一下中序和后序的非递归遍历，你应该会发现有时候标记也是需要的——我们需要知道某个节点是第几次访问。但正如我们前面所说，如果我们小心地选择遍历的算法（中序），或者很好地利用遍历的性质（后序），我们是不需要对树的节点打标记的。

其次在递归遍历中，我们完全不需要对节点进行标记，因为次序是确定的。我们不会两次踏入同一个节点。

而图的遍历则不同，顶点和顶点之间的关系非常的松散，我们有多种可能回到已访问的顶点。因此在图的遍历中，对顶点进行标记是必须的。这点第3章对二维平面的格子进行遍历的过程中也有所体现。

深度优先遍历

和树的遍历相似的是，深度优先遍历最简便的方式也是用递归来实现，这里我们给出伪代码：

void dfs( Vertex n ){
    set_visited(n);              // n设置成已访问
    cout << n << " ";            // 处理n
    for( Vertex v : adjacency(n)){  // 对n的每个邻接节点
        if( visited(v) )         // 如果已访问，则不处理
            continue;
        dfs(v);                  // 否则就要递归遍历
    }
}

代码非常清晰。

非递归遍历则会麻烦一些。

void travel_graph( Vertex n ){
    stack<Vertex> s;
    s.push(n);             // 根入栈
    while(!s.empty()){
        n = s.top();       // 取节点
        s.pop();
        if( visited(n) )   // 已访问则跳过，注意这句不能省
            continue;
        set_visited(n);    // 设置成已访问
        cout << n << " ";  // 处理
        for( Vertex v : adjacency(n)){ // 对每个邻接节点
            if( visited(v) )   // 已访问的不处理
                continue;
            q.push(v);      // 否则入栈
        }
    }
}

如果你认真研究这个过程，你会发现这个实现的方式存在重复入栈的情况，因为我们，在入栈时没有打标记，如果某个顶点已在栈中，而我们又第二次遇到该顶点时，他就会被重复入栈。但这是我们为了得到正确结果的处理，我们看图：

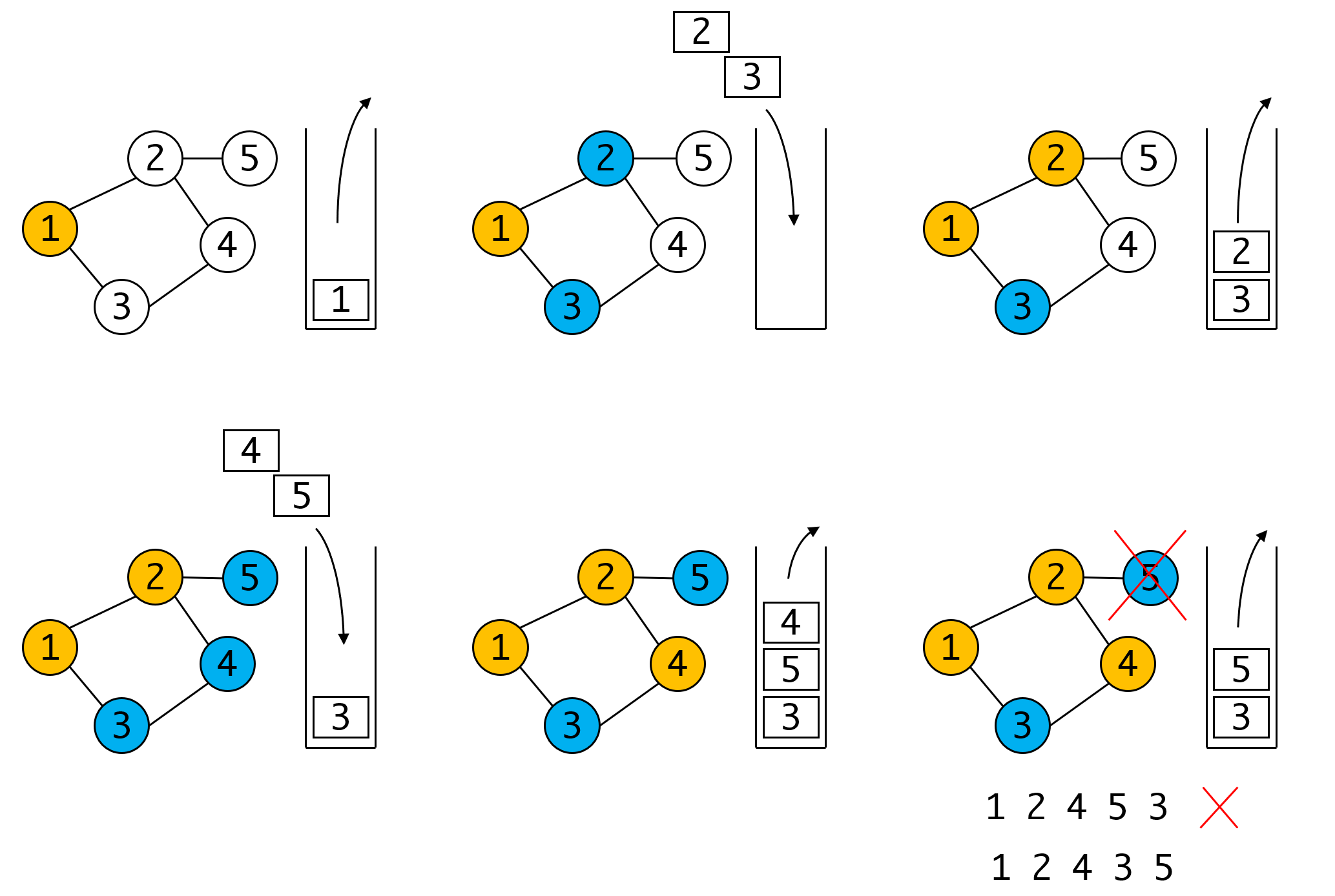
假如我们要避免顶点重复入栈问题，就需要在入栈之前为其打标记，已有标记的顶点不再入栈。在第二步时，我们将与1相邻的2、3都入栈并打上标记。但当我们遍历完4之后，由于与之相邻的3和5均已标记，所以此时没有任何顶点可以入栈，只能将栈顶顶点5出栈。这与正确的DFS遍历是不同的，正确的DFS应当继续从4往下遍历，直到这条线的顶点都遍历完毕，才会遍历5。

因此这里重复入栈问题是很难避免的，也正因为如此。我们在出栈时也需要再进行标记的判定（第7行）。我们看正确的流程：

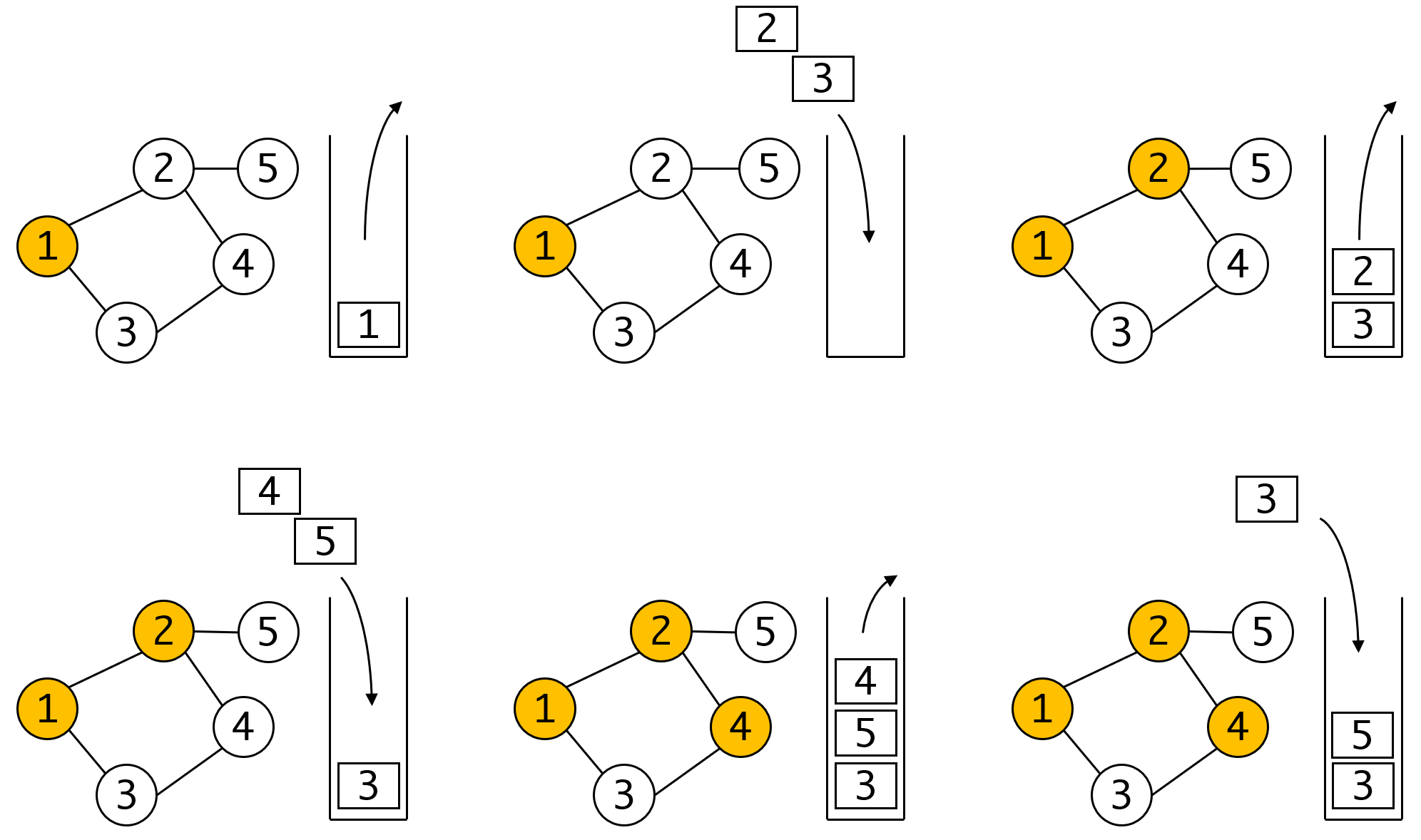
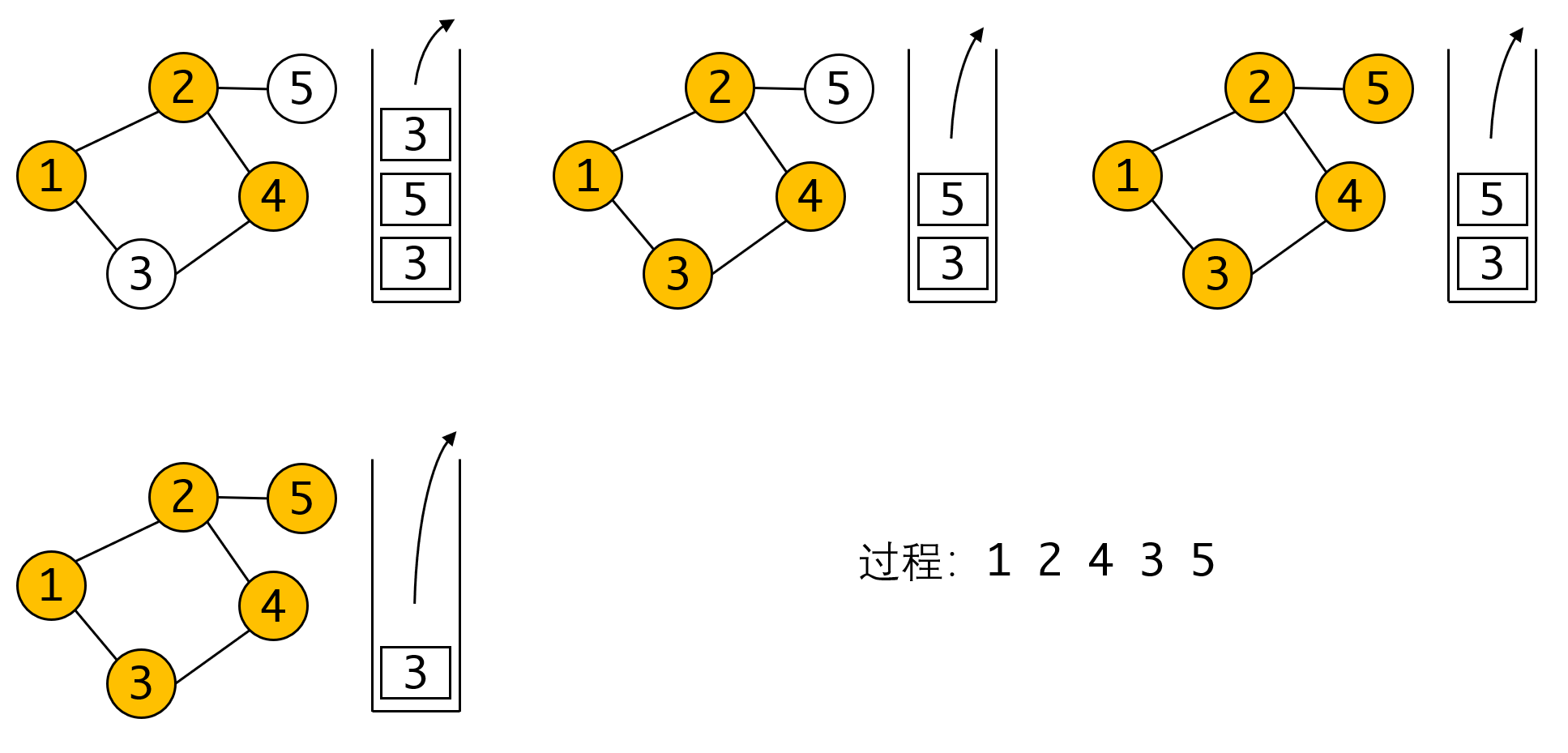
可以看出当我们遍历到4时，3被第二次入栈，但我们保证了整个过程的有效性。而当最后3再次出栈时，因为其已被标记，会被过滤掉，也就不存在重复遍历的问题了。

为什么要递归

因为简洁且方便

从图和树的例子我们都可以看到递归的强大威力。虽然我们可以用栈来实现相同的要求，但总需要一些技巧，或者关注一些特殊的情况，才能得到正确的结果。

在大多数场合下，递归的代码总是更简洁，更清晰，也更容易理解的。

广度优先遍历

相比深度优先遍历，广度优先遍历则没有什么特殊的情况需要处理，直接用队列处理即可。跟深度优点遍历一样，我们也需要为已访问的节点打标记。由于队列的顺序性，我们直接在入队的时候标记即可。

void bfs( Vertex n ){
    queue<Vertex> q;
    q.push(n);
    set_visited(n);
    while(!q.empty()){
        n = q.front();
        q.pop();
        cout << n << " ";
        for( Vertex v : adjacency(n) ){
            if( visited(v) )
                continue;
            set_visited(n);
            q.push(v);
        }
    }
}

我们再看一个具体的例子：

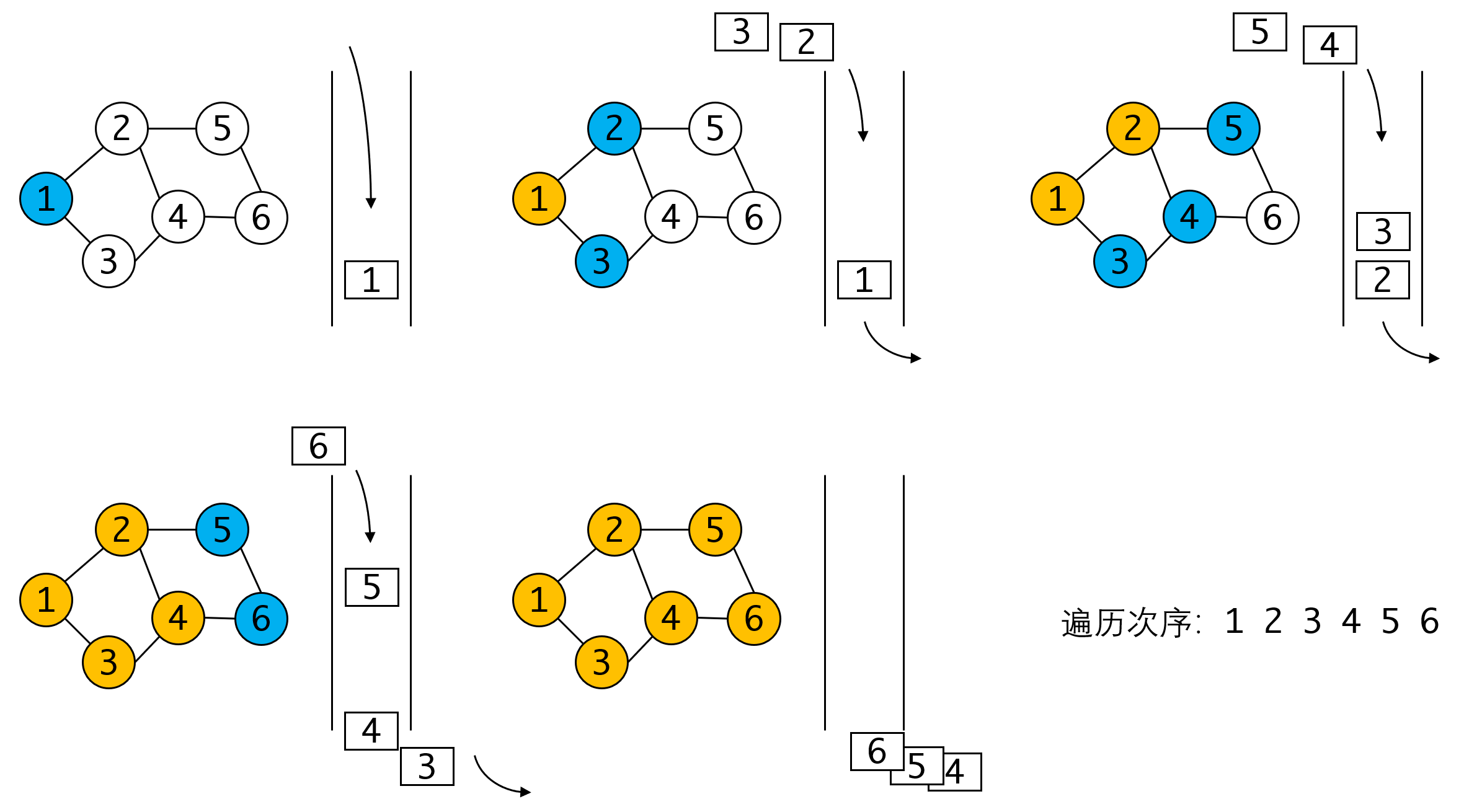
很简洁不解释。

我们可以发现遍历的次序是按遍历开始点的亲疏远近一圈圈向外扩散的。

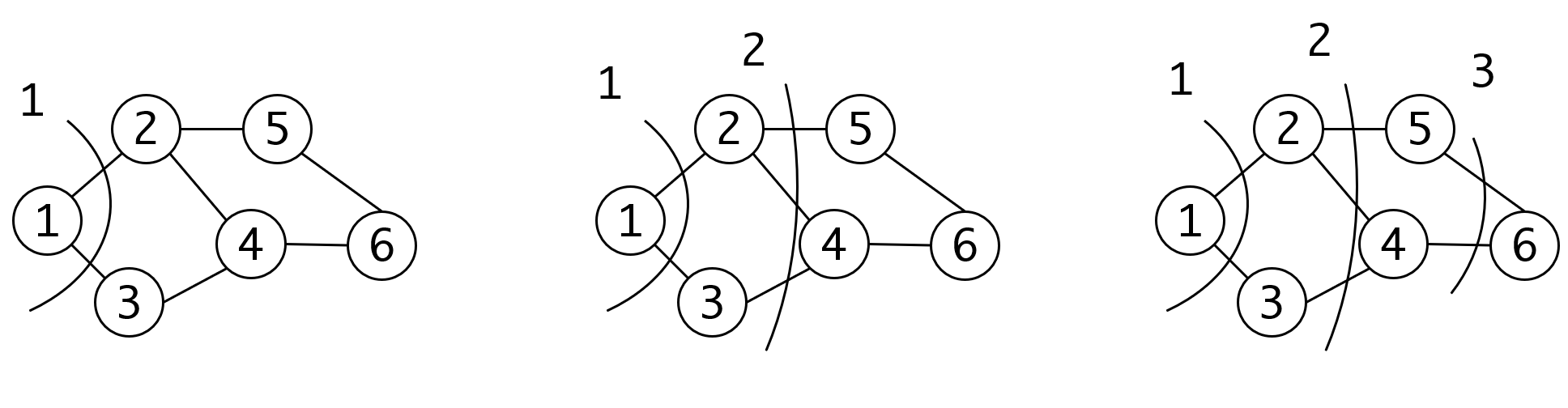
这和我们在二维网格上的遍历结果是一致的。

最小生成树

生成树是连通图的包含所有顶点的最小连通子集，用人话说就是：用最少的边连接所有的顶点。

显然对于 $n$ 个顶点的图来说，他的生成树会有 $n-1$ 条边，这也是连通图边数目的下限。

显然对于一个图来说生成树并不唯一：

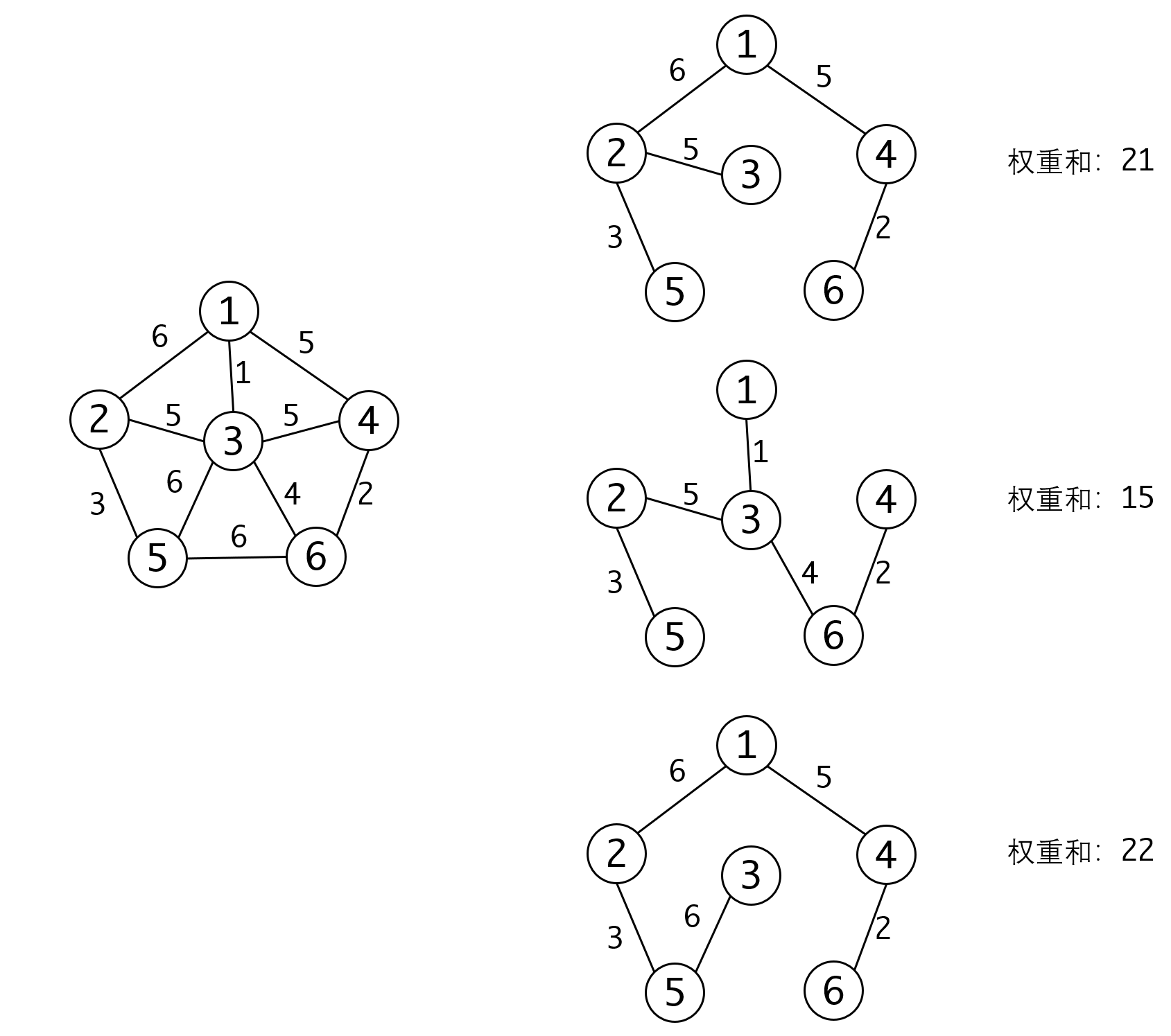
对于带权图，我们自然地会想，能不能获得权重和最小的生成树，我们称这种生成树为最小生成树。上图中，中间权重和为15的生成树就是最小生成树。

研究最小生成树非常有实际意义。因为生成树是边数最少的可以连通所有顶点的图，而最小生成树拥有最小的权重和，那么就意味着我们可以用最小的代价（权重）连通所有的顶点。

设想一下，你是电信的线路规划师，要求你用最小的代价连接一片小区。又或者你是规划道路的设计师，要求你用最小的代价连通几个村庄。这些都是最小生成树可以发挥作用的场景。

因此我们非常需要可以帮我们生成最小生成树的算法。这样的算法有两种比较典型，分别是以选择顶点为核心的普利姆（Prim）算法，和以选择边为核心的克鲁斯卡尔（Kruskal）算法。

Prim算法

从一个顶点起步，每次选入一个顶点，直到所有顶点都被选入，这就是Prim算法的基本思想。

我们可以这样描述整个算法：

1. 集合S表示选入的顶点，集合C表示待选顶点。
2. 任意选择一个顶点开始，将其放入集合S中。
3. 在C中选一个与S中顶点相邻并且相邻边最小的顶点V，加入集合S中
4. 重复2、3直到所有顶点都被选入。

我们看下执行的过程：

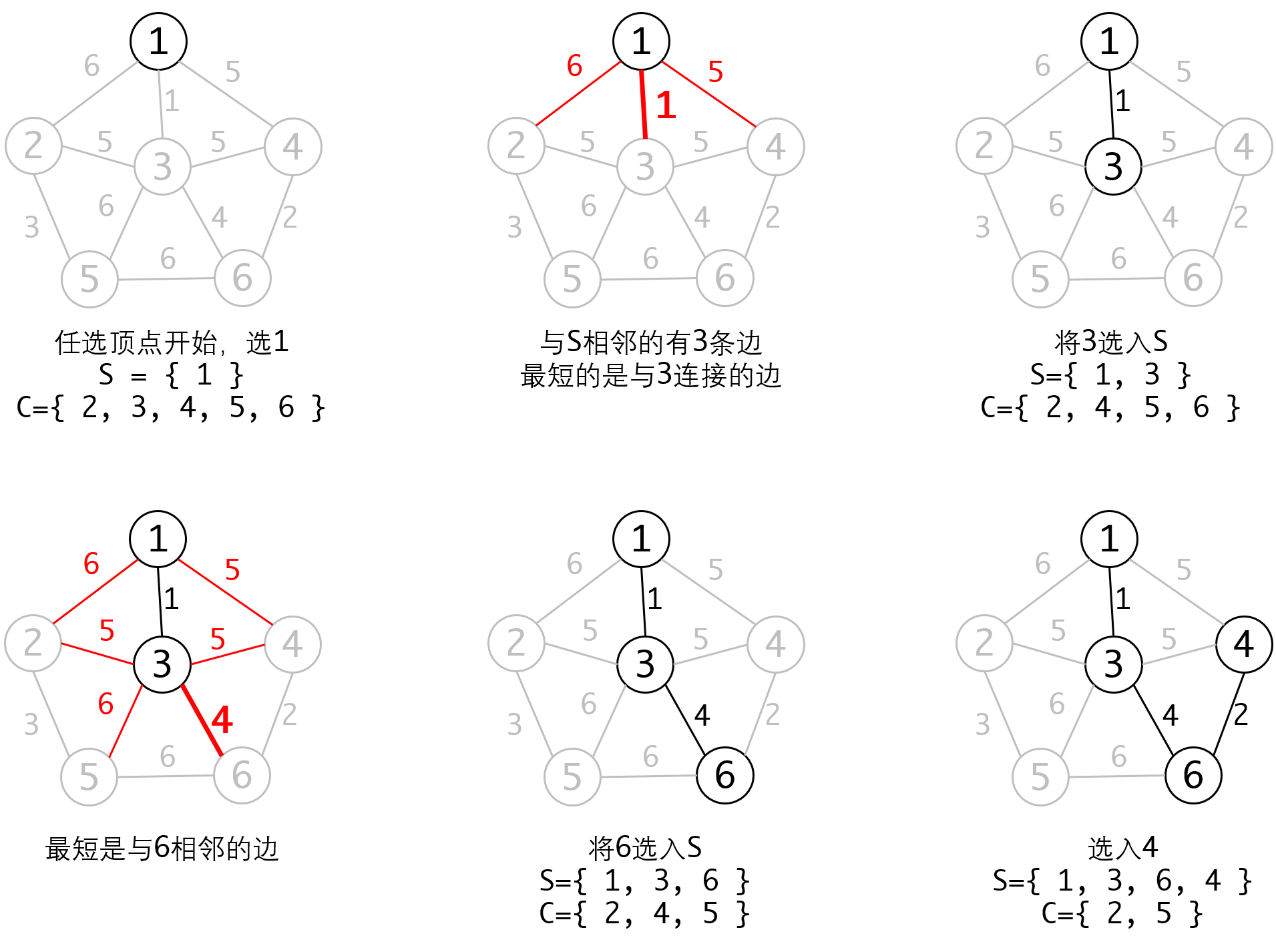
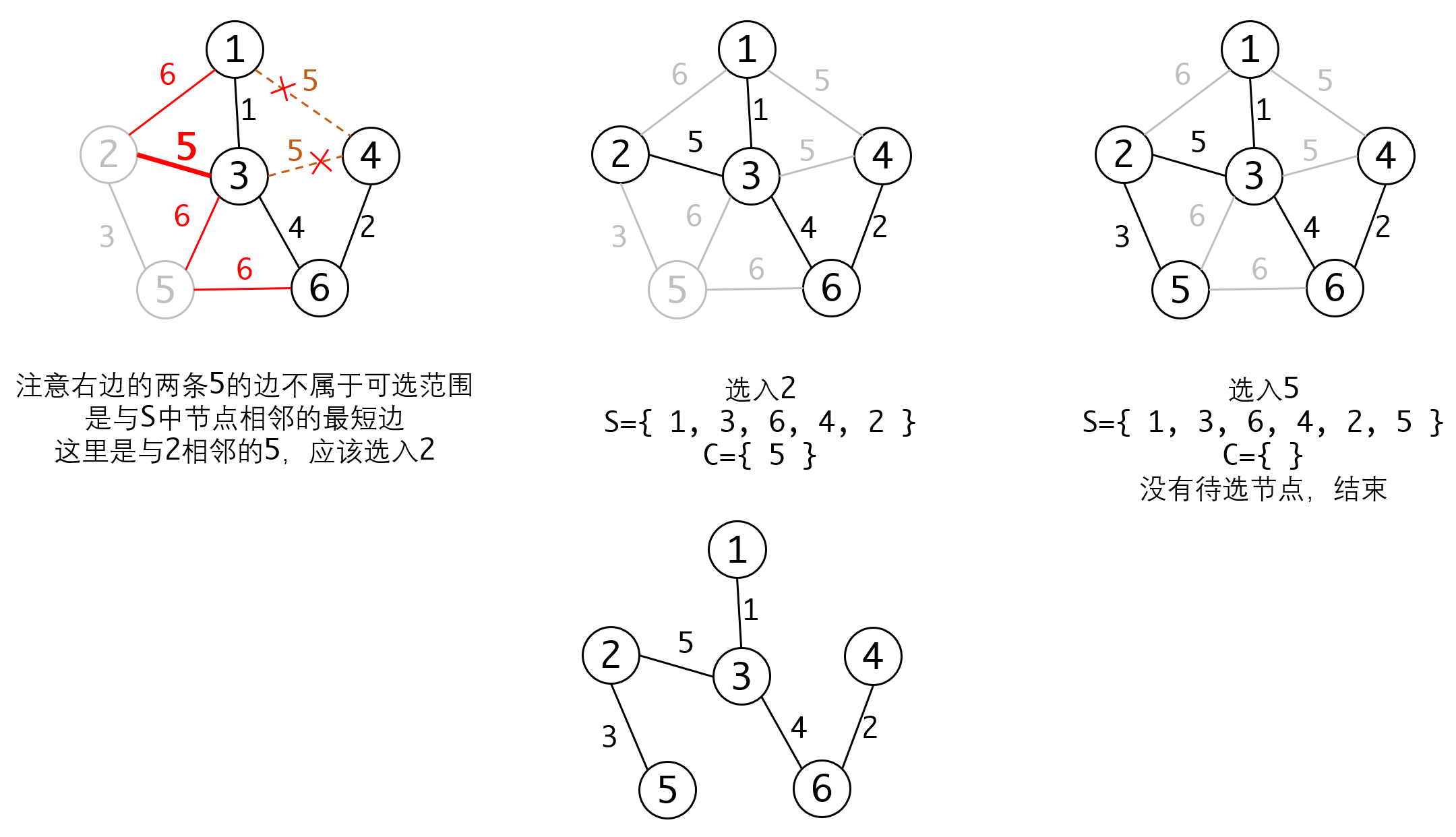
Prim算法的特点是：

以顶点为单位执行，一次选入一个顶点
每次选择都选择与已选入顶点相邻的边中最小的那条

具体实现的过程中，如果我们每回合都遍历S和C，选择其中最小的边来加入，这个过程的时间复杂度是 $O(n^2)$ ，整体的时间复杂度就是 $O(n^3)$ ，显然太高了。

我们可以维护一个数组，保存C中每个顶点与S中顶点的邻接边的距离。当我们从C中选入一个顶点V时，我们只需要更新与V相邻的所有顶点的距离即可。这样可以把更新的复杂度降低到 $O(n)$ ，从而使整体复杂度降低到 $O(n^2)$ ：

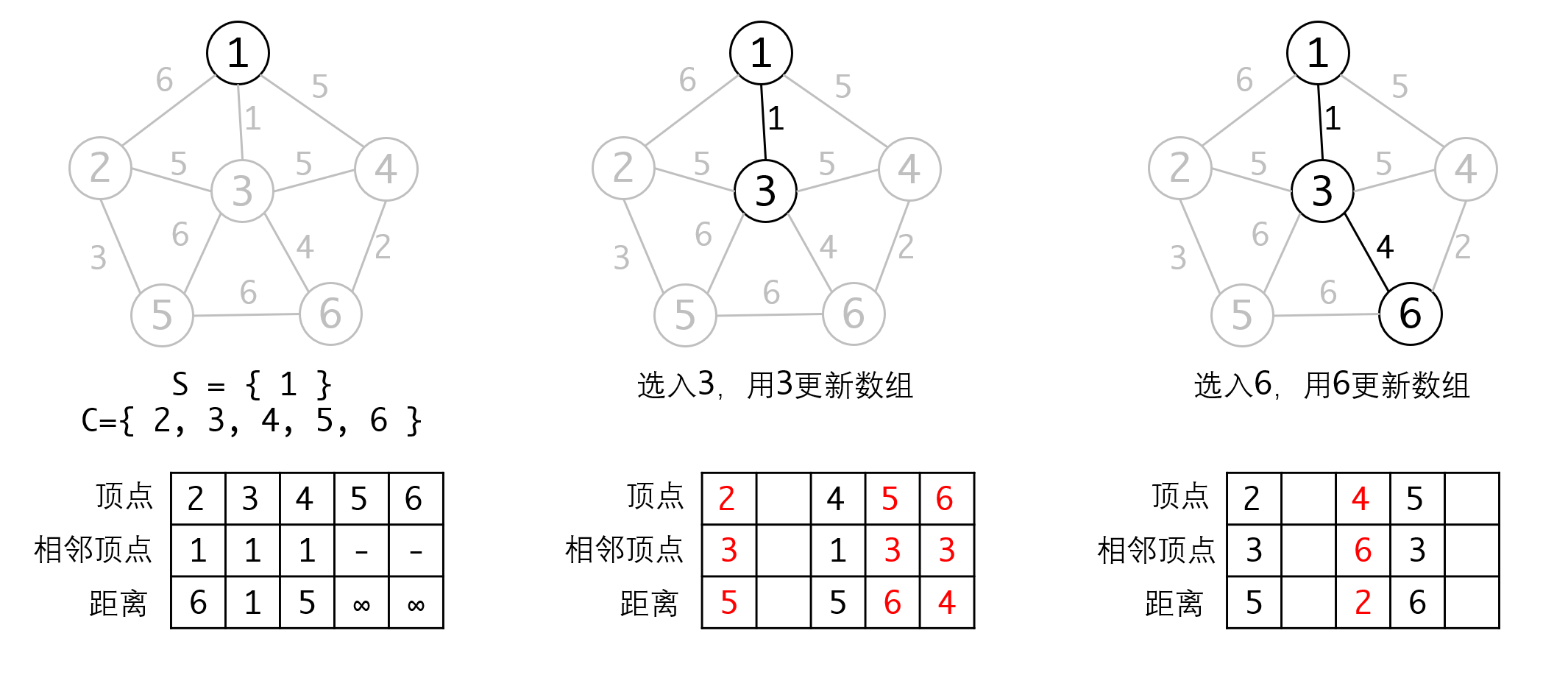
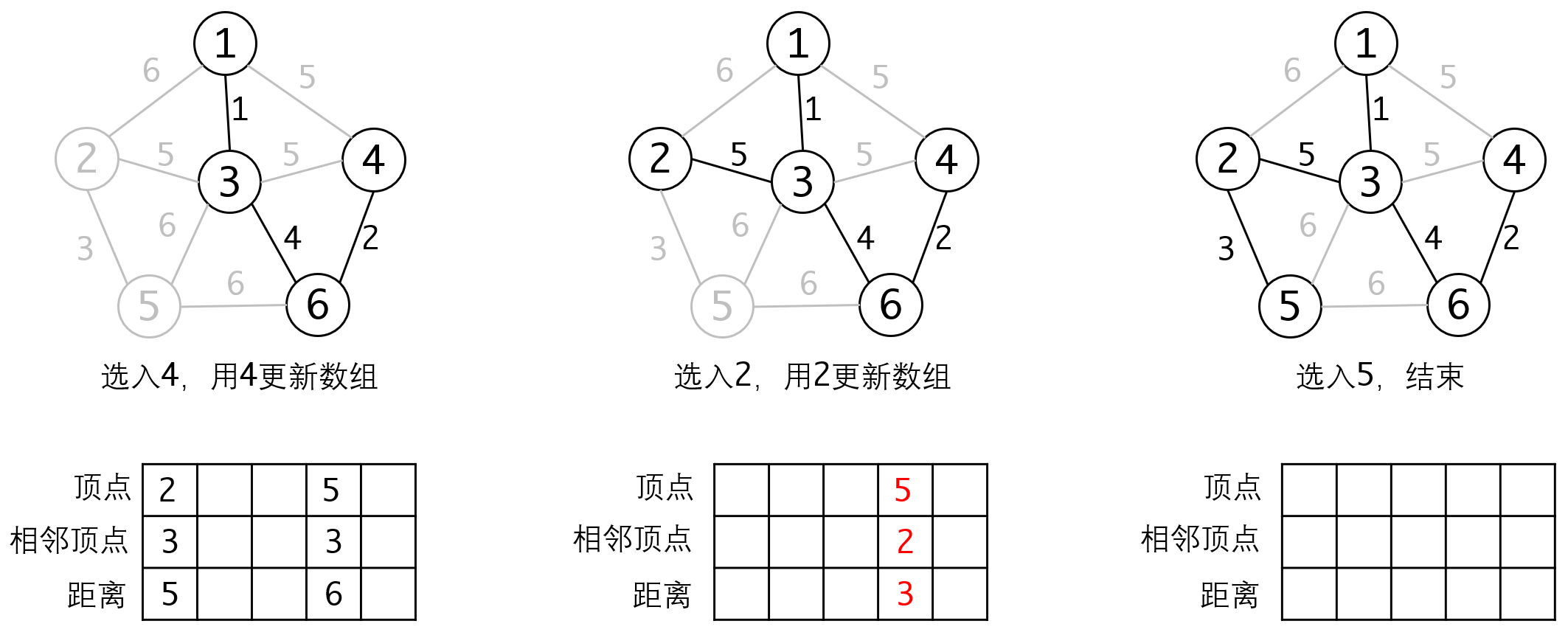
这个过程跟我们后面要讲的Dijkstra算法非常相似。

Kruskal算法

Kruskal算法则从边入手来解决问题，从逻辑上看，他比Prim算法要简单：

1. 选所有边中最小的一条边
2. 在剩下的边中选择一条新边，但必须保证选入结果不成环
3. 重复2直到选入n-1条边

同样的我们看下执行过程：

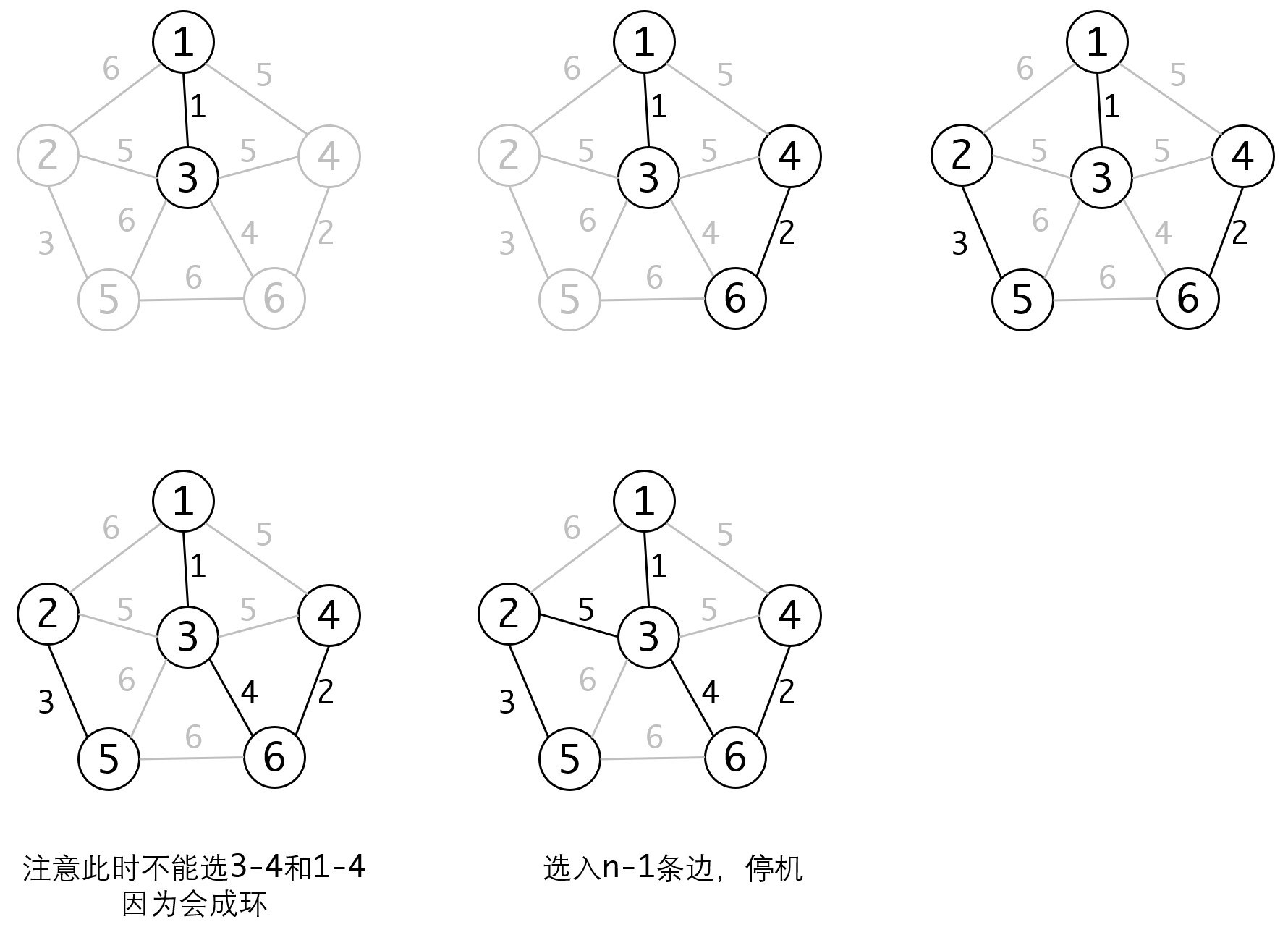
Kruskal算法不需要每回合都更新距离，算法逻辑上比Prim算法要简洁，但他有一个比较麻烦的问题，即如何判断选入某条边之后会成环。像上面的倒数第二步，此时2-3、3-4和1-4这三条边的长度都为5，好像任选一条都可以。然而实际上1-3和1-4都会导致已选入的子图成环，因此只有2-3是可选的。

那么要如何判断是否会成环呢？这实际上也是连通性的判断：当选入边的顶点处于同一个连通分量中时，再选入这条边就会成环。也就是说，待选入的边必须属于不同的连通分量，这点画一下图就非常清楚：

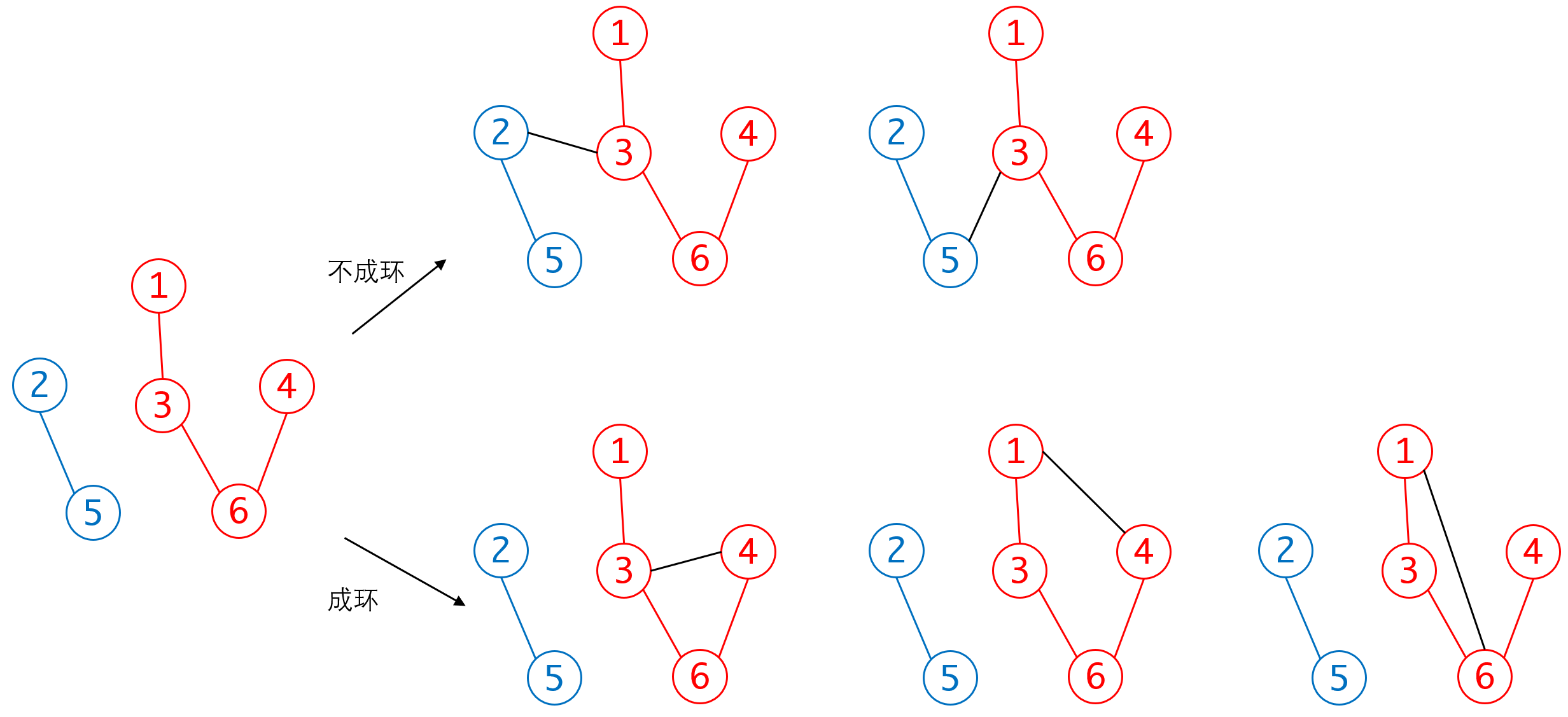
在同一个连通子集内部建立新边，就会成环，反之在连通子集之间建立新边，就不会成环，非常清楚。

于是成环判断就转为：如何判定两个顶点不在同一个连通子集内部。这点比较有效率的方法可以通过上一章的并查集来完成。如果对效率要求不高的话也可以直接用BFS或者DFS来判断。

Kruskal算法每一回合都要选择其中最短的那条边，这个操作的复杂度是 $O(e)$ （ $e$ 是边的数目），整个过程要执行 $n-1$ 轮。所以他的复杂度是 $O(e^2)$

算法分析

Prim算法和Kruskal算法的特点非常鲜明，一个以顶点为基础进行选择，一个以边为基础进行选择，他们的复杂度都是 $O(n^2)$ 这个级别的。只不过一个的n是顶点数目，另一个是边的数目。

他们也都有额外的开销，对于Prim算法来说，他需要维护一个最短边的数组并在每次选入新顶点之后进行更新，也就是说他有 $O(n)$ 的空间复杂度。对于Kruskal算法来说，他需要进行成环的判断，也会增加处理的复杂度和额外的开销。

显然Prim算法适合顶点少而边多的稠密图，而Kruskal算法正好相反，适合顶点多而边少的稀疏图。

此外，和哈夫曼树相似的，最小生成树并不是唯一的。无论Kruskal算法还是Prim算法，都可能遇到有两个备选项的情况，此时选任何一个都可以。虽然最终得到的树可能不是同一棵，但他们都拥有相同的带权和。

优化

如果我们仔细分析两种算法的执行过程的话，我们会发现他们有一个共同点：每一回合都选择最小的某条边。而每一回合的复杂度也主要消耗在这一过程中。回顾一下上一章的相关内容，对于选择最大或者最小元素的操作，我们可以通过堆来进行优化，从而使其复杂度变为 $O(logn)$ ，这样整体的复杂度就可以降低到 $O(nlogn)$ 。

对于Kruskal算法来说，这一过程是非常容易的，我们只需要在一开始将所有的边都放入堆中构造堆，就可以在之后的算法中取出来使用。构造堆的复杂度是 $O(nlogn)$ ，算法执行的复杂度也是 $O(nlogn)$ ，所以总复杂度就是 $O(nlogn)$ 。

但对于Prim算法来说，就比较麻烦，因为他每一回合需要更新最短边的值。比如上面的例子里，节点5的最短边从最初的无穷大，更新为6，再更新为3。对于已经放入堆的元素，我们是不可能对他进行更新的。那么要如何处理呢？

很简单，不用处理就可以了。我们完全可以将新结果直接放入堆中。从堆里取出元素时，再进行重复性判断。也就是说在最后，堆里可能有三个顶点5的元素。因为堆总保证每次可以取出的是最小的元素，所以更新后的结果总会先于旧结果出堆，也就不会对算法造成问题了。

图的算法

# 图的算法

# 图的遍历

# 深度优先遍历

# 广度优先遍历

# 最小生成树

# Prim算法

# Kruskal算法

# 算法分析

# 优化

图的算法

图的遍历

深度优先遍历

广度优先遍历

最小生成树

Prim算法

Kruskal算法

算法分析

优化