二叉搜索树（排序树）

XMUT.SE.DS2022年12月3日大约 5 分钟

二叉搜索树（Binary Search Tree, BST）顾名思义就是为了方便进行数据搜索而设计的树。和其他树相似的是，我们可以通过递归定义来定义搜索树：

定义：搜索树是这样一棵树，他左子树（如果有）的所有节点都比根节点小，右子树（如果有）的所有节点都比根节点大，同时子树都满足这一条件。

这里要强调一下，搜索树的定义是一个递归定义。不仅仅是左（右）节点要比根节点小（大），而是子树上的所有节点都要比根节点小（大）。

如下图就是一棵搜索树：

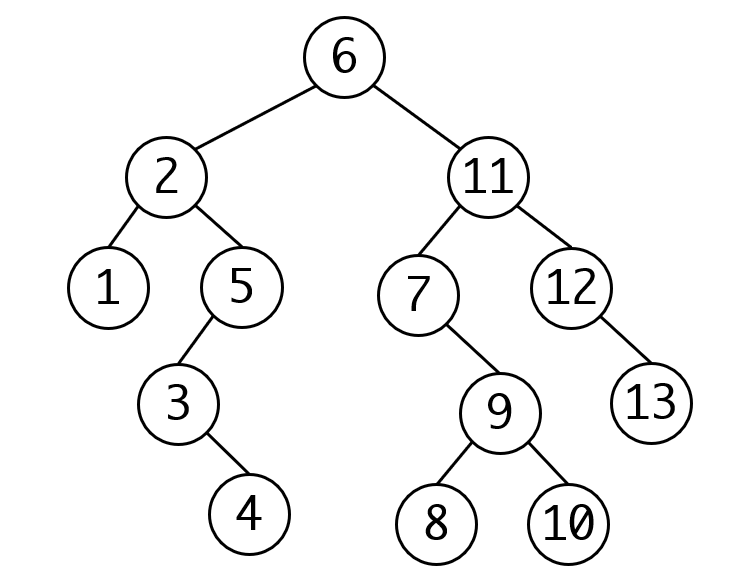
这个性质可以很方便地在搜索树里进行搜索，比如我们要在上面一棵树上寻找8的节点。可以从根节点往下找。

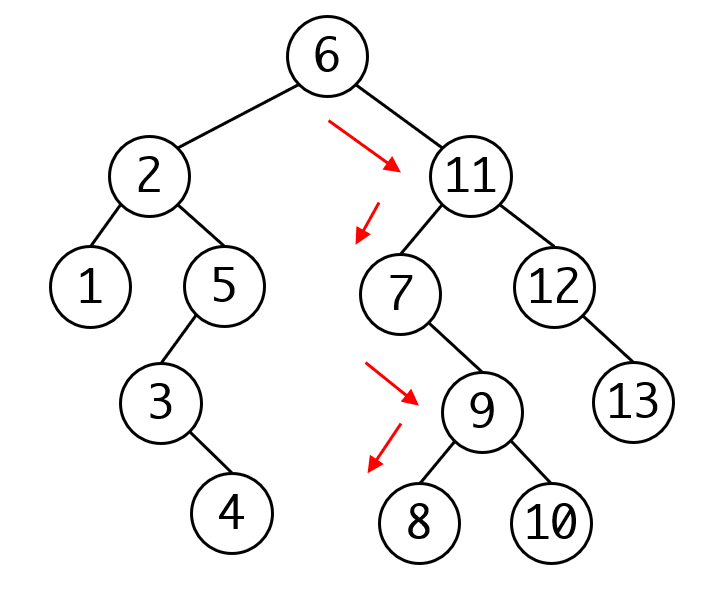
所有节点都可以像这样向下搜索，而如果搜索到叶子节点都没有找到，搜索就失败了，说明这棵树里没有对应的节点。

这也是搜索树名称的由来——这种数据结构就是用来进行搜索的。

搜索树的搜索的次数等于树高，因此搜索复杂度为 $O(logn)$ 。

另一个从搜索树定义可以推导出的性质是：中序遍历搜索树所得的序列是升序的。这其实非常好理解。因为中序遍历将树划分成依次排列的3块，左子树，根节点和右子树。其中左子树比根节点小，右子树比根节点大。再根据递归定义，可以很容易得出升序的结论。

BST的插入

和把大象关入冰箱一样，向BST中插入一个节点的操作也有两步：

现在的问题是，如何找到插入的位置。实际上对一棵BST插入新元素，我们一定将其放在叶子节点处，这可以很大程度上简化逻辑。

因此我们的做法很简单，和搜索一样向下搜索，直到搜索失败为止，搜索路径上的最后一个节点就是我们要插入的位置。此时我们需要把待插入节点放到这个节点的左或者右子树上：

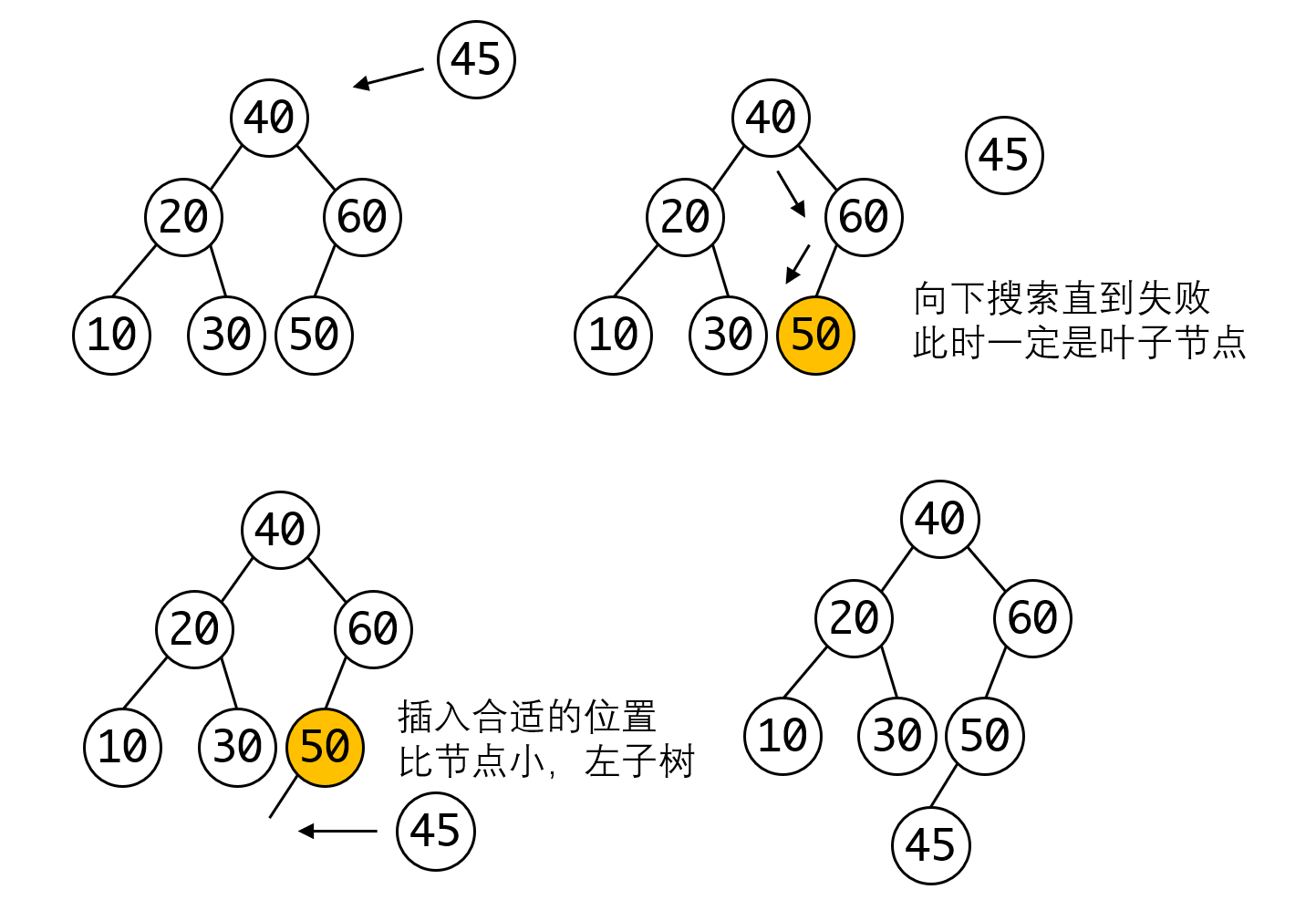
显然这个操作的复杂度是 $O(logn)$

与插入节点相比，节点的删除则相对复杂，因为我们无法假定被删除节点的位置，根据节点删除的位置，可以分成三种情况，前两种情况比较容易理解：

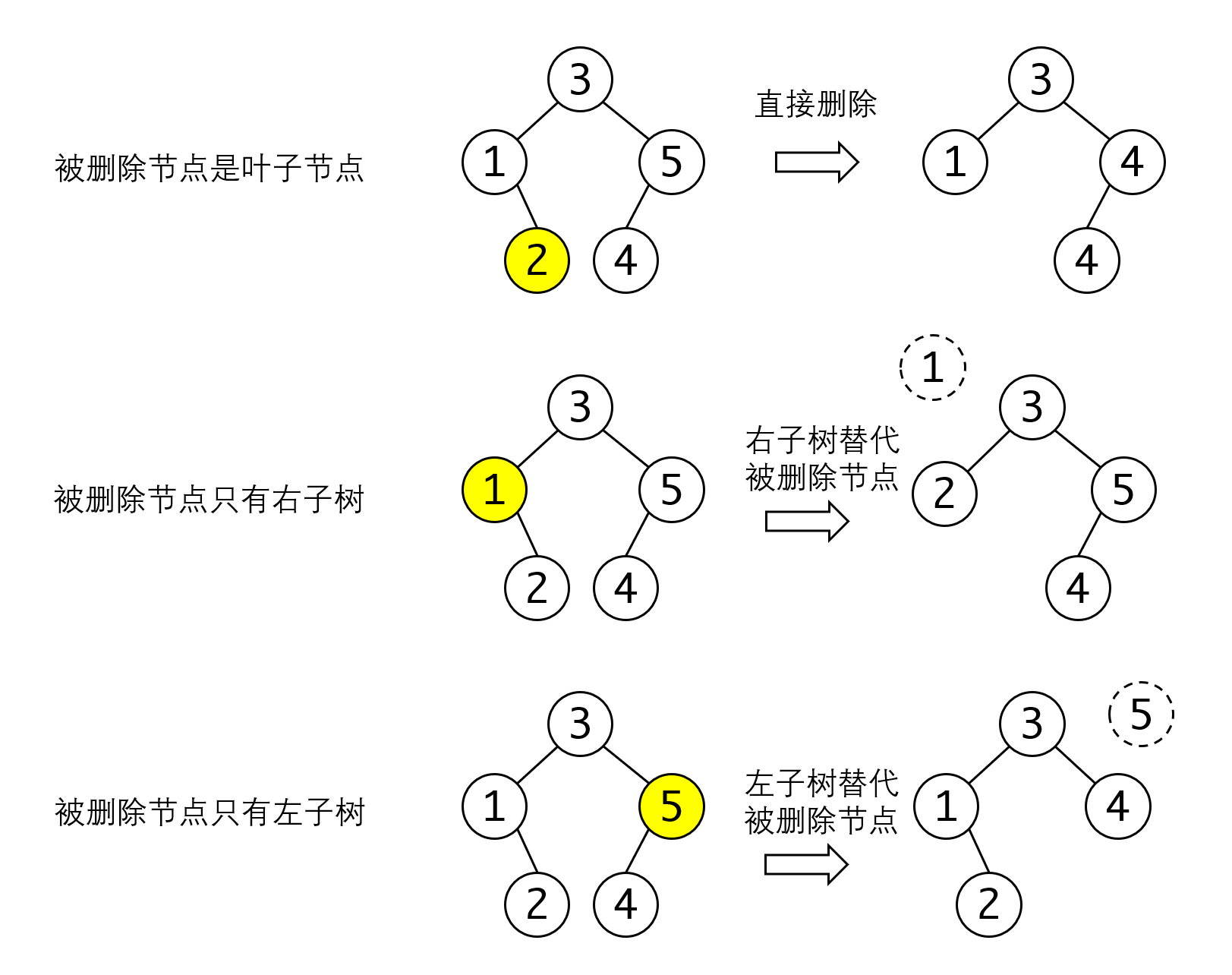
第三种情况节点的左右子树都存在比较复杂一些：

这种情况我们无法直接删除该节点，因为我们有两个子树需要放入，但只多出了一个空位。这里我们可以按我们最擅长的逻辑：把问题转为已知解决的问题进行处理。我们先看处理的逻辑，再看为什么这种方式可行：

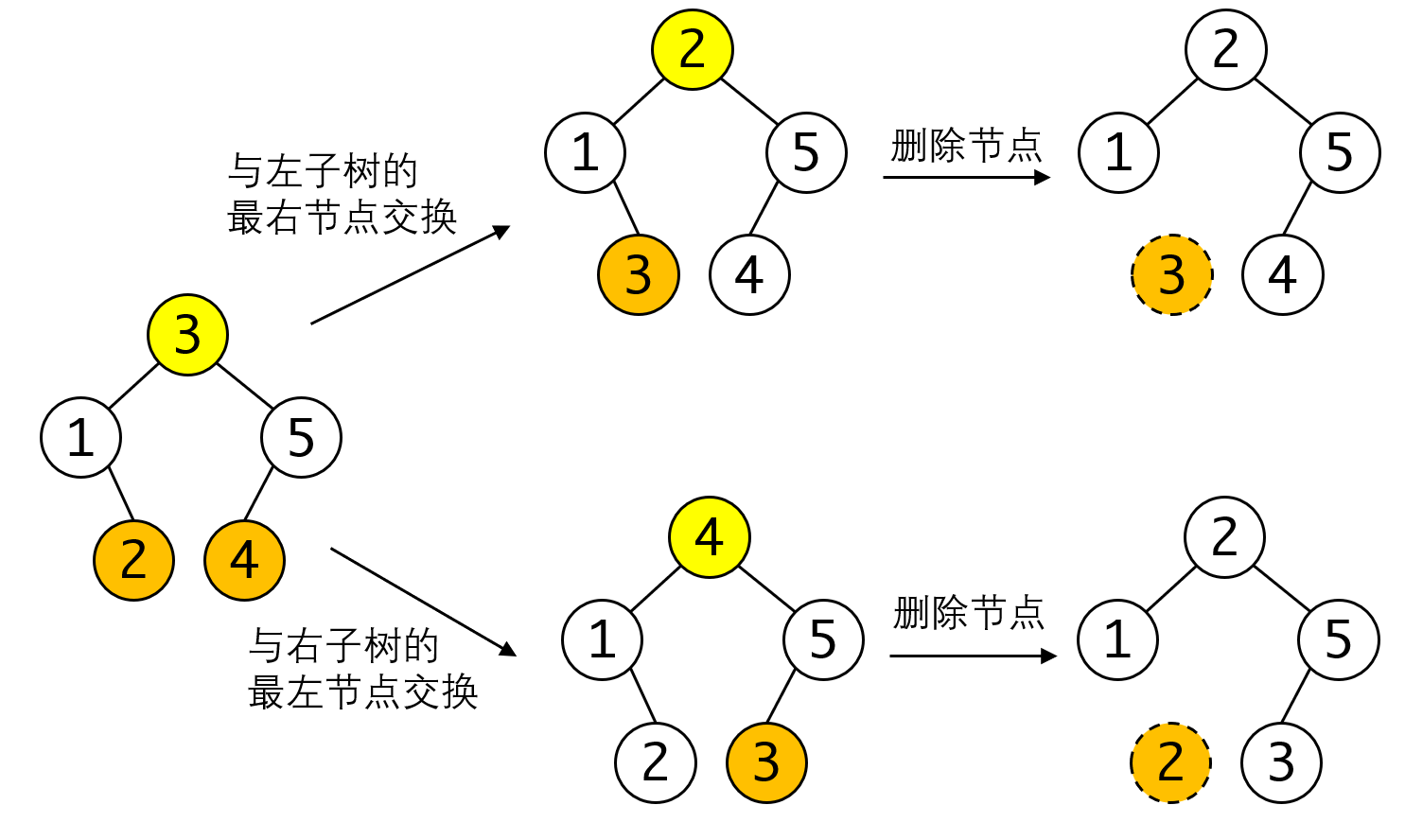
那么为什么这种做法可以解决问题呢？这个问题要分两个问题来看：

第一个问题就要看左子树的最右节点和右子树的最左节点究竟是什么？我们看中序遍历的次序：

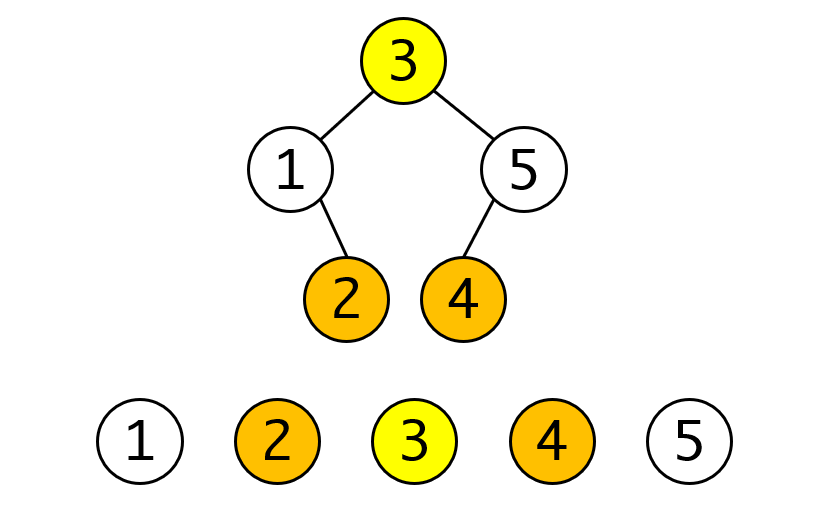
我们可以发现这两个节点是正好是是中序链上与待删除节点相邻节点，因此与这两个节点进行交换，再删除节点并不会改变中序遍历的次序，也就维持了BST树的结构。

实际上左子树的最右节点就是左子树的最大值节点，也就是离根节点最近的左节点。而右子树的最左节点就是右子树的最小节点，也是离根节点最近的右节点。

第二个问题是为什么这两个节点可以用1、2的方式来解决。也就是为什么这两个节点不可能也有两个子节点？

这也是很容易理解，因为左子树的最右节点一定没有右子树（否则他就不是最右的），而右子树的最左节点一定没有左子树（否则他就不是最左的）。

因此我们3的处理方式是可行的，因此完整的删除逻辑如下：

从这个例子我们也可以看出，相同的数据，满足BST要求的二叉树有很多种。

上面三种删除的情况里，前两种情况的复杂度可以认为都是 $O(1)$ ，第三种情况则最大可能遍历整棵树，因此复杂度是 $O(logn)$ 。