栈和队列算法

栈和队列有一个很大的共同点：他们都是容器，容器就意味着可以存东西。 从这个角度看，栈和队列来解决问题的思路非常简单，把当前的状态或者数据记录下来，以备后续使用。

所不同的是，根据栈和队列的特点。栈是先进后出（FILO）的，因此从栈里拿出来一定是离他最近被放进去的元素。而队列具有保序性，放进去是什么样，出来也是什么样。

请大家带着这样的概念，看下面问题的解决。

栈算法

栈后进先出的特点让他非常适合进行回溯。大家可以针对下面的算法思考下，究竟回溯的是什么？

括号判断

要求：有一串字符串，请你判断该字符串的括号是否是合法的。合法的定义是同一种括号只能跟自己匹配。

例如，以下情况是合法的：

[[()]{(){{}}]
{}()
[{()}]

以下情况则不合法：

][
{)
{([)]}

分析：问题的关键在于，当我们遇到一个左括号时，我们无法知道他是否是匹配的，必须等他的右括号出现时才能判断。所以当我们遇到一个左括号时，我们必须存起来等待他的右括号。而对于右括号，必然和最近的一个左括号进行匹配。如果可以匹配，则合法，否则就是非法。

整个过程类似一个消除游戏，左括号和右括号遇到一起之后可以消去，最后消除到空则说明匹配成功：

如此我们可以用栈来存放读入当前缓存的左括号，遇到左括号入栈，遇到右括号则跟栈顶的括号消除，能消除则继续，否则就匹配失败。

思考下

匹配错误的可能性有哪几种？

Undo & Redo

撤销和重做是几乎所有编辑器都带的功能，撤销是很容易想到用栈解决的问题。

基本的操作，每做一个操作，就把一个逆向的操作到栈里面。当用户按下撤销键时，就从栈中弹出一个操作，并应用。

例如一个文本编辑器：

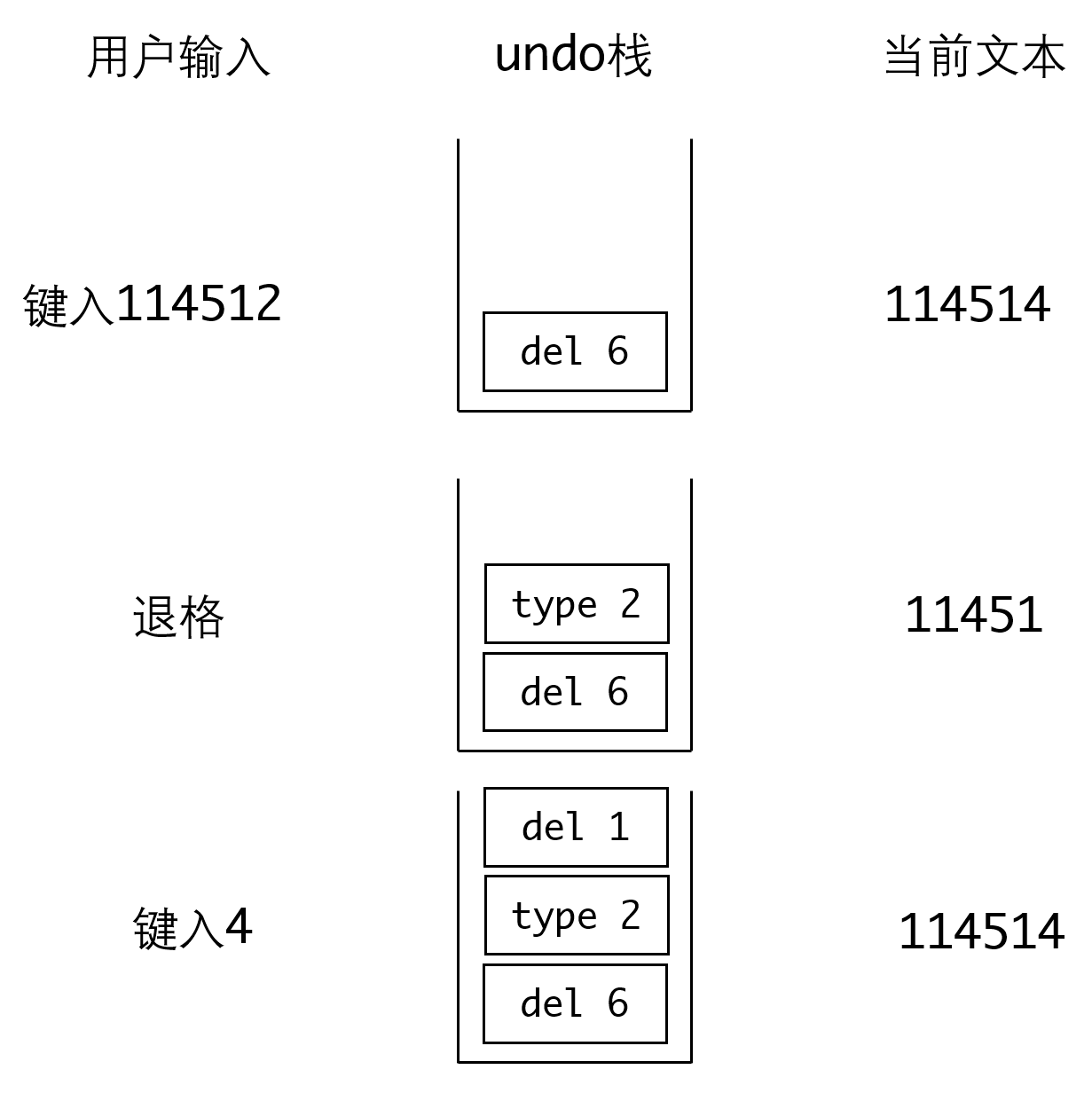
1. 当你输入114512时，栈里放入这个操作的逆操作：del 6，表示删除6个字符。
2. 当你输入退格，删掉2时，栈里放入逆操作：type 2，表示输入一个2。
3. 当你输入4时，栈里放入逆操作：del 1，表示删除一个字符。

撤销的过程则是不断弹出栈元素并执行的过程。

1. 第一次撤销，从栈中弹出del 1，删除1个字符，得到11451
2. 第二次撤销，从栈中弹出type2，输入字符2，得到114512
3. 第三次撤销，弹出del 6，删除6个字符，得到空串

那么大家思考下：Redo要怎么做？

走迷宫

如果回顾下我们人类走迷宫的方式，最符合直觉的方式是这样的：遇到岔路口就选一条路走并打上标记。 如果遇到死胡同，就回到上一个路口，选一条没走过的路继续走下去。如果某个岔路口已经全都走过了，那么就向上再退一层，回到上一层。

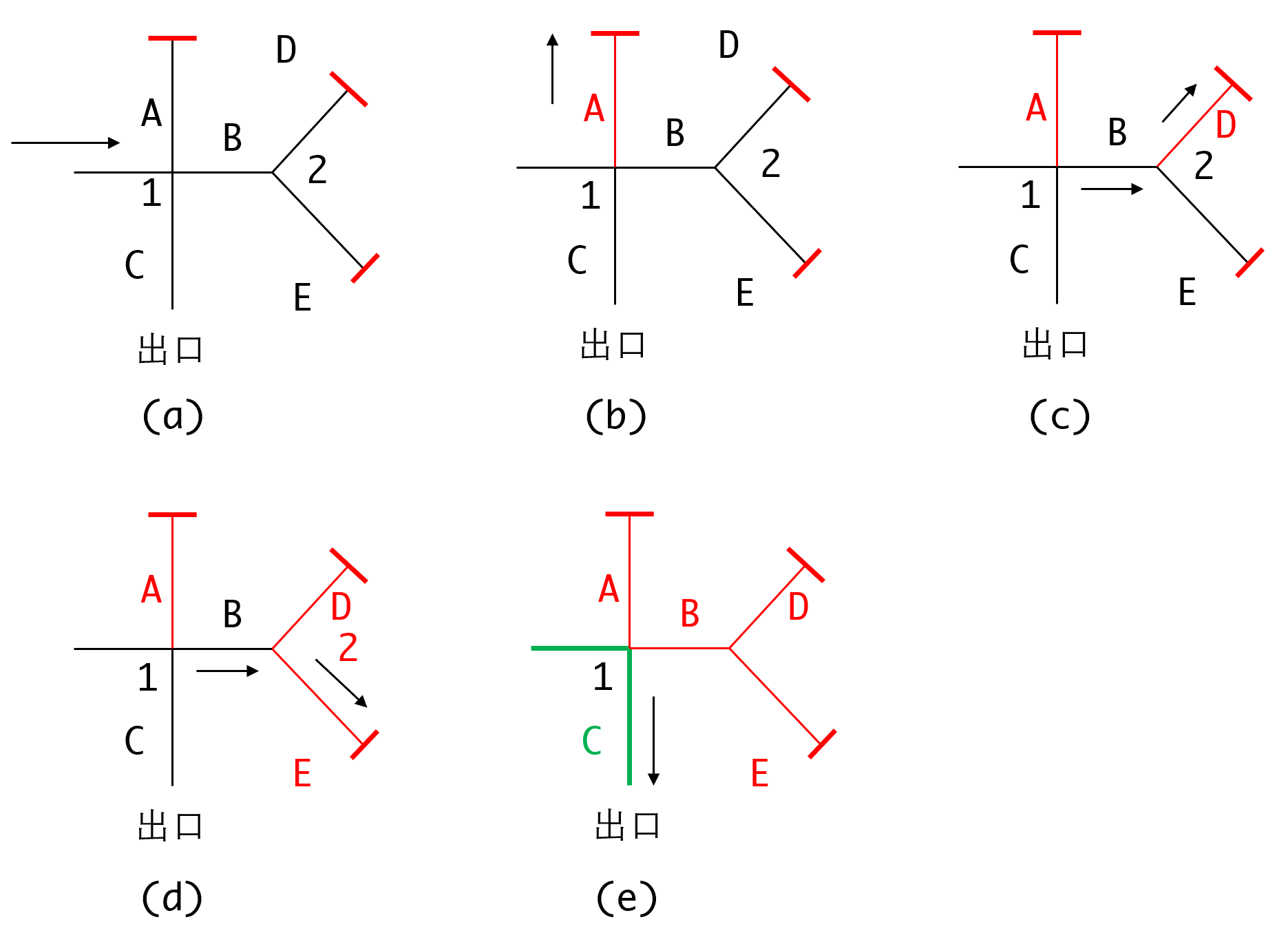
看这张图，一共有两个岔路口，1有ABC三条路径，2有DE两条路径。 人类走迷宫的方式是这样的：

1. 走到岔路口1，任意选择一条路径，假设都按顺时针选，这里就先选A。
2. A走到死胡同，返回岔路口1。
3. 走B，到达岔路口2，选择路线D。
4. D走到死胡同，返回岔路口2，选择路线E。
5. D也走到死胡同，返回岔路口2，发现岔路口2已经没有其他路线了，继续返回上一个岔路口1。
6. 选岔路口1的最后一条路径C，找到出口。

请注意整个过程中，如果我们遇到死路，总是返回上一个岔路口，直到这个岔路口所有的路径都已经被遍历完毕之后，我们再返回这个岔路口之前的一个岔路口。

这非常符合我们人类的习惯，毕竟如果我们每次都返回第一个岔路口，从这个岔路口开始寻找新路线，不仅会增加我们返回的路线成本。我们也很难记住那么多路径。

如此我们可以发现，我们总是返回上一个，除非走不下去，才会返回之前的路口。 也就是说如果我们遇到岔路口的顺序是：

1 2 3 4 5

那么我们往回走的时候，会先回到5，再回到4，以此类推。显然这也是一个后进先出的顺序。

将地图转成比较好讨论的$width\times height$的矩阵，我们也可以让计算机像我们一样走迷宫：

1. 如果栈顶格子有相邻的格子可走，就选其中的一个格子入栈，并给这个格子打上标记，表明已经走过
2. 如果栈顶格子已经没有相邻的格子可以走，就弹出他。
3. 重复这两个过程，直到找到遇到出口（成功）或者栈空（失败）。

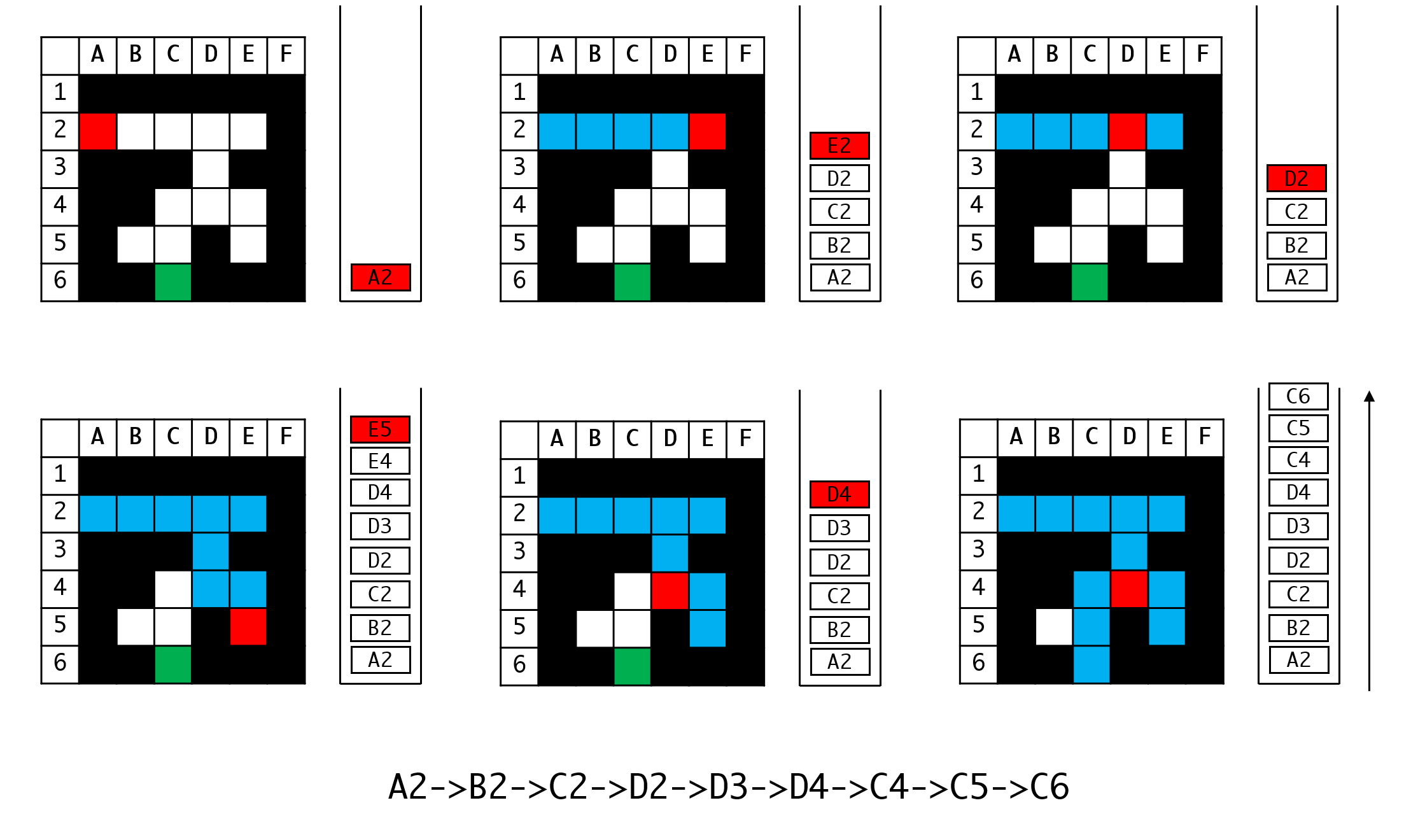
请注意这里我们并不特别记录岔路口，而是把每个格子都当作岔路口，这样的好处是我们不用区别对待某个格子，可以让代码逻辑最简化。

1. 从A2到D2这一条段，每个格子都只有一个可能的选择，我们依次入栈，到D2，产生了岔路，我们从上方开始按顺时针选，此时应选E2。
2. 一路走到到E2
3. E2是死胡同，于是我们弹出E2，此时栈顶是D2。
4. D2只有相邻的D3可以选，到D4之后，从上开始顺时针选，走E4并一直到E5。
5. E5是死胡同，弹出E5，栈顶是E4，但此时E4也没有其他路径可以走，继续弹出，到D4。
6. D4还可以走C4，到C5，按从上开始顺时针方向选，走C6，抵达出口。
7. 此时栈底到栈顶的各个元素，就是我们所需的路径。

这种不把一条路走到黑就不会回头的算法，我们称为深度优先遍历或深度优先搜索（DFS）。对于深度优先搜索，总是可以用栈来实现。

表达式求值

考虑下面的表达式求值：

1+2*3=

如果让大一的你来编写代码，你十有八九只能这样计算：

1+2*3
=(1+2)*3
=3*3
=9

但小学2年级的学生都知道，先乘除，后加减，正确的计算是：

1+2*3
=1+(2*3)
=1+6
=7

这是因为我们规定了运算符的优先级，也即当你看到1+2时，你并不能立刻计算，只有在2后面的运算符与前面的+同级，或者比+低时，才能计算1+2。

这一问题的解法我们可以使用两个栈，一个记录操作数，另一个记录运算符。

算法的规则如下：

1. 遇到操作数就放入操作数栈
2. 当遇到操作符时，与栈顶元素对比
3. 如果当前操作符的优先级比栈顶元素高，将操作符入栈
4. 如果当前操作符的优先级比栈顶元素低，则取出两个操作数和操作符，执行计算，并把结果放入操作数栈
5. 重复上述过程，直到操作符栈空为止，此时操作数栈的值就是表达式的结果。

为简化代码处理，我们用#将表达式包裹起来。将#作为最低优先级。停机条件则可以设置为栈底只剩#且遇到读到#。

我们看一下计算#1+2*3^2#的过程，其中3^2表示计算3的2次幂，我们规定运算符的优先级为# < + < * < ^。

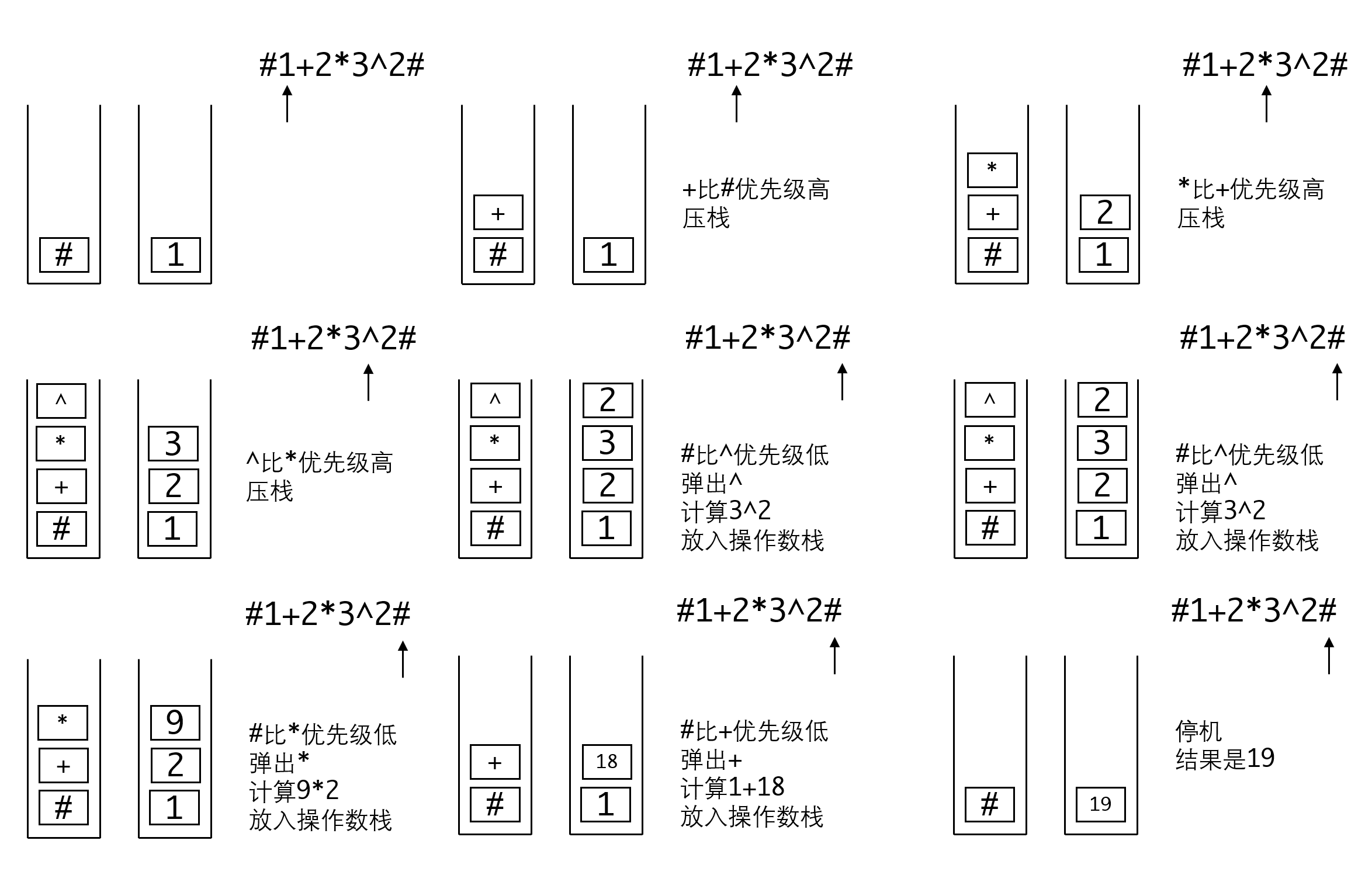
括号要如何处理？

我们可以观察括号的行为：

1. 括号里的计算优先级高于所有计算
2. 左右括号内构成一个完整的算式

根据这点，我们可以有如下选择：

递归：遇到括号时，将与之匹配的括号内部当作一个算式来递归求解，结果放入操作数栈。

对括号特殊处理，我们可以人为规定：

1. 遇到左括号一定入栈
2. 左右括号的优先级都最低
3. 左右括号相遇则一起消去（当前指针为右括号且栈内是做括号时弹出左括号，同时指针后移）

函数调用、递归与栈

如果对上面括号匹配和走迷宫认真思考过的话，你会发现：递归也能解决这些问题。

例如括号匹配可以用这样的算法来解决：

一个括号字符串是否匹配取决于：
1. 第一个左括号，是否存在与其匹配的右括号
2. 在这组匹配的括号内部的所有左括号，是否存在预期匹配的右括号

以({[]}[])为例，他能否匹配的充要条件是

1. 最外层的(存在与其匹配的)
2. 这层匹配的中间{[]}[]里的每个左括号，都存在与之匹配的右括号

这显然是一个递归算法。

同理迷宫寻路算法也可以用如下的递归式来叙述：

当前格到出口的一条路径为周围任意一个到出口的路径，加上当前格。

实际上你还能找到很多例子，包括我们后面的二叉树的递归遍历、图的深度优先搜索等等。

这就让我们不能不思考一个问题：为什么栈能解决的问题和递归能解决的问题有如此多的相似性？

原因在于递归或者说函数调用，本质上是对栈的一种应用——你还是在使用栈，只不过你看不到。

我们先看一个普通的函数调用过程：

int square( int x ){
    int y = x*x;
    return y;
}

int square_sub( int a, b ){
    int x = square(a);
    int y = square(b);
    return x-y;
}

int main(){
    printf("%d\n",square_sub(1,3));
    return 0;
}

代码在内存里顺序存放，通过pc指针来指向当前执行的指令，普通指令执行后会把pc++，令其指向下一条语句。

但当其中涉及函数调用时，情况就会变得复杂，因为我们需要记录当前的pc指针，以供函数返回时恢复。这必须借助调用栈来实现：

1. 当遇到函数调用时，将pc+1放入调用栈，然后pc指针指向被调函数的开始位置
2. 当函数返回时，从调用栈中弹出栈顶元素，并用它恢复pc指针

整个调用的过程入下面的图：

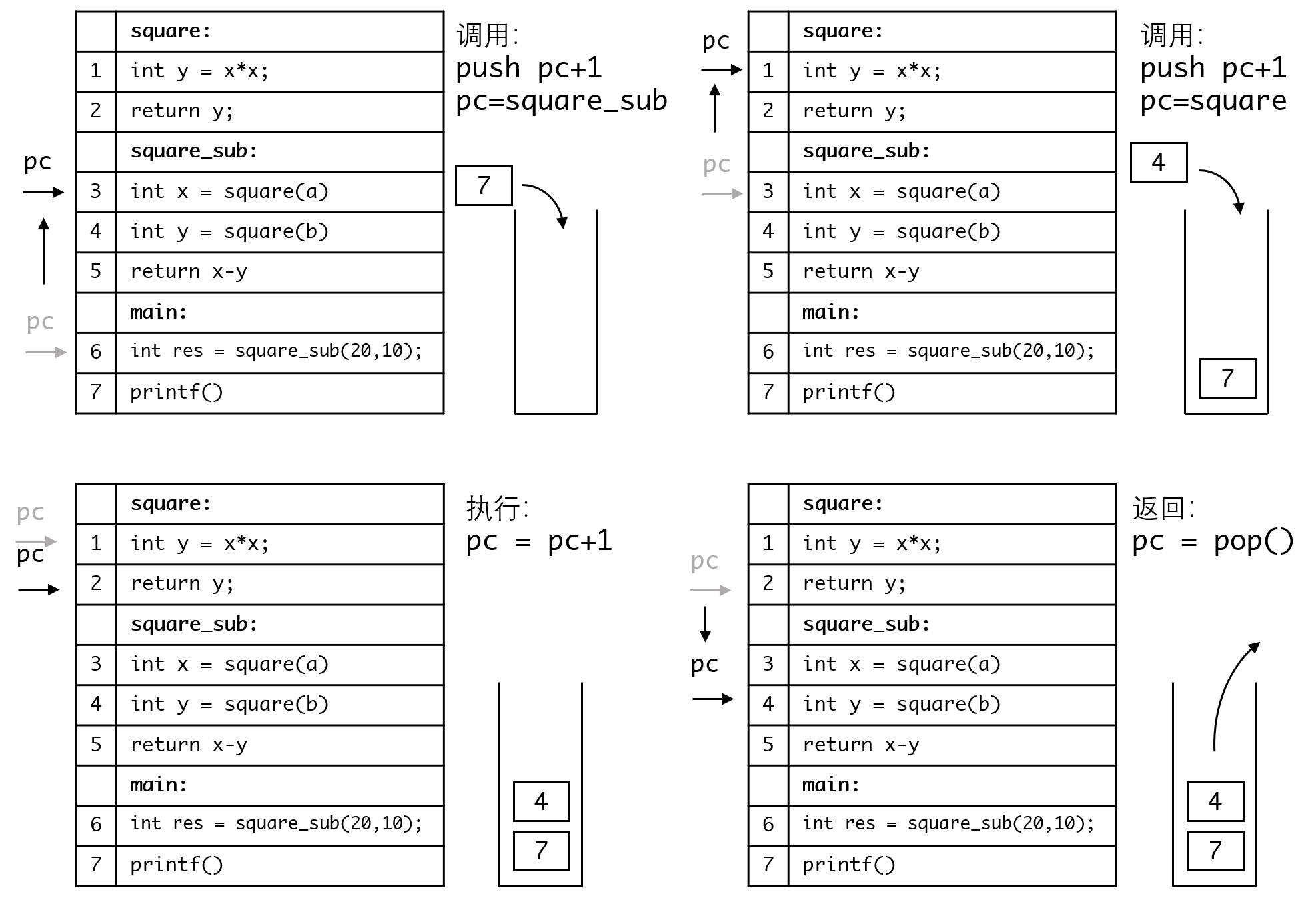
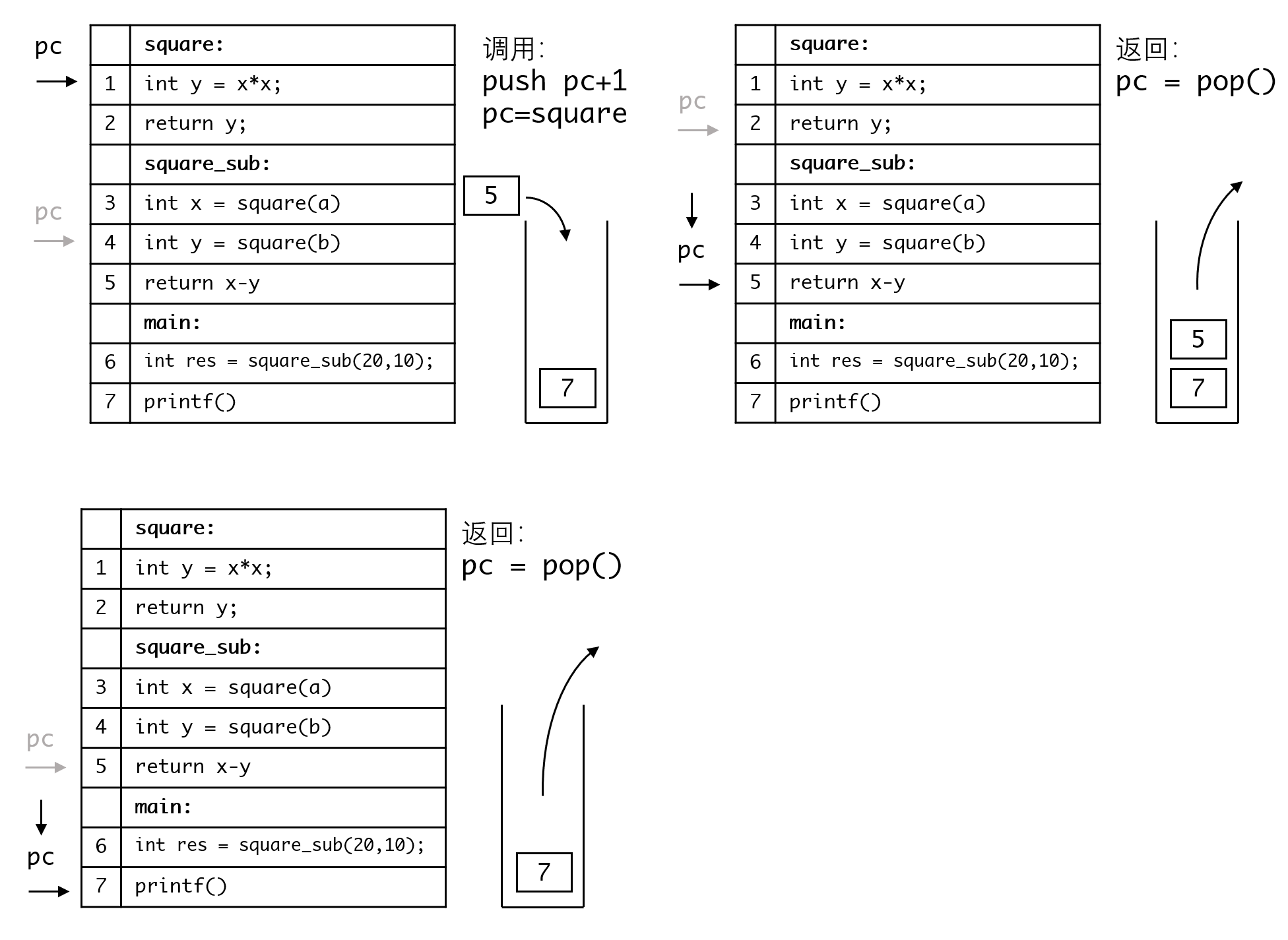
理解了这个，再理解递归也就不难了，我们以递归求阶乘为例：

int factorial( int n){
    if( n == 1)
        return 1;
    int r = factorial(n-1);
    return r*n;
}

int main(){
    printf("%d\n", factorial(3));
    return 0;
}

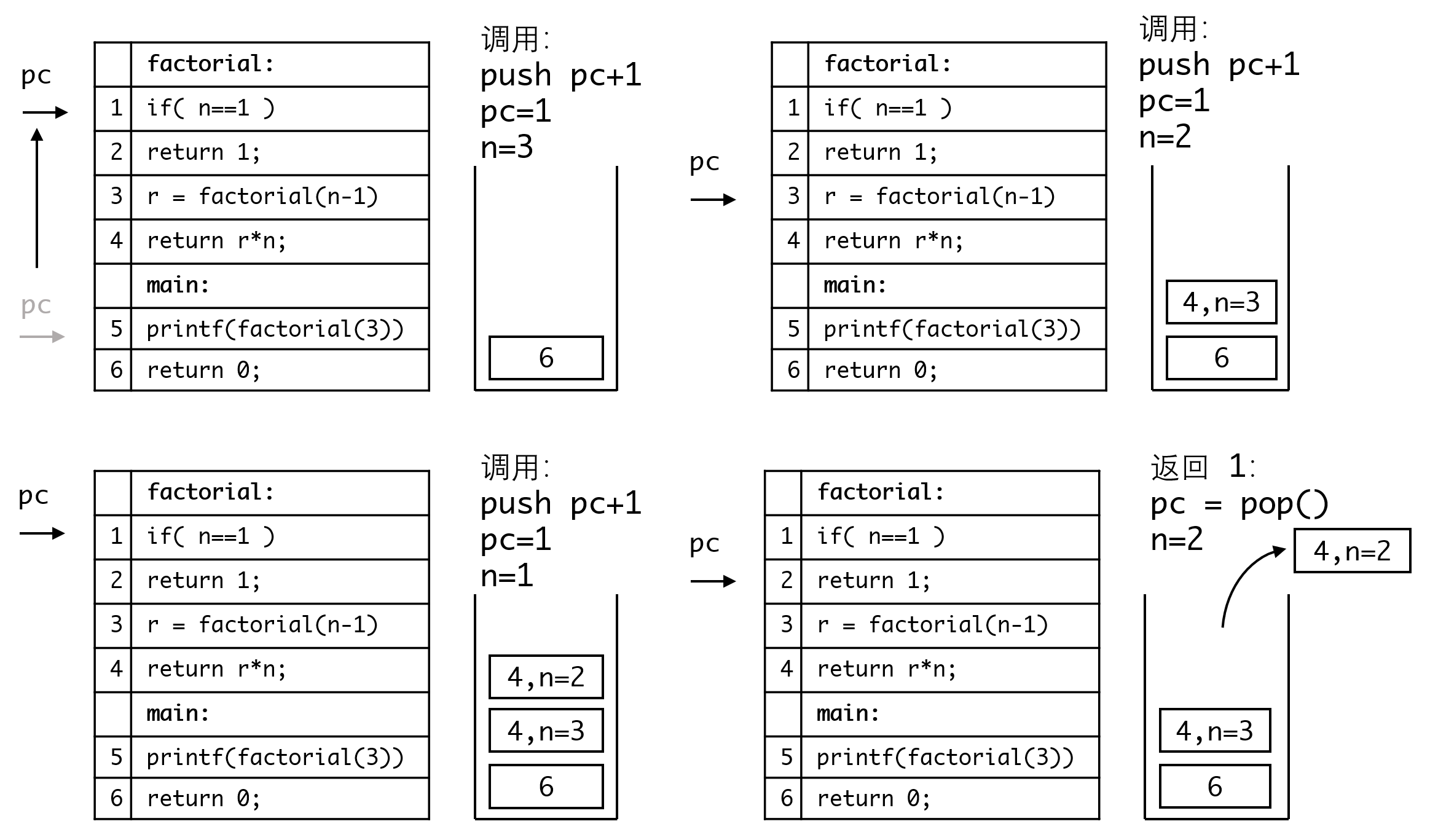
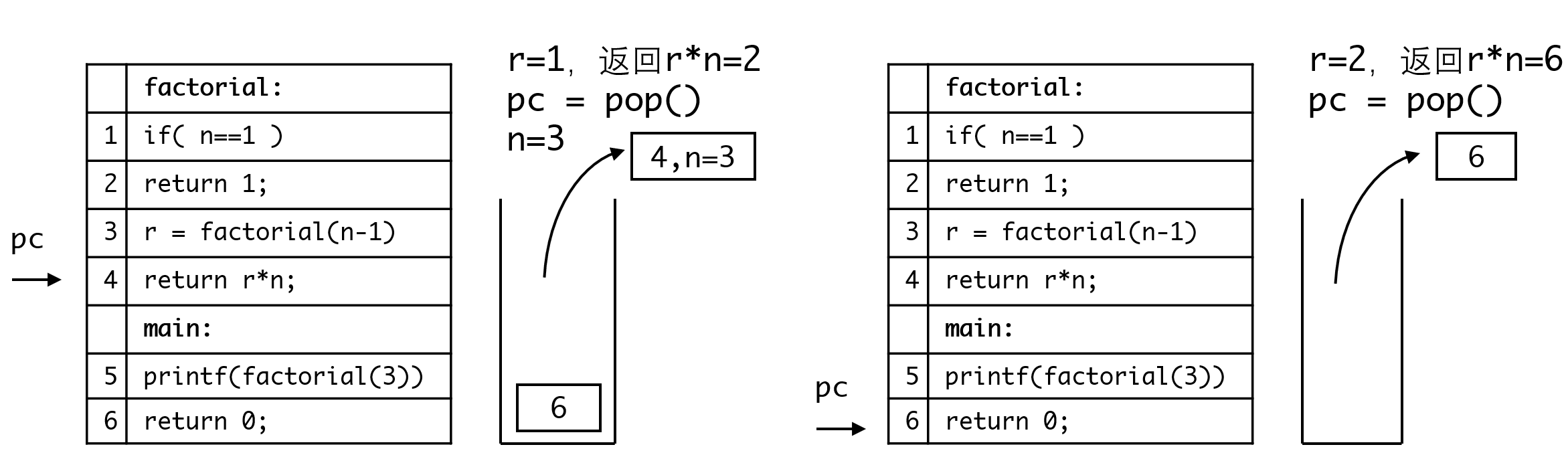
调用栈除了记录pc指针的信息，还要记录局部变量的值，因此我们可以认为压栈的数据除了pc之外，还包括对应的局部变量。

这样我们相当于缓存了当前的状态，直到递归调用的函数返回，再继续执行。 如果我们在main函数里以更大的参数调用factorial函数，也只不过是调用栈多增加了几层罢了。

你明白了吗？

你现在理解为什么我们说：

1. 局部变量不用清理，会自动回收
2. 局部变量出函数之后就不能再访问
3. 递归调用的层次不宜过深
4. 函数内不要定义很大的局部变量或者数组

这些的原因了吗？

队列

队列和栈不同的是，队列是保序的，所以队列基本是按顺序缓存的唯一指定数据结构。

操作系统调度

生活中最常见的队列是排队，当服务的速度赶不上人流的速度时，就会出现排队的情况了。

计算机中也有与之类似的情况——当数据无法被及时处理时，就需要队列来缓存他。

这种例子在计算机里比比皆是，最典型的比如操作系统的进程调度。在一个操作系统中，会同时运行非常多的进程，要保证所有进程能够公平地获得运行的时间，操作系统一般使用队列来实现：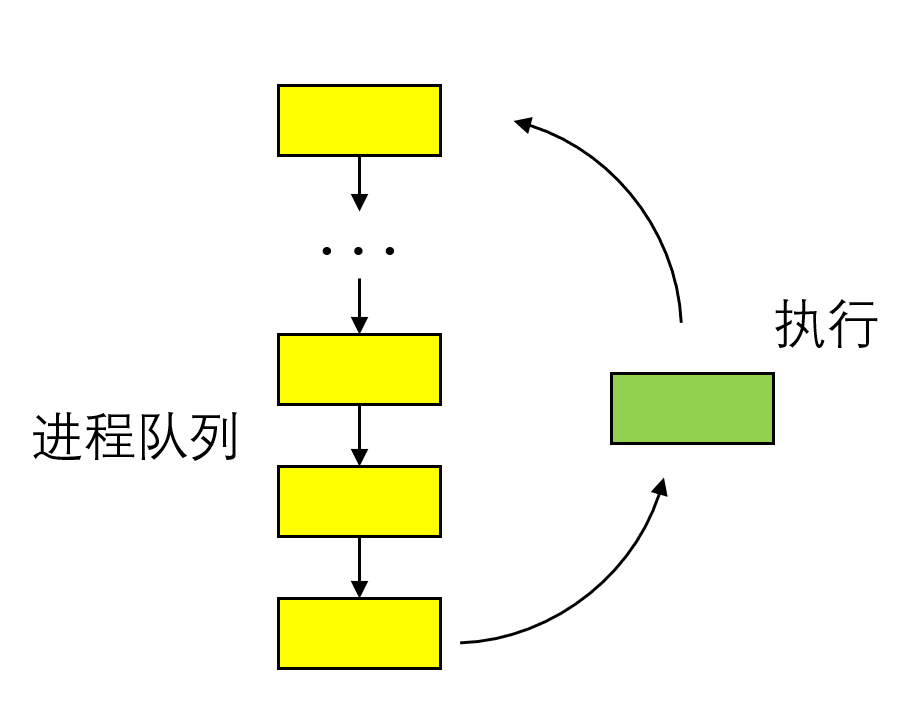

每次从队头取出一个进程，运行指定的时间（时间片）后，暂停这个进程并将其放入队尾。 这样保证每个进程都能获得大致相当的运行时间。当然真实操作系统的进程调度远比这复杂。 还要涉及优先级等问题，但大体思路是相同的。

此外操作系统的消息传递，也采用消息队列的方式。像windows里的每个窗口，都有一个消息队列。当用户的操作触发某个消息，操作系统就会将该消息放到对应窗口的消息队列里。窗口的消息处理函数则从队列里取出消息并处理。

我们在windows系统下的每一个操作，比如在输入框里输入内容、点击按钮、移动鼠标、所有的这些操作，底层都是由一个个消息来传达的。

种子填充算法

填充算法是图形学中非常常用的一种算法。

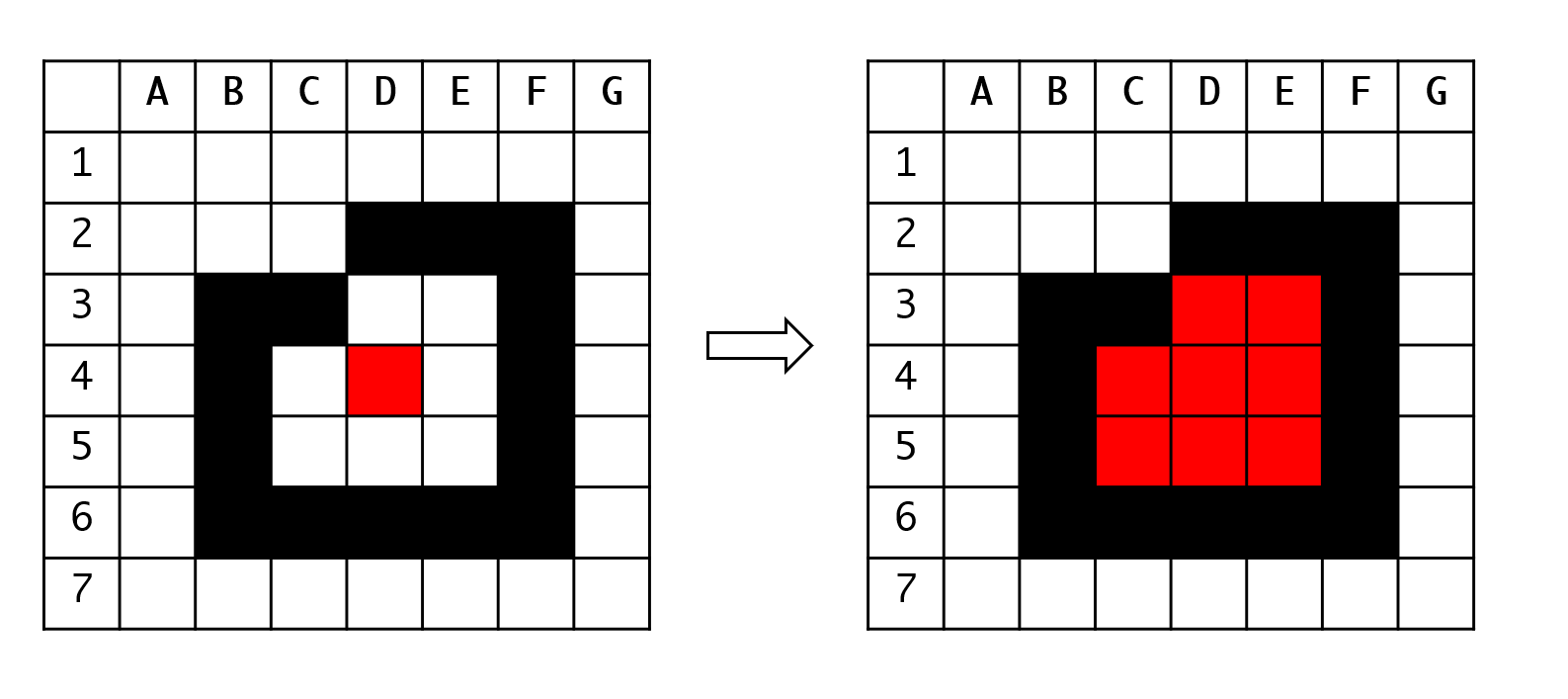
给定某个封闭图形中的一点，要求填充这个封闭的图形。这个给定的点就是所谓的“种子”。

这是个很典型的用队列解决的问题，算法的步骤我们可以描述为：

1. 将种子染色并放入队列
2. 从队列头部取一个元素
3. 将这个元素四周可以染色的块——不是边界颜色，也没被染色过——染色，并放入队列
4. 重复2、3直到队列为空

整个流程如图所示：

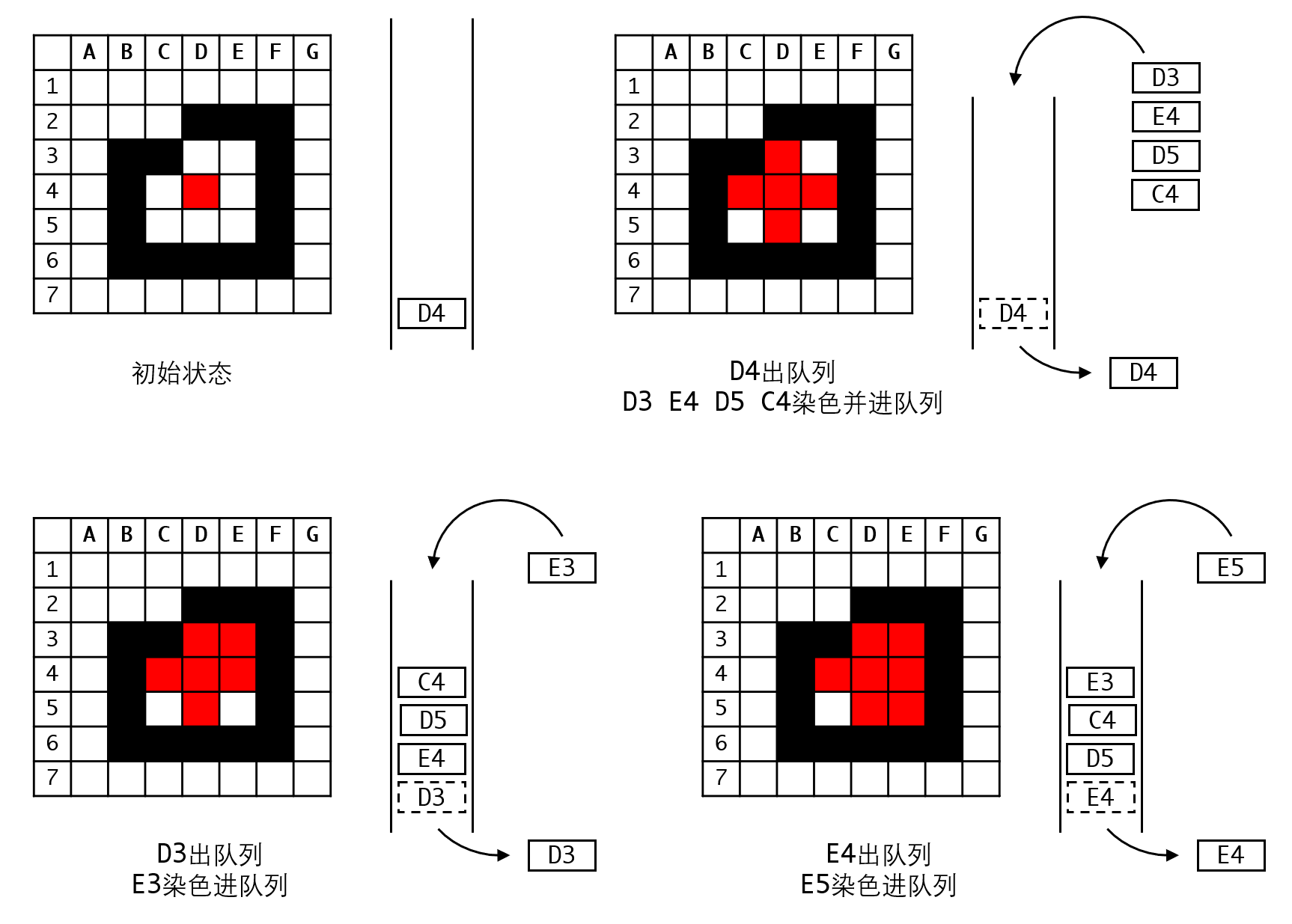
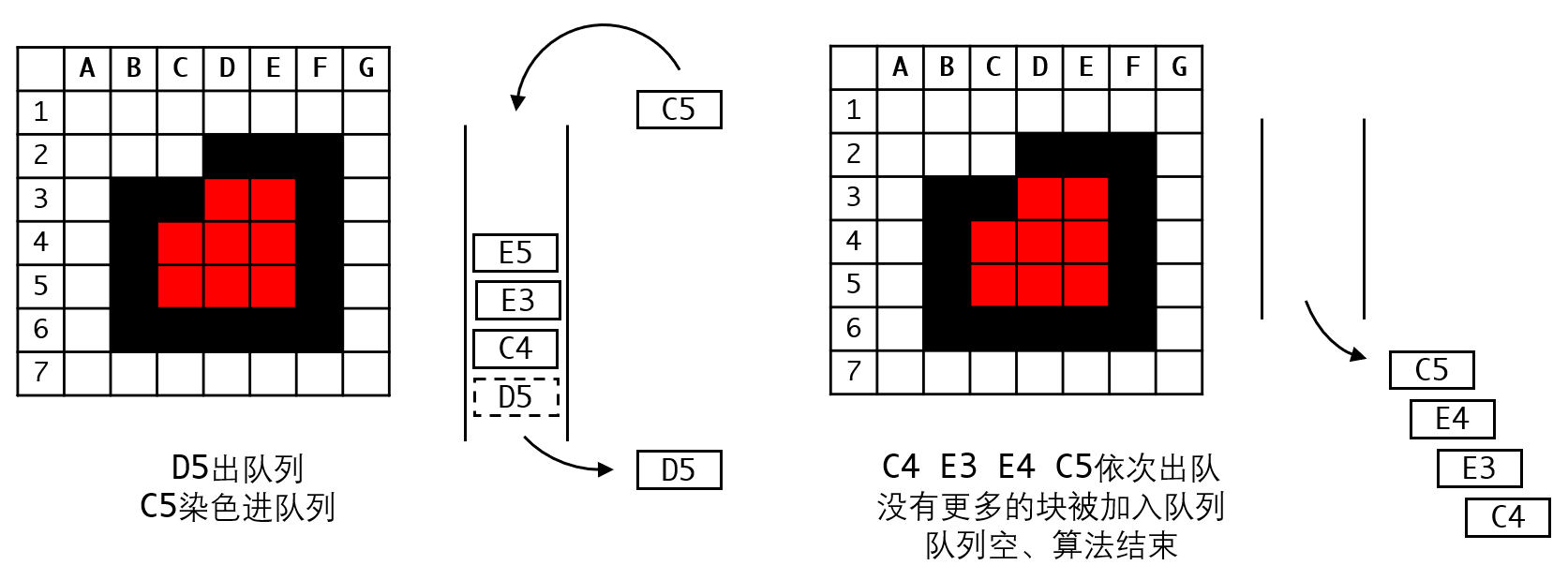
思考一下

1. 为什么我们先染色再进队列，反过来可不可以？
2. SLG战棋类游戏的移动，与填充算法有什么相似的地方，又有什么需要改变的？
3. 相同的思想，还可以应用在什么地方？

我们设想一下，如果要填充的空间比较大的话，那么会是怎样一种填充的次序。

首先被加入队列的是种子周围的四个块。 随着这四个块从队列里出来，他们周围的块是第二波被加入队列的。 以此类推，我们会发现每一波，都离原来的中心点更远一点。

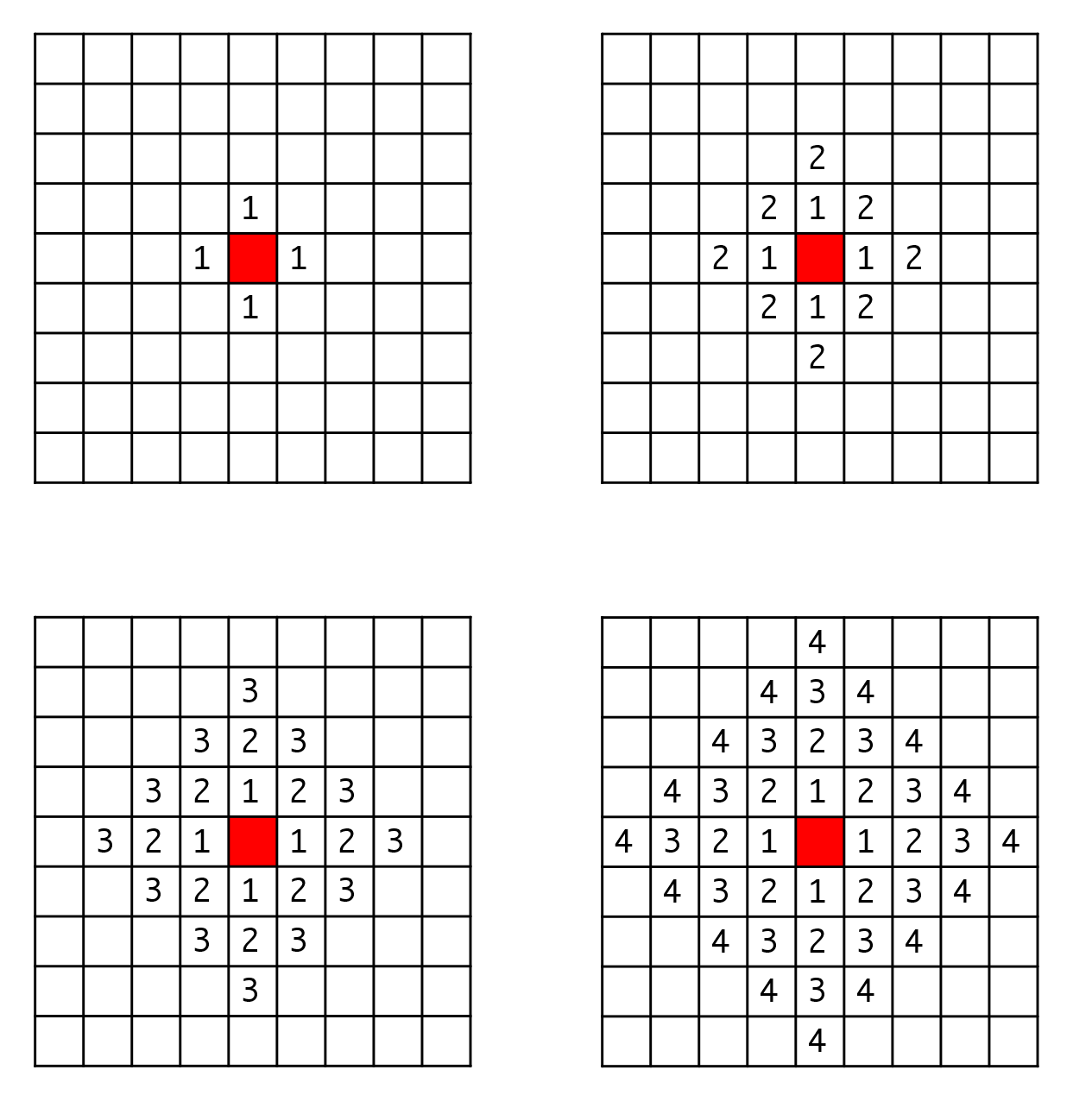
此外我们还可以发现，算法优先处理当前块周围的块，而不是优先走得更远。 我们把这种优先将相邻区块进行处理的算法叫广度优先遍历或者广度优先搜索（BFS）。 对于广度优先搜索，总是可以用队列来实现。