哈夫曼树

“最优”的二叉树

我们考虑这样一个要求：把成绩从百分制转为五级制。这样的题目你们大一就懂得做了：

string hundred_to_five( int grade ){
    if( grade >= 90 )
        return "优秀";
    else
        if( grade >= 80 )
            return "良好"
        else
            if( grade >=70 )
                return "中等"
            else
                if( grade >=60 )
                    return "及格"
                else
                    return "不及格"
}

这里为了让逻辑更复合我们讨论的内容采用了这种写法，实际工作中不要学。

我们可以画出这一过程的判定树（下图a）：

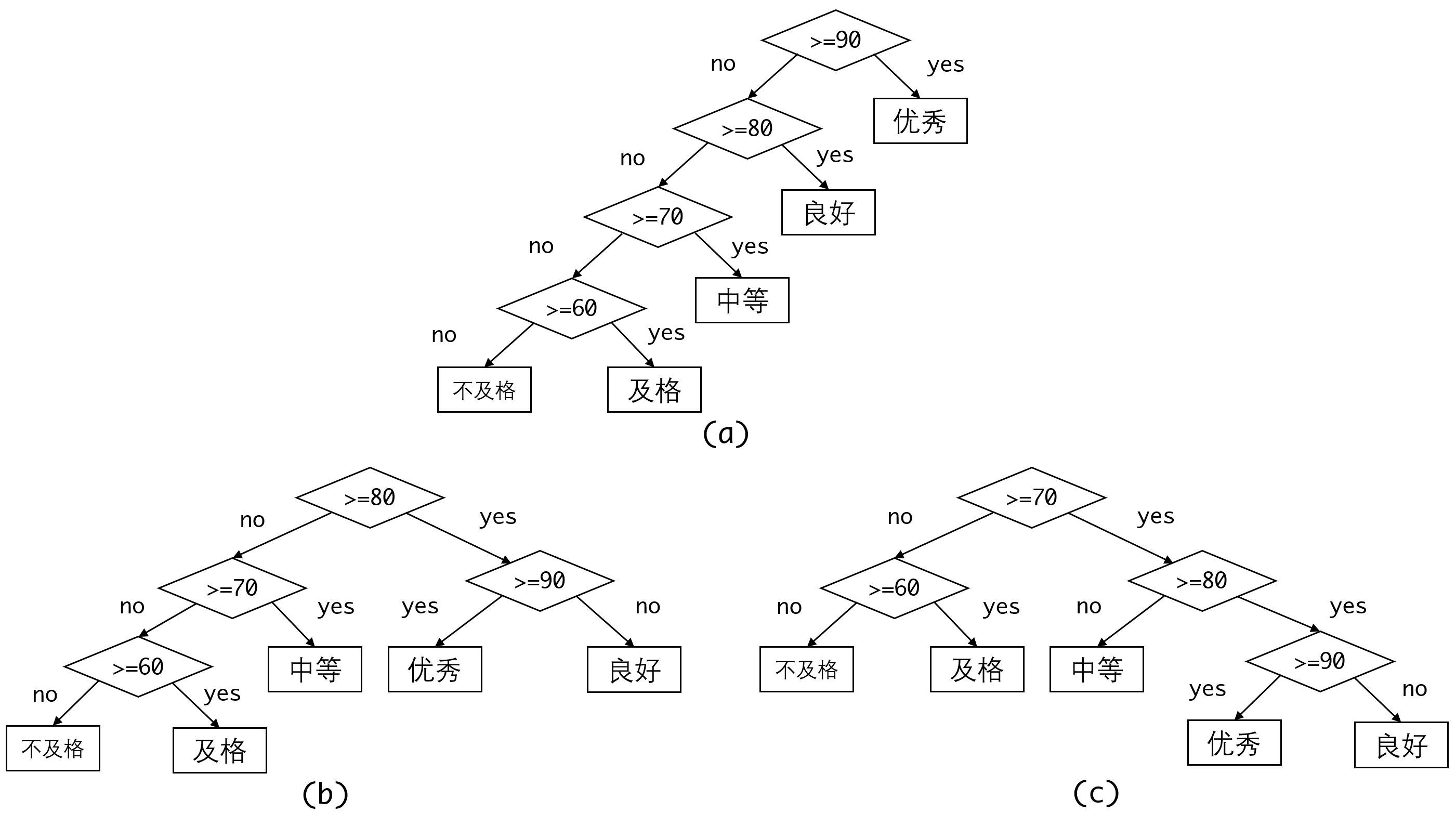
不过这里的逻辑是不唯一的，图b和c也一样可以完成这个逻辑。那么我们很自然的就会考虑，哪种方式的效率是最高的？

需要明确的一点是效率的高低跟分数的分布有关。

这点很容易理解，如果我们班级有N个人，考虑非常极端的情况，全班所有人的分数都不及格，我们可以很容易算出三种逻辑的判断次数：

逻辑	判断次数
a	4N
b	3N
c	2N

如果全班同学的分数都在90分以上，那么我们也有：

逻辑	判断次数
a	N
b	2N
c	3N

这两种情况下，三种逻辑的效率正好相反。所以不同分数段学生的占比决定了处理逻辑的效率。

因此这个问题实际上是：在人数已经确定的条件下，如何得到效率最高的逻辑。

我们注意到，每个逻辑都构成一个二叉树，每个判定节点都是一个非叶子节点（实际上还是一个必然存在左右子树的节点），同时每个判定结果都是一个叶子节点。我们给每个叶子节点一个权重，例如上面的例子中，我们可以用人数作为叶子节点的权重：

分数分布	人数
优秀	2
良好	4
中等	5
及格	1
不及格	1

我们以上面(b)的情况来看，会得到这样一棵树：

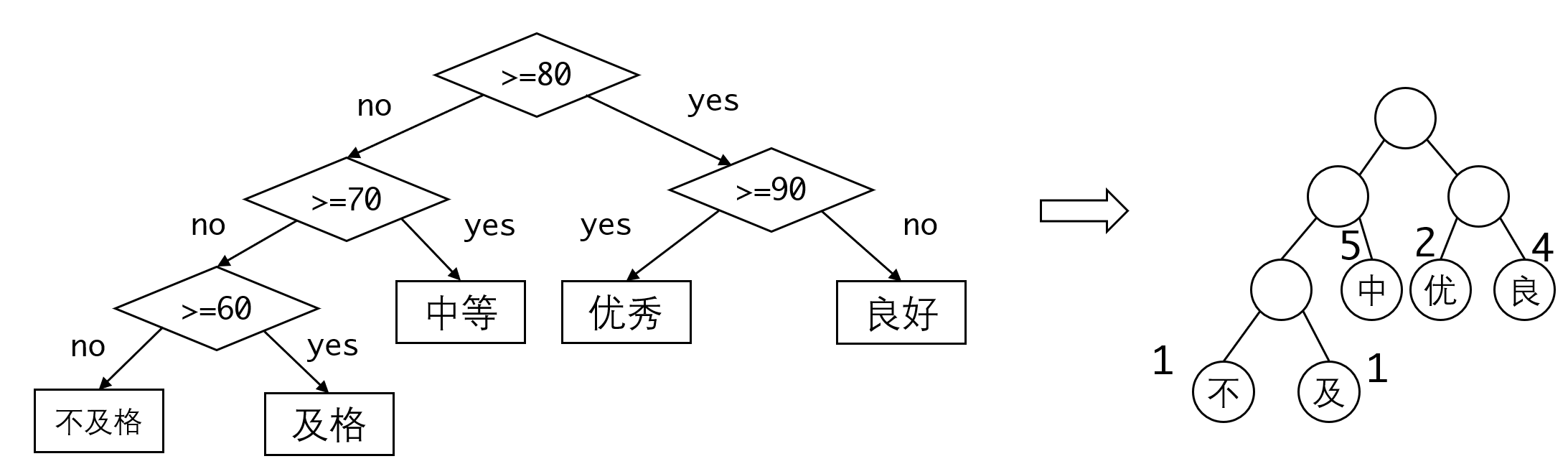
我们再定义带权路径长度：

1. 叶子节点的路径长度为其到根节点所经过的边数。
2. 叶子节点的带权路径长度为路径长度与叶子节点权重的乘积。
3. 树的带权路径长度为所有叶子节点带权路径的和。

以上图为例，我们可以求得每个节点的路径长度和带权路径长度：

叶子节点	权重	路径长度	带权路径长度
优秀	2	2	4
良好	4	2	8
中等	5	2	10
及格	1	3	3
不及格	1	3	3

所以这棵树的带权路径长度为：4+8+10+3+3=28，很显然，带权路径长度就是这个逻辑执行之后得到的总的判断次数，可以定量地表示整个逻辑的效率，带权路径长度越小，判断的次数越少，效率也越高。

我们称这样树为最优二叉树，或者哈夫曼树。

那么我们的问题就转变为：给N个节点，如何构造这样一棵哈夫曼树。

哈夫曼树的构造

我们观察哈夫曼树的形态，很容易看出，越大的数字应该放在越靠近根节点的位置，这样路径长度比较短：

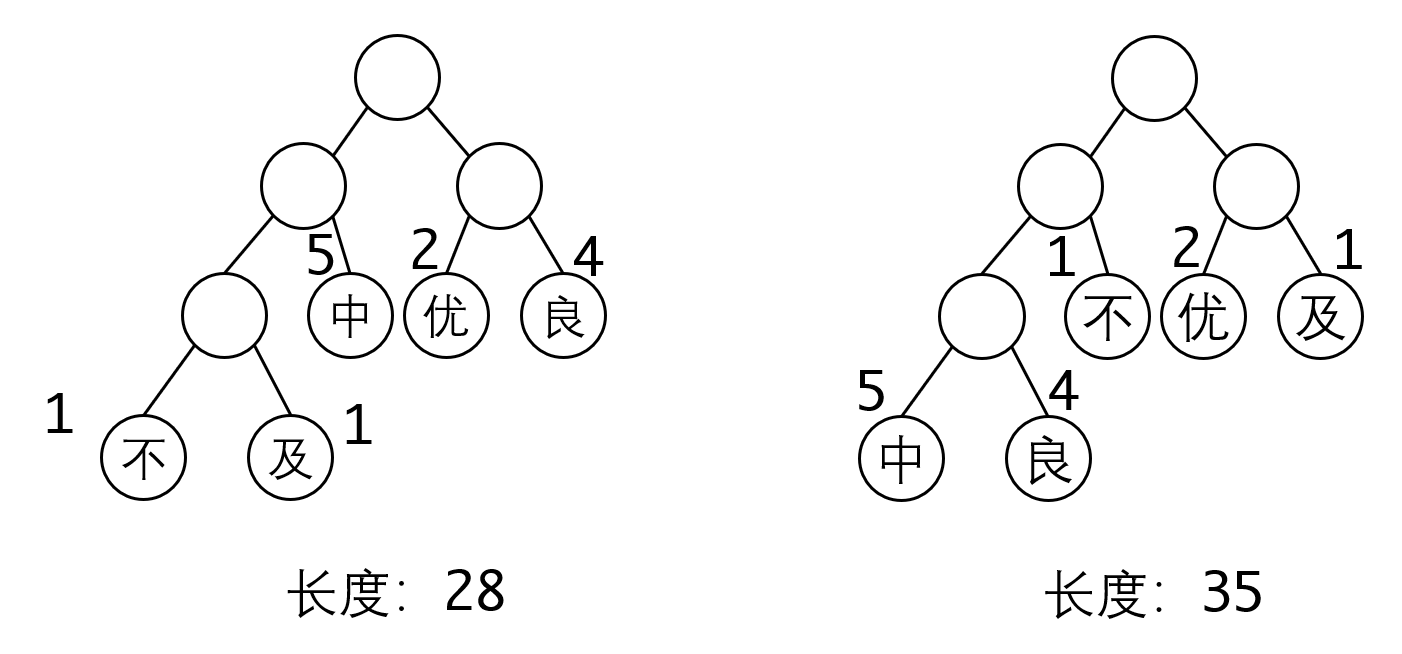
构造这种树的算法是一种很好理解的贪心算法：

1. 将所有的叶子节点放入待选集合S。
2. 选S取出最小的两个节点作为左右子树，构建一棵二叉树，根节点的权为两个节点权之和。
3. 将2中生成的2叉树放入集合`S`，将根节点作为待选节点（也就是说不再考虑叶子节点）。

假设有A B C D E F G这几个节点，他们的权分别是：1 1 4 5 8 9 11，我们看如何构造一棵哈夫曼树：

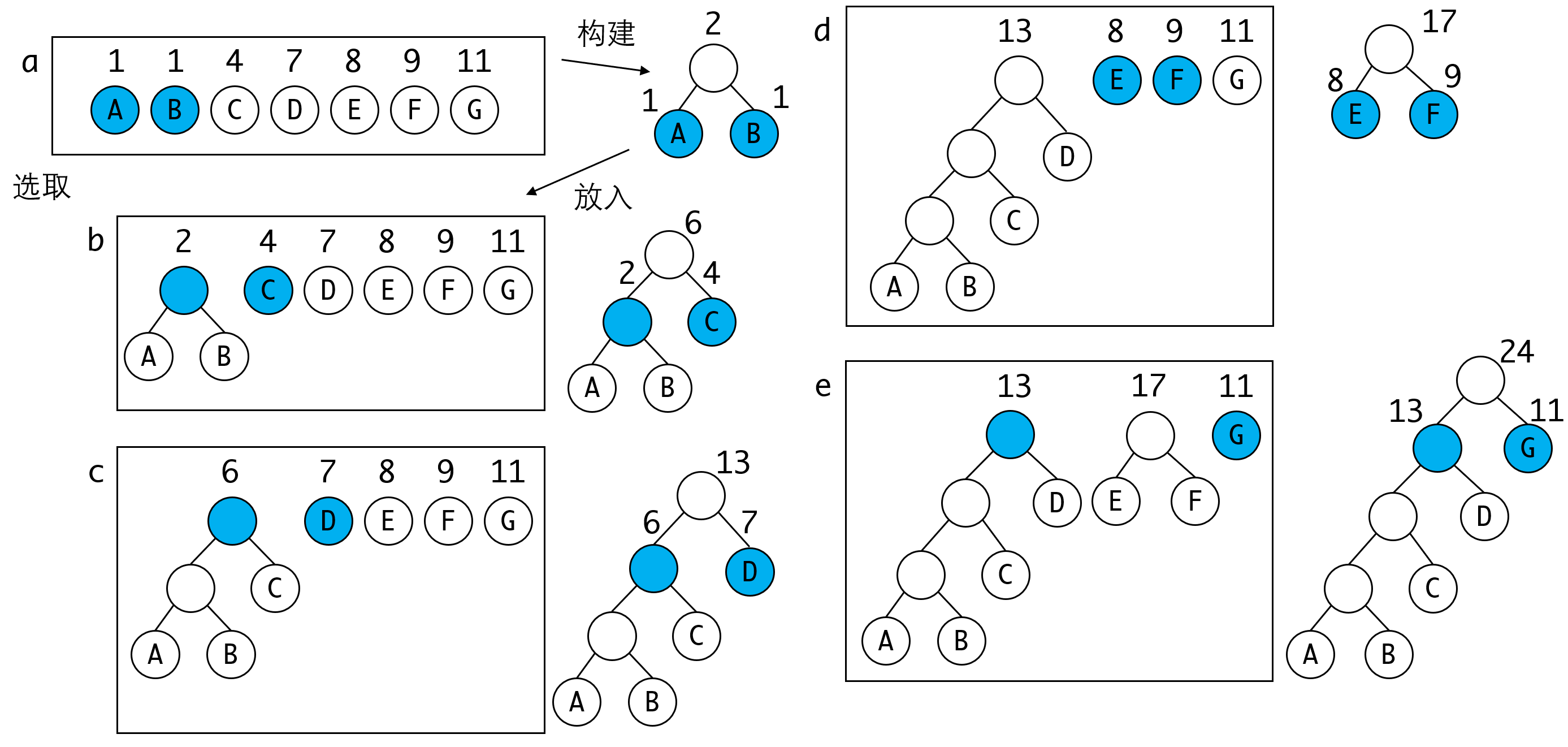
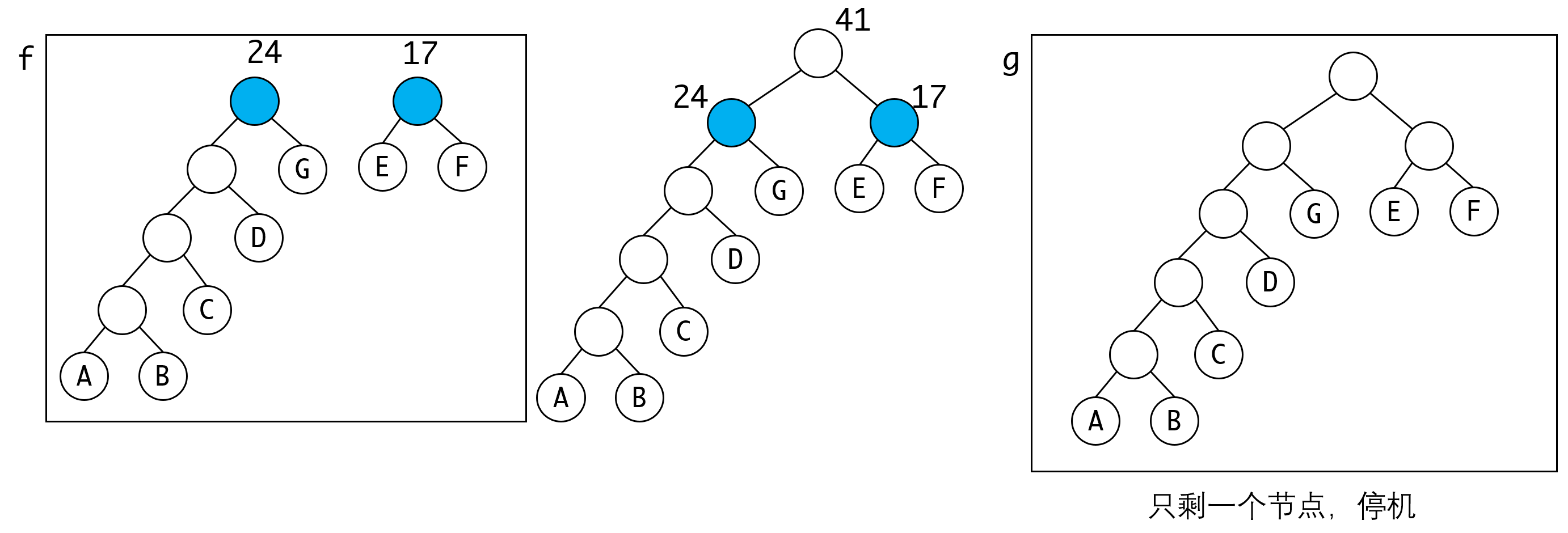
整个过程还是很容易理解的，每一回合都取出两个最小的节点，构建一棵新树并放入待选集合。重复整个过程直到只剩下一棵树为止。

那么我们有一个问题，哈夫曼树唯一吗？其实即便在我们上面的例子中，他也不是唯一的，因为两个节点都可以选择放在左子树或者右子树，我们称这种树为同构树。

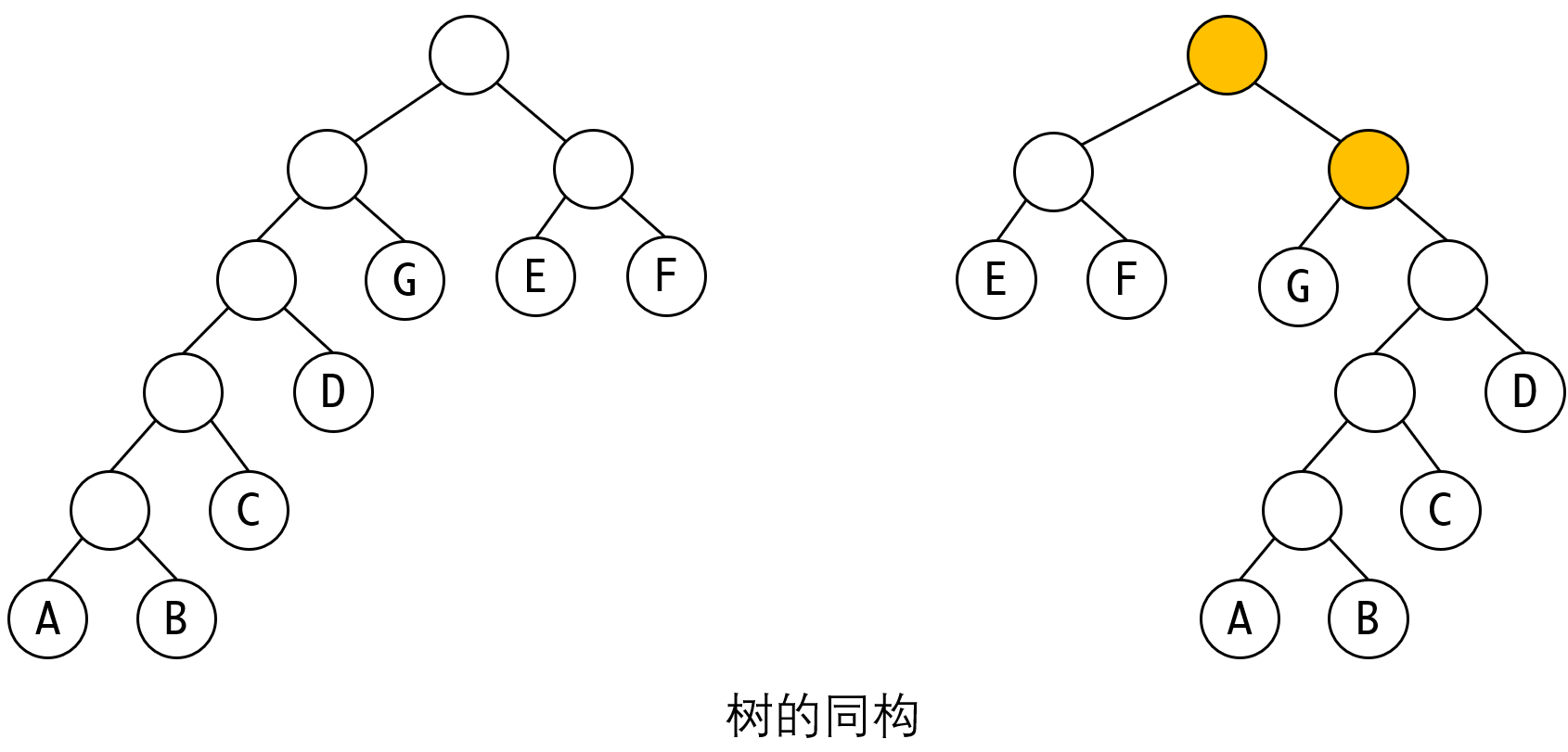
上图中，黄色的两个节点的左右子树和左侧树对应的节点正好相反（镜像），他们都可以通过上面的生成算法生成，只在相关节点选择时，将左右子树交换位置即可。

如果排除同构的情况，哈夫曼树唯一吗？我们看下面的例子：

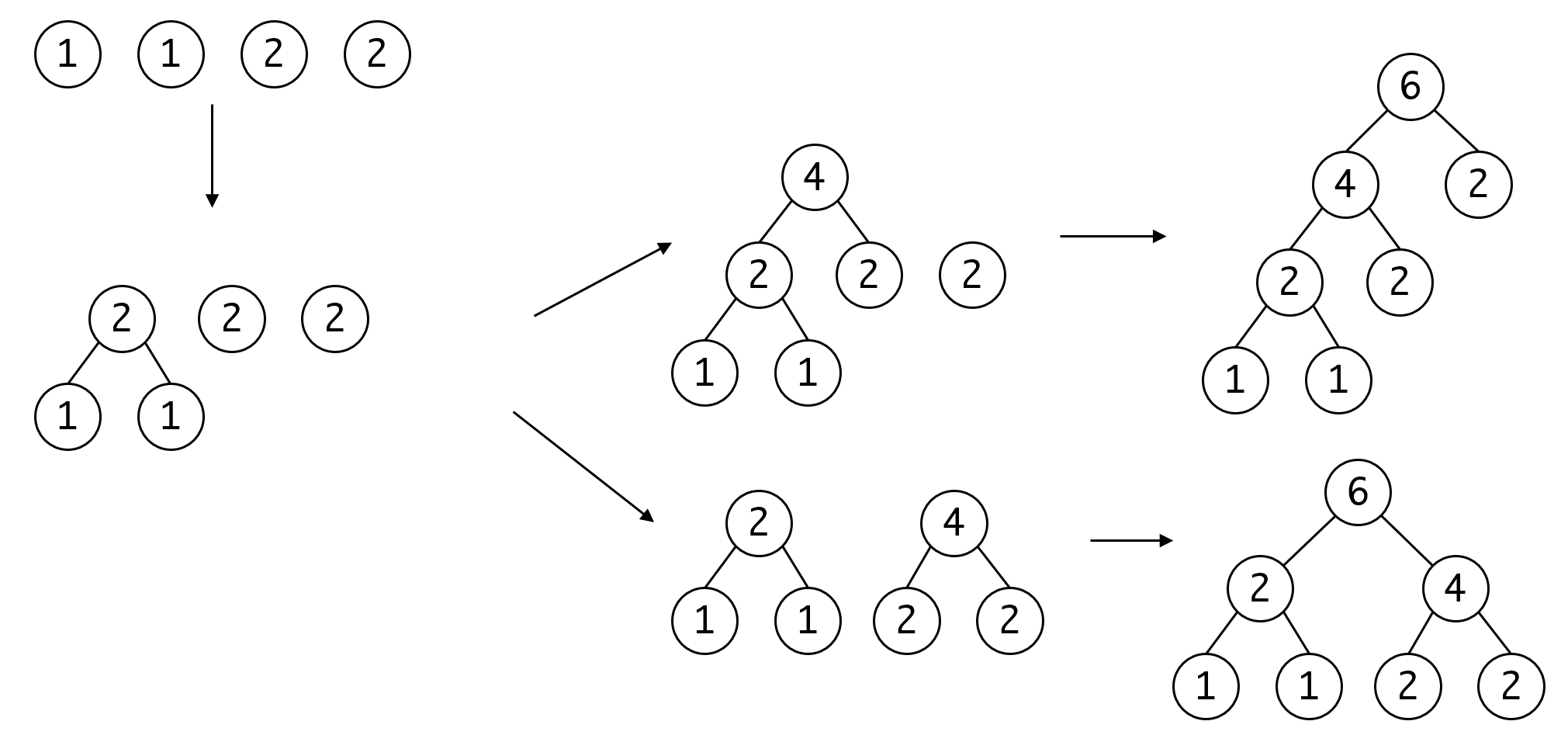
可以看到，在第二步时，我们有3个相同数值的节点可以选择，根据我们选择的不同，最后生成的树的结构也不同。那么这跟“最优”矛盾吗？

实际上并不矛盾，因为这两棵树有相同的带权路径长度，所以他们都是最优的，你可以自己计算一下。

哈夫曼树的应用——哈夫曼编码

哈夫曼树最经典的应用是哈夫曼编码。在介绍哈夫曼编码之前我们先要介绍下可变长度的编码。

假设我们有一篇文字需要编码，这篇文字只有ABCDE5个字符。其中A出现1次，和B出现1次，C出现2次，D出现4次，E出现9次。我们要如何编码呢？

一种比较简单的方法是用等长编码：因为有5个字符，每个字符最少需要3个bits，因此我们可以这样编码：

A : 000
B : 010
C : 011
D : 100
E : 101

这样我们可以得到整篇文章的编码长度=$(1+1+2+4+9)*3=51$

但这种编码方式的效率不够高，因为我们在每个编码上耗费了相同的空间开销。而实际上，虽然每个字符都是平等的，但有些字符注定比其他字符更平等:)。这里A只出现1次，但E出现了9次，如果我们给E分配较短的编码，那么即使A的编码长度会因此变长，他也是划算的。

但这要解决一个问题：即怎么才能将保证可以正确的解码。

举例来说，如果我们给E的编码为：0，那么剩下的其他字符都不能以0开始：

比如我们令：

E=0
D=1
A=01
B=001

当我们收到001时，这段编码解释成EED，或者AD，或者B都是可以的。你区分不出来。

因此假如有一个字符的编码是$x$，那么所有其他字符都不可以以$x$作为其前缀，我们把这种编码方式称为前缀码。

所以如下的编码是可以的：

A=10
B=001
C=110
D=1110
E=0

如下的编码则不可行：

A=00
B=001

A=10
B=101

我们来看要如何构建这个编码，我们先根据节点的权重（出现的次数）构建哈夫曼树：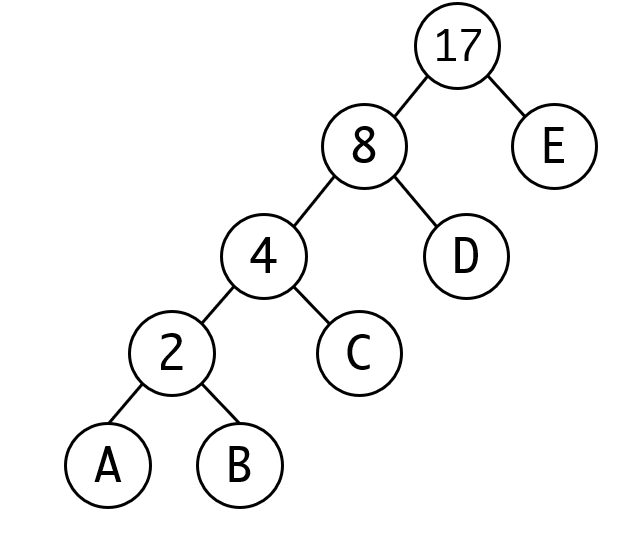

编码时，我们从根节点开始往下走，每走一层就编码一位，向左走为0，向右走为1，我们可以得到如下的编码过程：

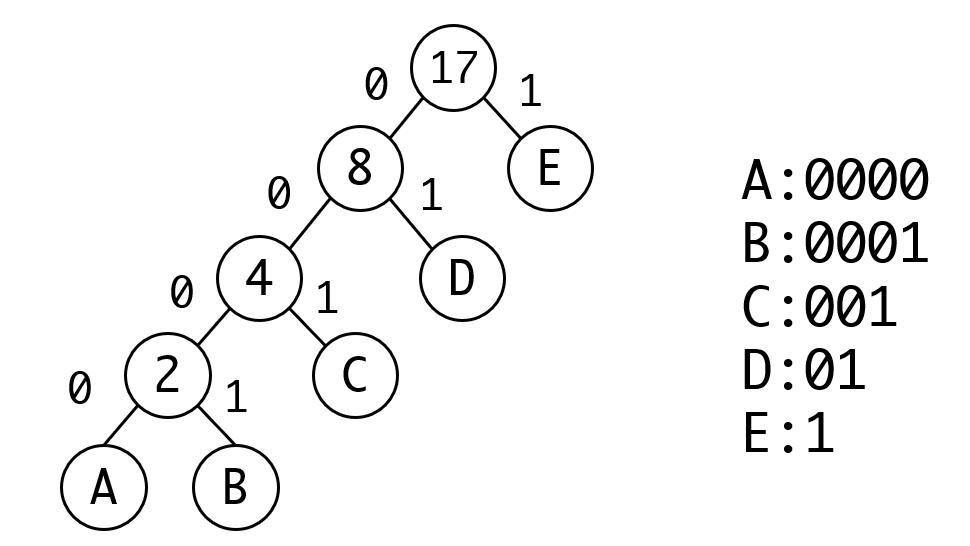
从编码的结果可以看到，没有任何一个编码是其他编码的前缀，比如假如我们收到：

0001000001

这个编码就是BAC，不会有歧义。

我们再计算下整篇文章的编码长度：

字符	出现次数	编码长度	字符占用位数
A	1	4	4
B	1	4	4
C	2	3	6
E	4	2	8
E	9	1	9

总长度等于$4+4+6+8+9 = 31$，显著低于等长编码的51。