红黑树(*)
红黑树(*)
写在前面
本节你可以不看,反正考试不考,所以我会长话短说
定义和性质
红黑树是一种相对比较复杂(如果不是最复杂)的数据结构。他也是一种(准)平衡树。
我们先看定义,再看看他跟AVL树有何区别。
红黑树是这样一颗树:
- 所有节点存在两种颜色,红色和黑色
- 根节点为黑
- 到任意叶子节点的路径上,黑色节点的数目都一致
- 红色节点不能直接相连
- 空指针也认为是黑色
- 插入任意节点时,节点总为红色,插入后再调整平衡。
这里要注意的是3和4,这两条规则决定了红黑树的平衡性。
我们假定有这样一棵树:
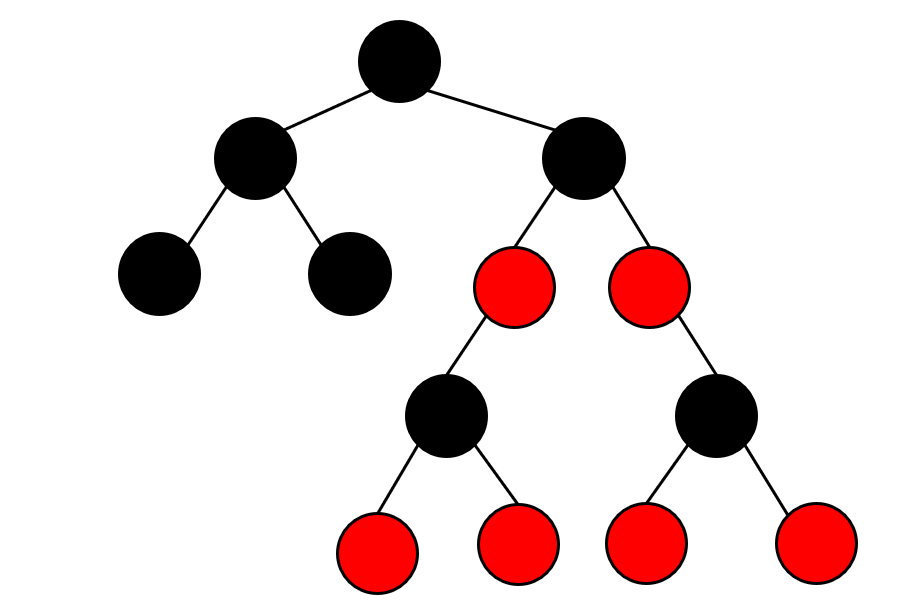
我故意让右侧第一层红色节点只接一个子树,方便观察,实际上他们都可以再接一组子树。
如果我们去掉红色节点,我们就得到了一棵满二叉树,也就是最完美的平衡状态。这就是为什么有3的原因,每条路径上黑色节点数目保持一致,保证最优的搜索效率。 但显然满二叉树是无法表示任意数目的节点的,就像你手里只有10块,100块,1000块的整钱,要凑出任意数目的钱数,你还需要零钱。而这里零钱就由红色节点来负责。这就是为什么需要两种颜色的原因。
但你不能滥用零钱,我们需要保证在能使用整钱的情况下要尽可能的使用整钱,否则规定3就失去了意义。所以对零钱的使用就有了4这个限制。他保证最坏的情况下左右子树的高度差也不会超过2倍。就如同上面的例子,左子树有2层,右子树有4层。两者正好相差一倍,此时你已经无法在右子树上再增加任何一层了:
- 如果你增加红色,那么必然两个红色节点会相连
- 如果你增加黑色,那么有一条路径上的黑色节点数目会超过其他路径
理解了红黑树的这个本质,我们可以看出他跟AVL树的不同
- 红黑树的平衡性不如AVL——所以他的搜索效率要低于AVL
- 红黑树对平衡的容忍度比AVL高——也就意味着他所需要的调整操作比AVL少(更稳定)
我们以查找效率为代价,获得了一种需要更少调整的数据结构。实际上现实中的大多数树形容器都用红黑树来实现,他的稳定性是非常吸引人的一种性质。
处理过程全貌
红黑树处理的复杂度远远超过AVL树,我们需要对所涉及的操作先有个大概的了解:
插入
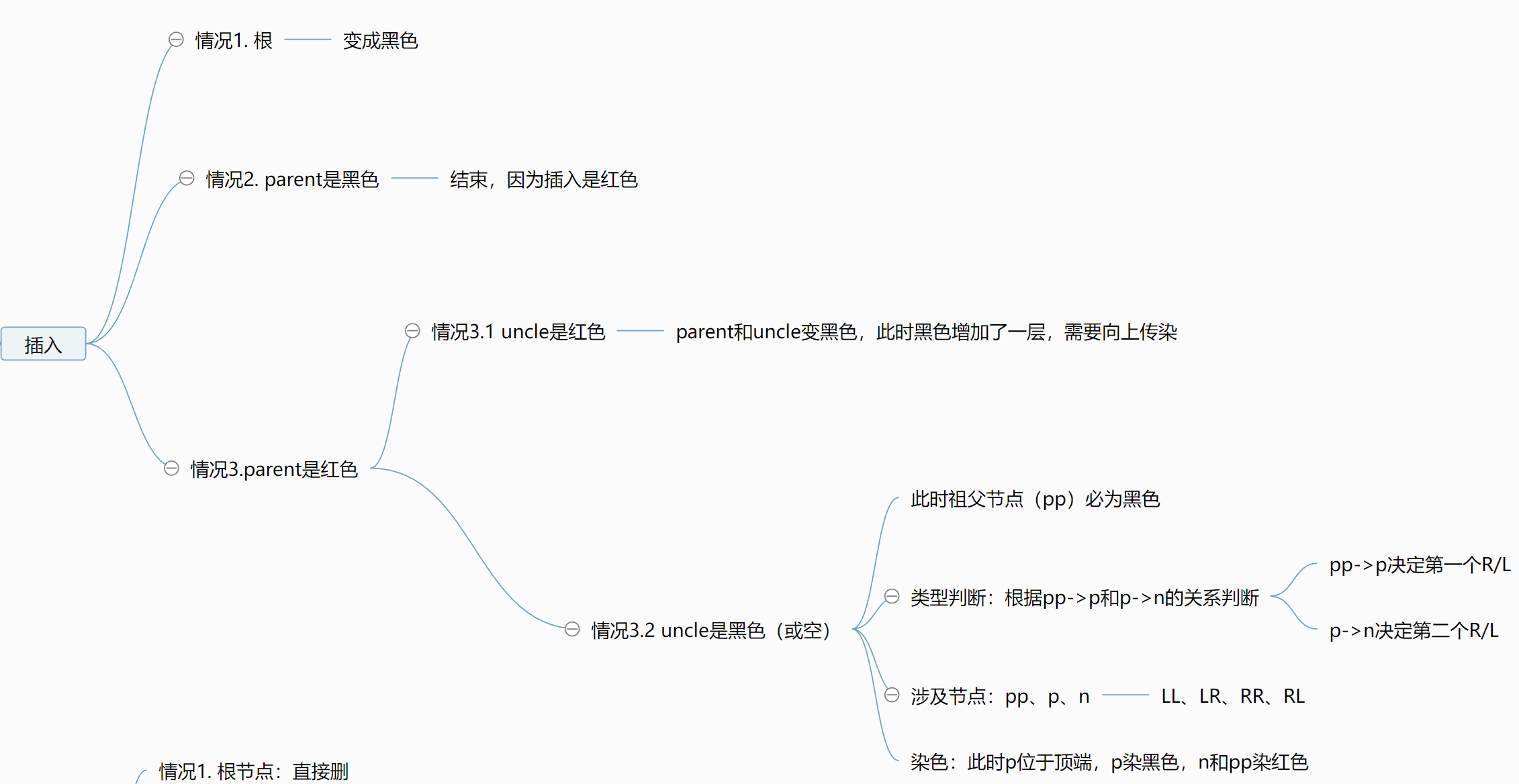
看到这个图相信大家已经感受到红黑树深深的恶意了。别着急,还有删除。
删除
如果说AVL树的操作是Monkey级,那红黑树的插入是困难级,而红黑树的删除就是地狱级。
看图:
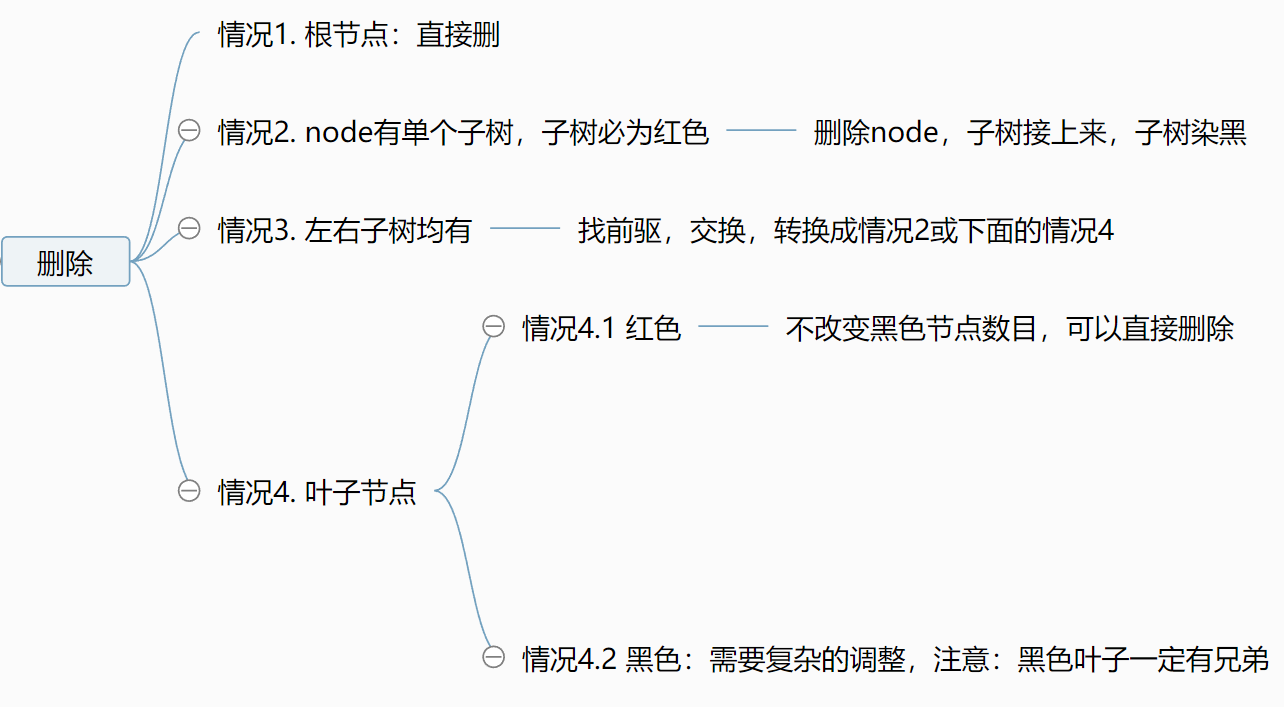
也就这样嘛,你觉得智商受到了侮辱,别着急,没看4.2我没展开吗?

希望这三张图能让你对红黑树的复杂度有一点点了解。

不过实际上不用过分担心,红黑树的处理逻辑确实非常复杂,但没有无法理解的内容。 删除的复杂度在于要保证黑色节点数目的平衡。所以你可以看到上面的处理流程中向父亲、兄弟、兄弟的孩子节点(侄子)到处借红色的节点,然后变成黑色。
最后实在借不了,只能向上向祖父,曾祖父,曾曾祖父……去接,借到最后回到根节点,问题一定可以解决。
只要你前期的代码规划的足够好,也就是拿着指南一步步写的事。千万不要相信徒手写红黑树的谣言,这是超越人类能力的事。我们一般管这种人叫畜生。
是否需要用B树去理解红黑树?
你可能听说过红黑树本质上是2-3-4树,也就是4阶B树。那么有必要从更高维度去理解他吗?我个人觉得没有必要,因为红黑树处理的逻辑是非常清晰的,就是围绕黑色节点的数目来做文章。用B树去理解他反而是多此一举。
实际上算法导论和算法这两本书里,也是直接上红黑树的。
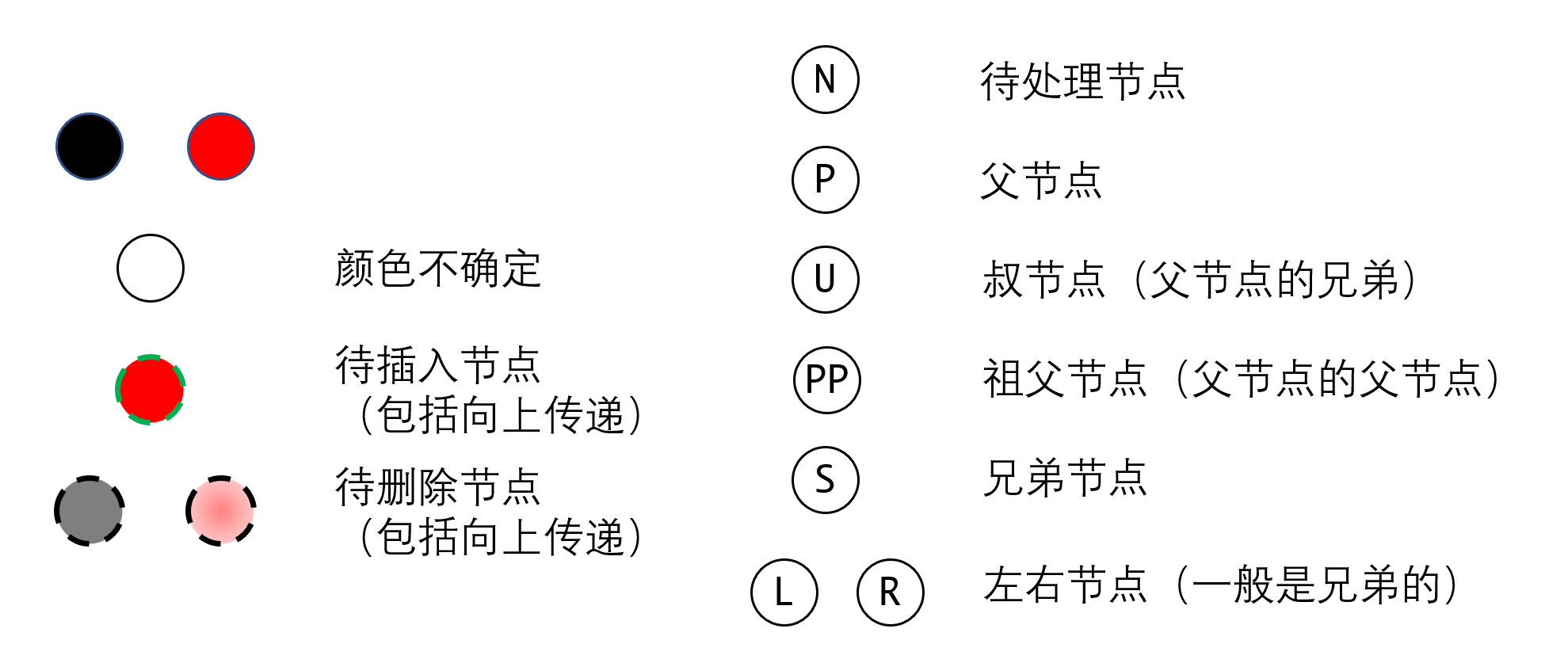
图例约定
红黑树的操作非常复杂,远远超过AVL,涉及的节点也非常多,我们先做如下约定:
插入
插入的第1、2种情况比较简单,根节点按要求直接变色。而父节点是黑色节点的情况,插入红色节点也不影响平衡性

第三种情况要分情况讨论:
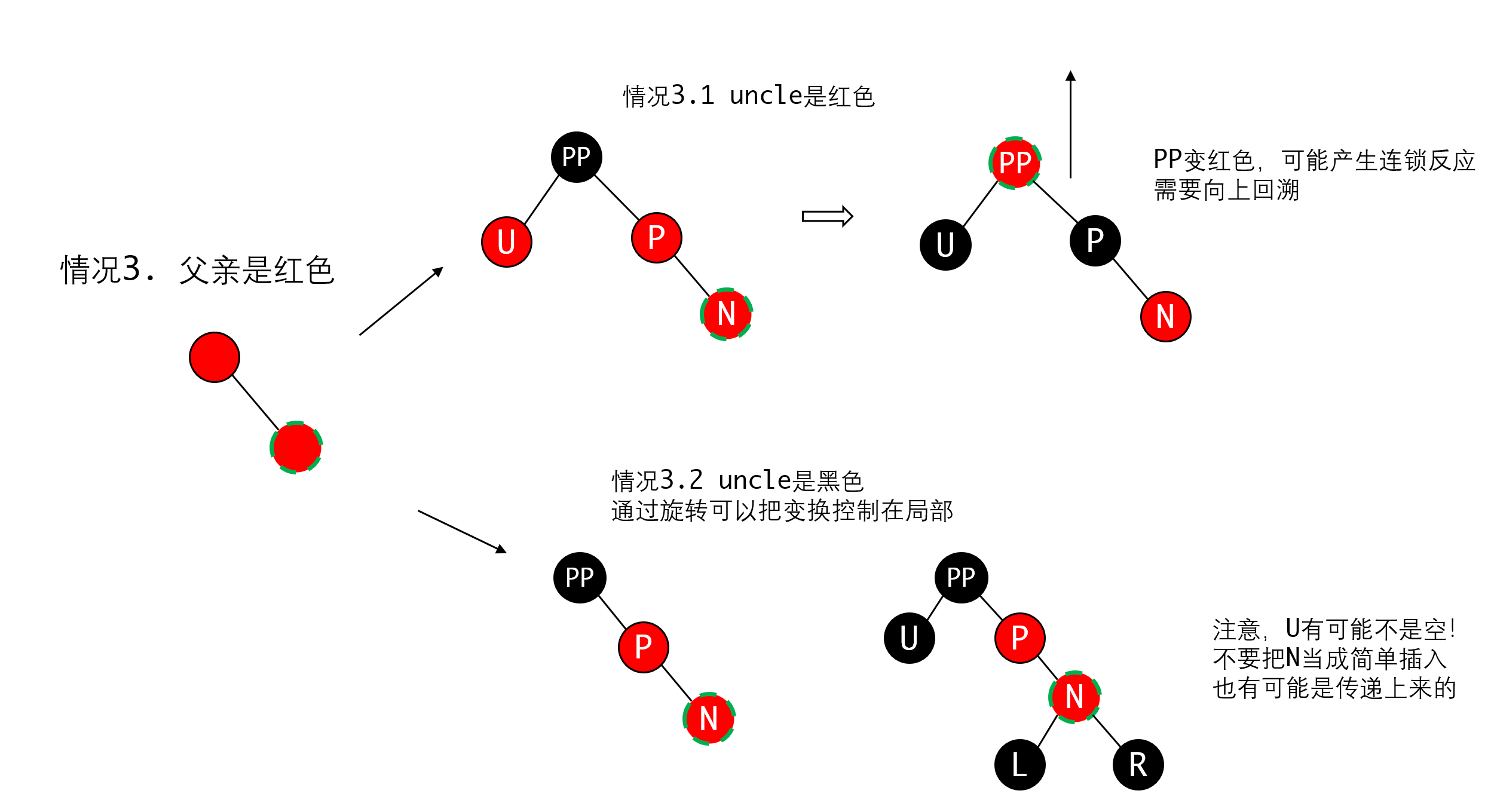
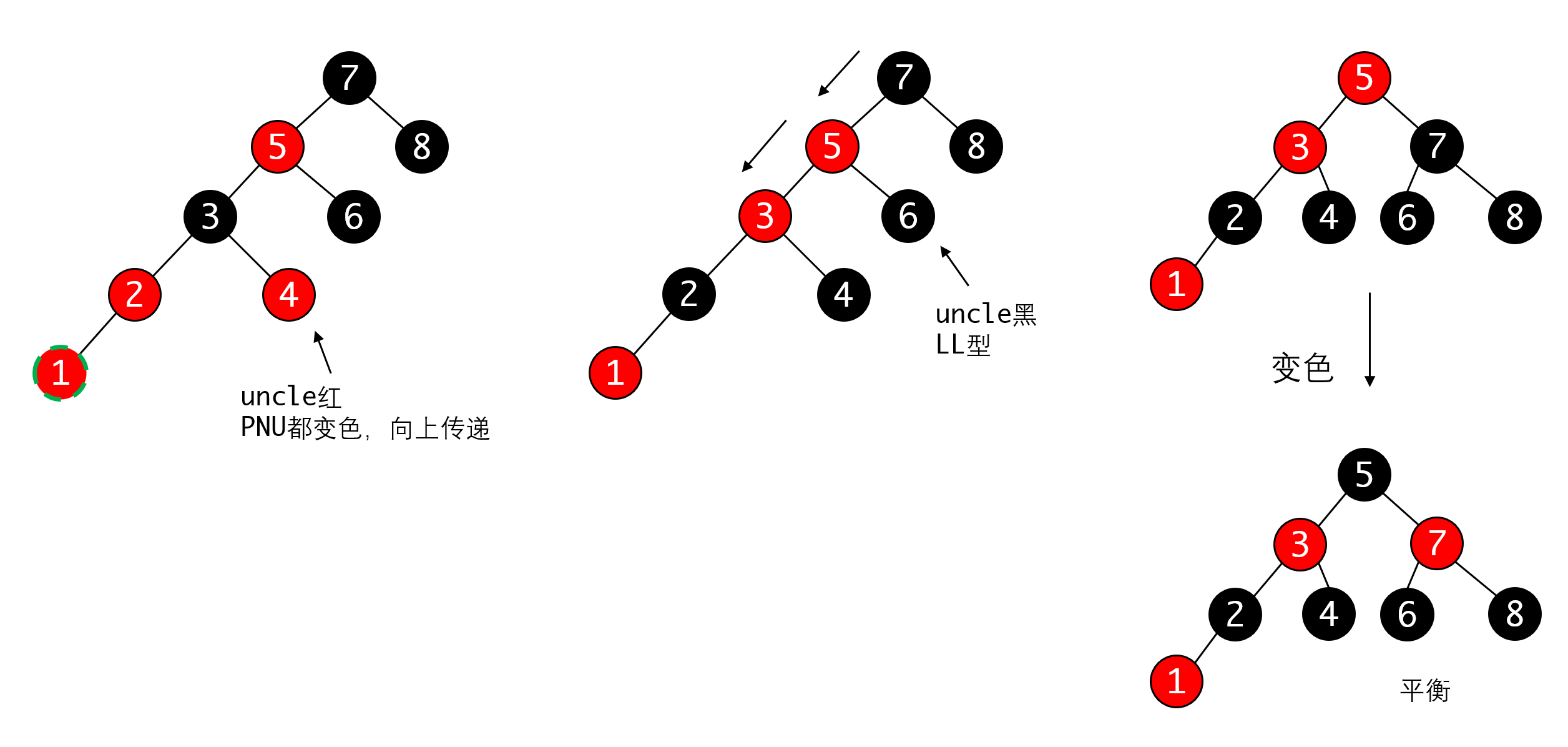
如果父亲的兄弟(uncle)也是红色,我们可以把他们都变成黑色,这样保持两条路径上的黑色节点还是一致的,但这样我们就需要把PP变成红色,才能保证这个子树上的黑色没有变多。此时因为我们不知道PP的父节点的颜色,所以需要向上回溯(即把PP当作插入节点向上继续操作)。
如果叔节点是黑色的,那么我们可以通过旋转把变换控制在局部
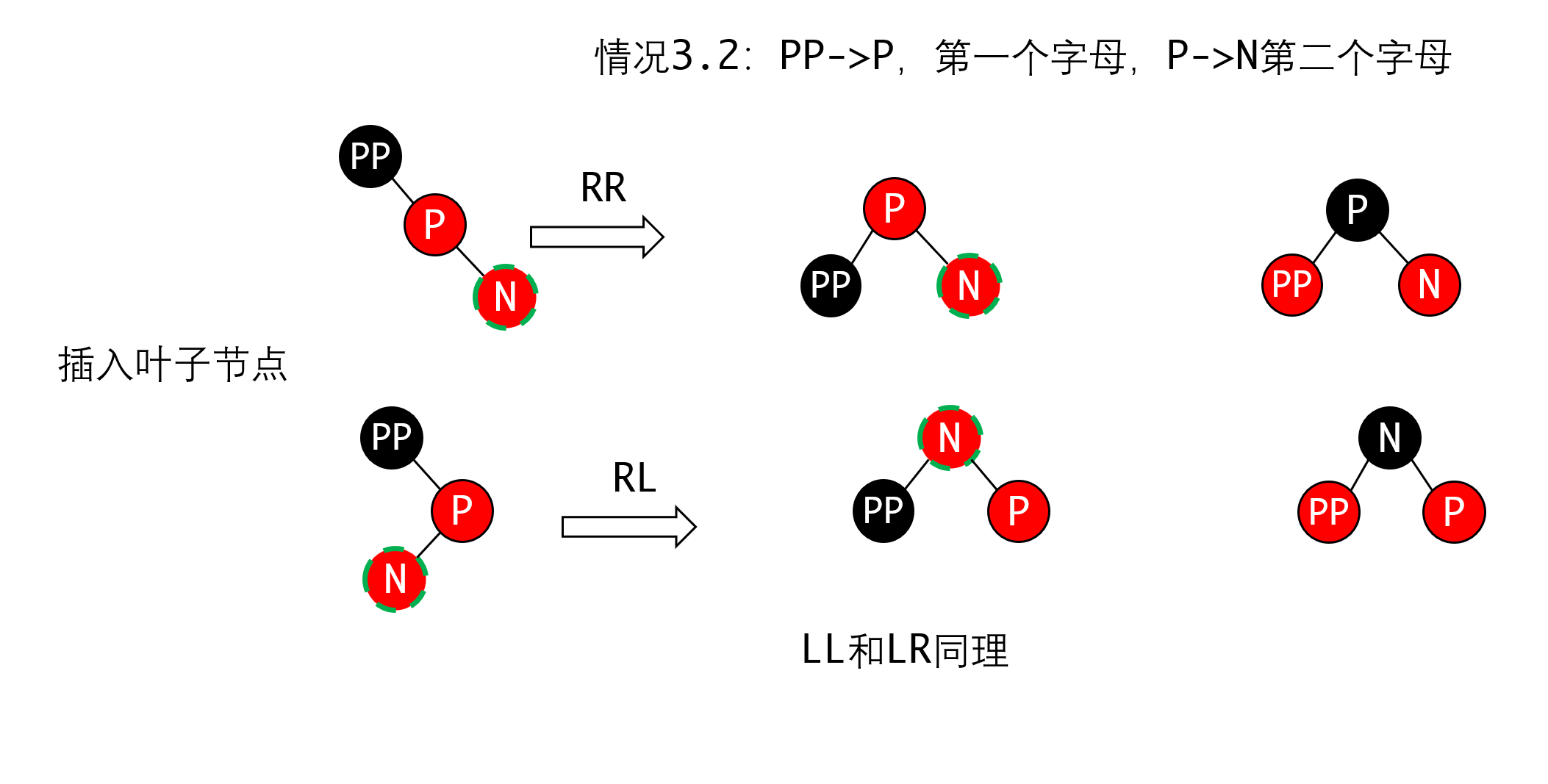

这里要注意有两种可能,一种是插入时,父节点是红色的,此时叔节点U不可能存在,但我们把空指针也看做黑节点,可以用相同的逻辑处理。
另一种是叔节点U存在,这种情况说明N下面一定还有黑节点,否则不可能平衡。那么N一定是从下面传递上来的红色节点。
插入的逻辑到此为止了。可以看出整个逻辑还是很清晰的,能把变色局限在局部,我们就局限在局部,实在不行了,再向上传递。
删除
删除就要复杂很多了,我们还是看最简单的几种可能:
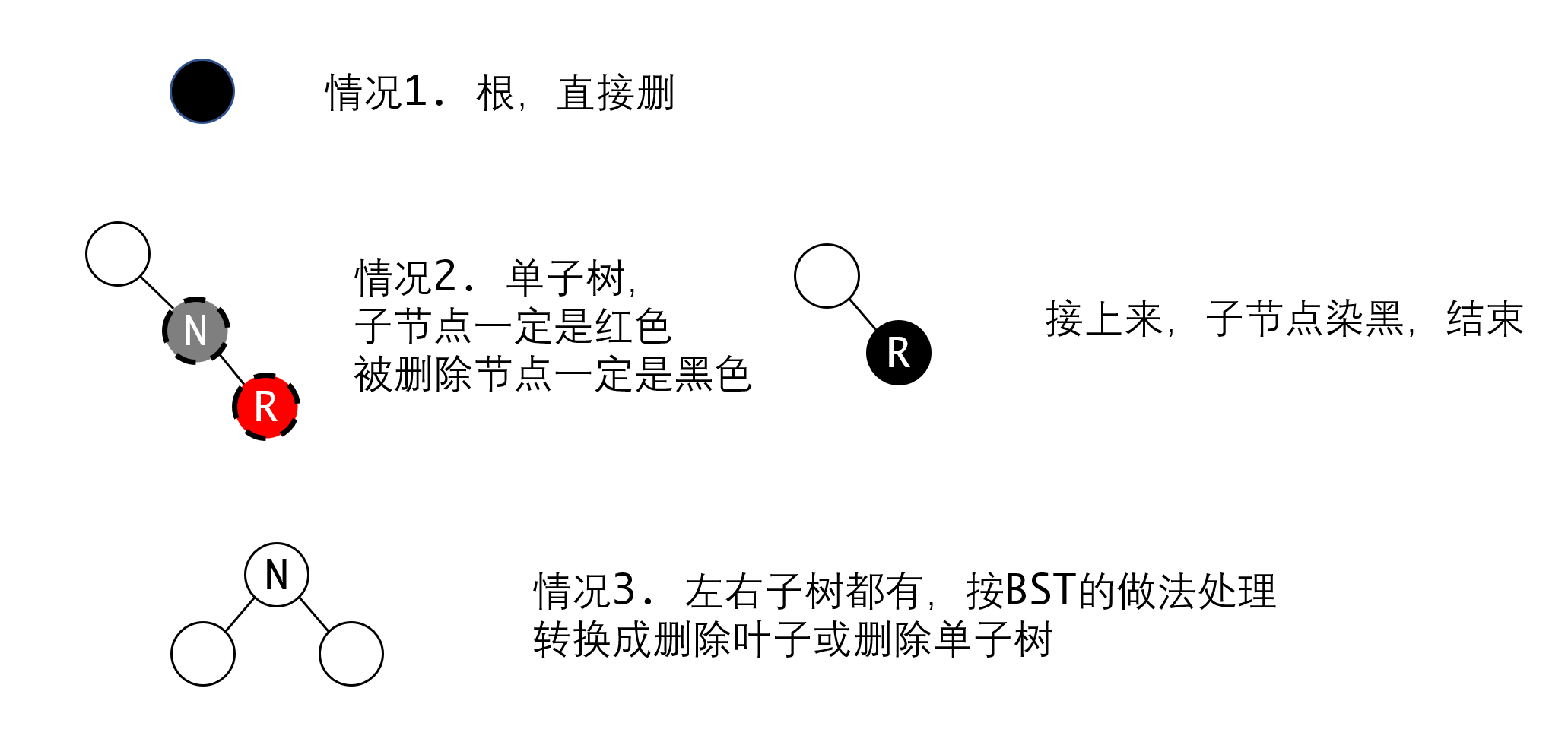
这三种情况都很好理解,第二种情况下,接上来之后整条路径的黑色也没有发生变化。
情况3则依据BST的做法,转换成情况2,或者下面的情况4。
接下来是删除叶子节点的情况:
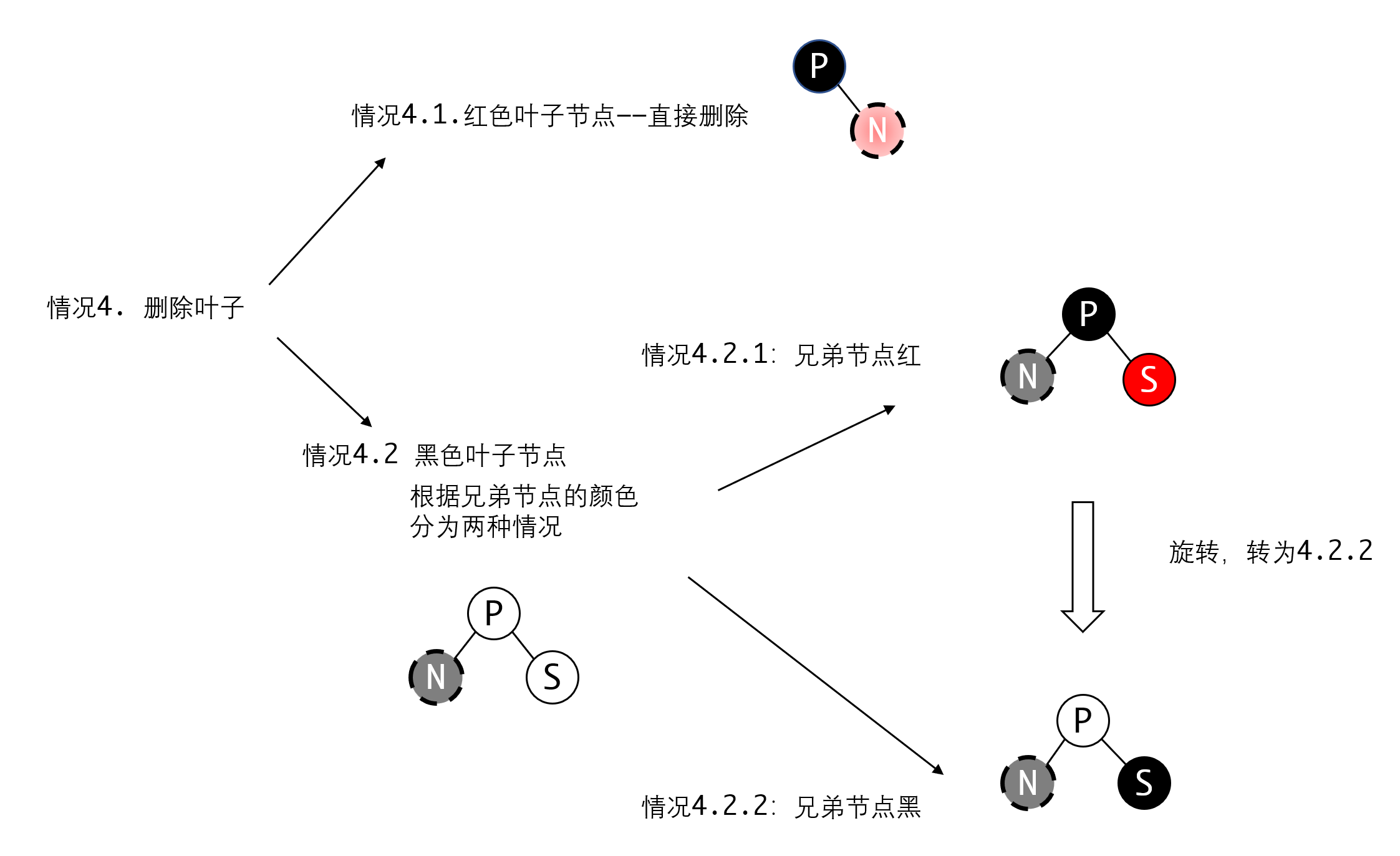
红色叶子非常简单,直接删除即可。不影响平衡。
黑色叶子则是整个红黑树里最复杂的部分。但最终会转化为4.2.2这种形式,也就是兄弟节点也是黑色的,然后执行删除。这样在这个局部是暂时平衡的,才能方便我们调整。
对于4.2.1这种情况,我们可以通过旋转,让N和S变成同一种颜色再处理,也就是转化为4.2.2来进行处理:
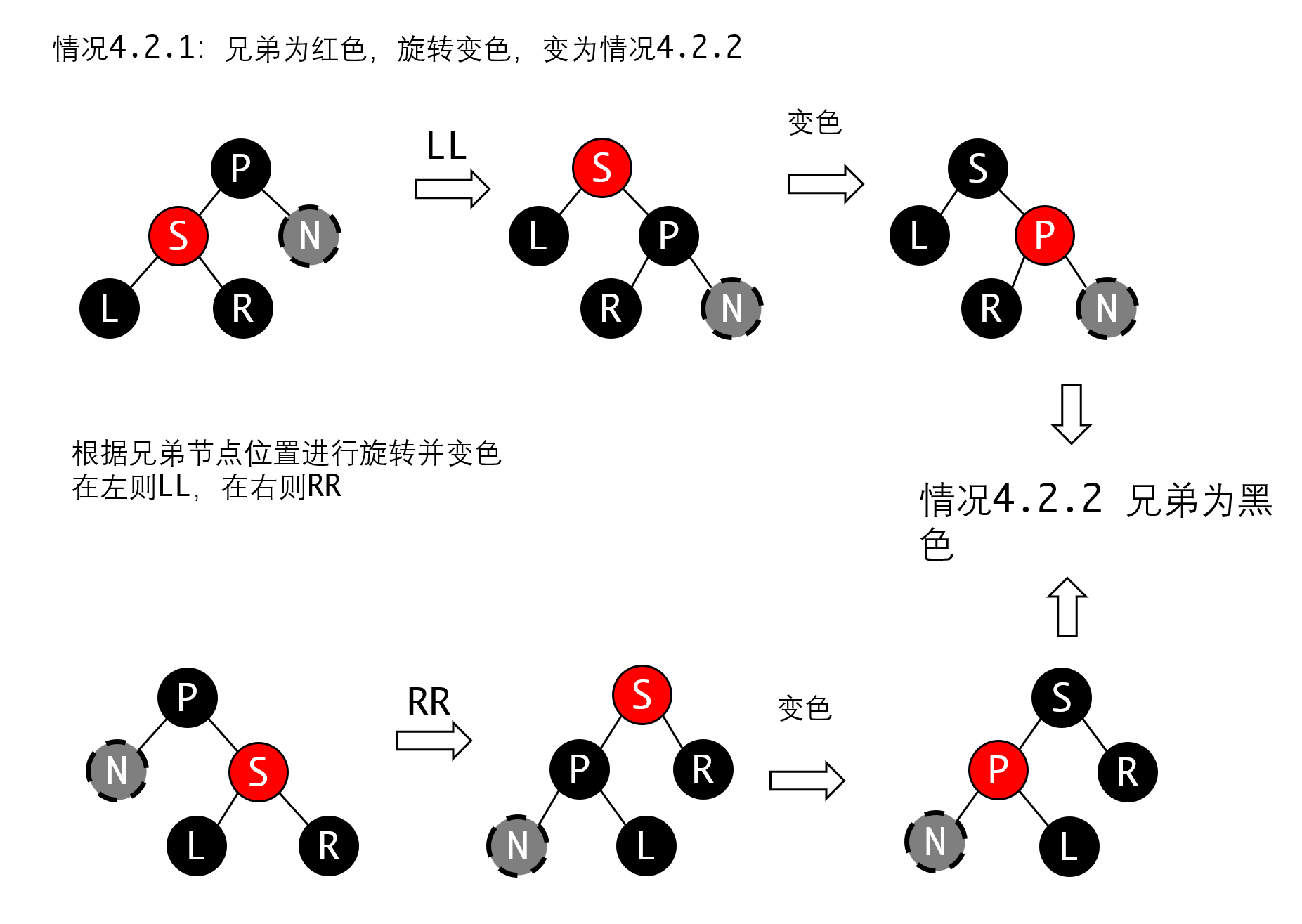
最终都会转化为父节点是红色,两兄弟都是黑色的情况。
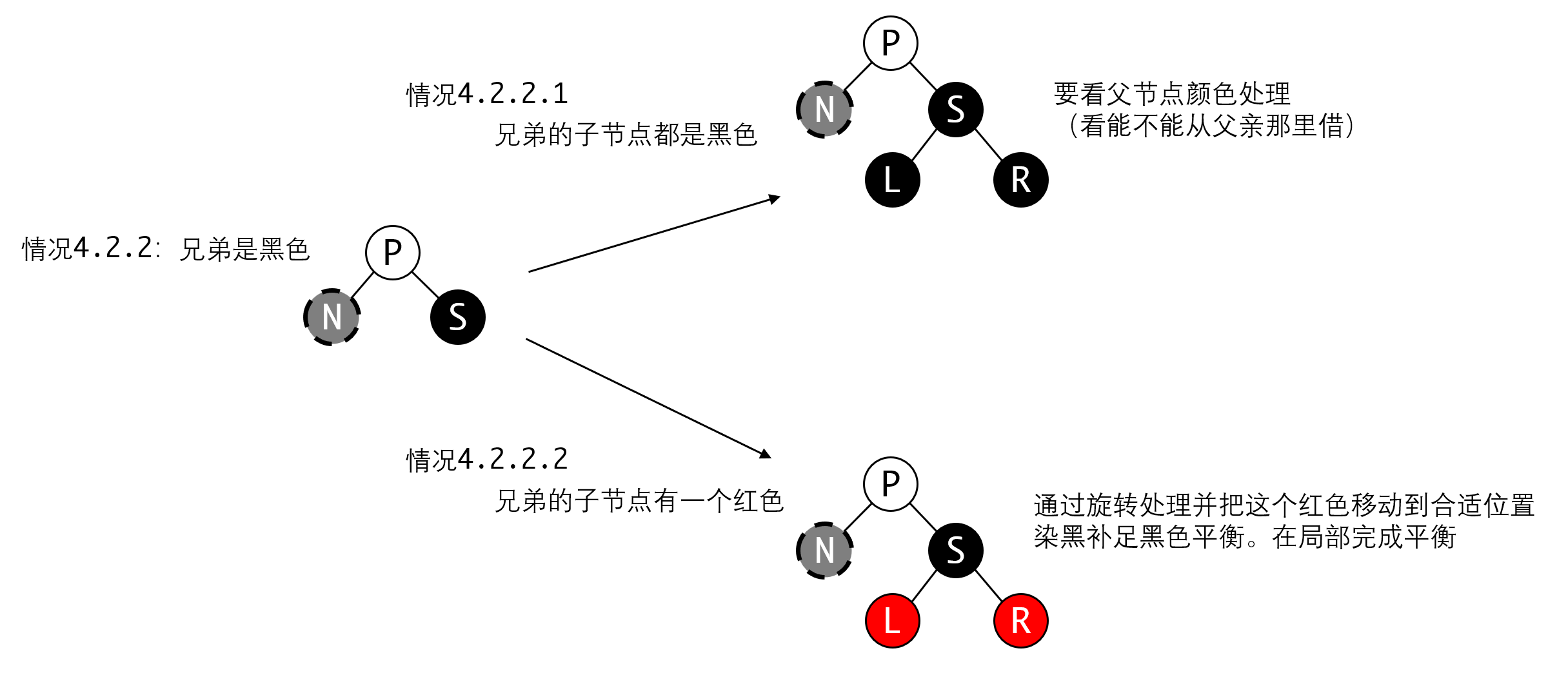
所以我们只需要处理兄弟节点也是黑色的删除情况(4.2.2),根据兄弟节点的子节点(也就是待删除节点的侄节点)的颜色有不同的处理。
如果侄节点没有红色节点(4.2.2.1),那么我们就要看父节点有没有红色可以借来染色,补足局部的黑色。
反之如果侄节点有红色节点存在(4.2.2.2),我们可以通过旋转把这个节点移动到合适的位置,染成黑色,补足这个局部的黑色,使其重新达到平衡。这样我们就把变换局限在局部,不需要向上传递了。
如果侄节点没有红色节点而且父节点也不是红色的,那就只能向上传递。
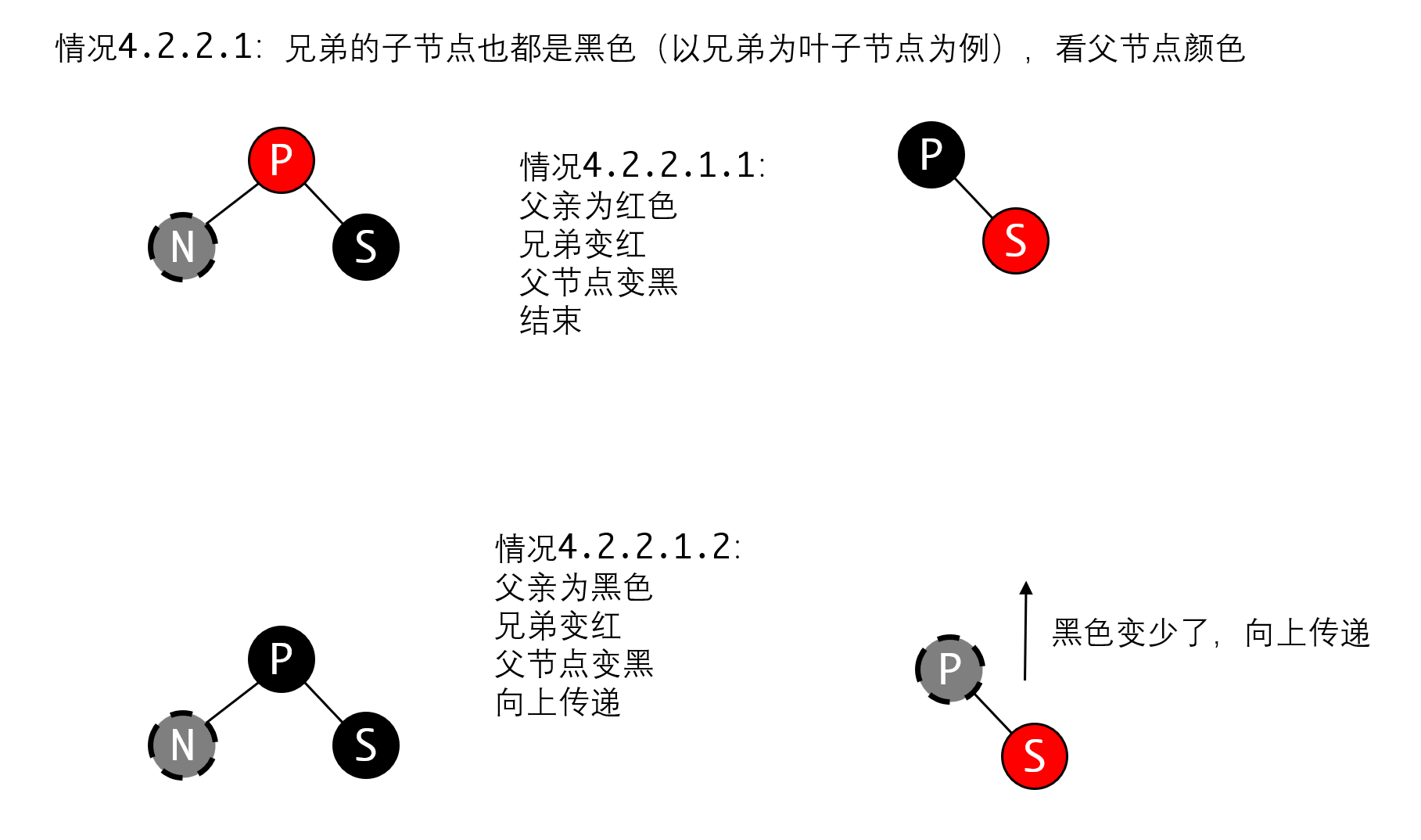
4.2.2.1 我们可以分两种情况讨论,但他们的处理方式都是一样的,从这里也可以看出为什么要把空节点也视作黑色,第一种是待删除的节点是叶子节点,那么兄弟节点必为黑色(为什么?)。
我们此时如果父节点是红色,那么很好,我们将父节点变为红色,兄弟节点变为黑色,这个局部重新平衡,且黑色节点数目没有变化,直接停止即可。
如果父节点是黑色,就没有地方可以借一个红色过来处理,那么此时我们只能把这种情况向上传递了。所以我们把兄弟节点S变为红色,保持局部平衡,然后向上传递。此时相当于这个分支的黑色少了一层,需要上面的层次来帮我们平衡。
另一种情况是N是下层处理后无法平衡向上传递的产物,我们再看从下层传递上来的情况:
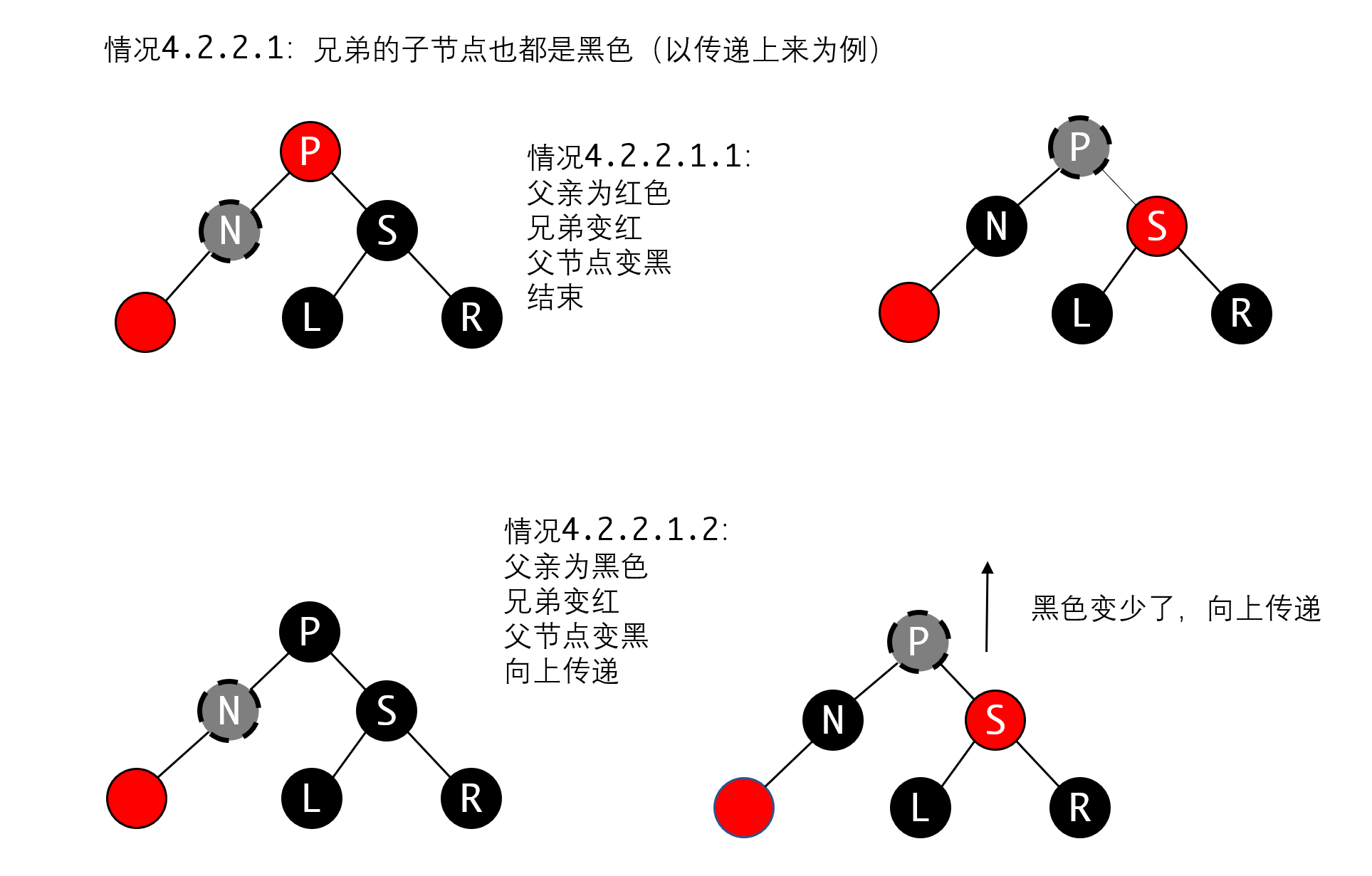
当N是从下方传递上来时,就说明N这侧的黑节点层次比另一边要少一层,类似上图的形式。处理过程也是一样的,分两种情况处理即可。
4.2.2.2 也可以分为两种情况讨论,他们的处理方式也是一样的,这里区分出来是为了更深入地理解处理的整体逻辑:

到此为止我们就将红黑树删除的所有情况都都讨论完毕了,其实逻辑并不复杂——能找父节点、侄子节点借用,就拿过来在局部平衡,不行就向上传递。只是分类的情况比较多,导致看起来逻辑很复杂罢了。
练习
我们看两个练习巩固一下学习的成果:
插入元素

点击查看答案
删除元素
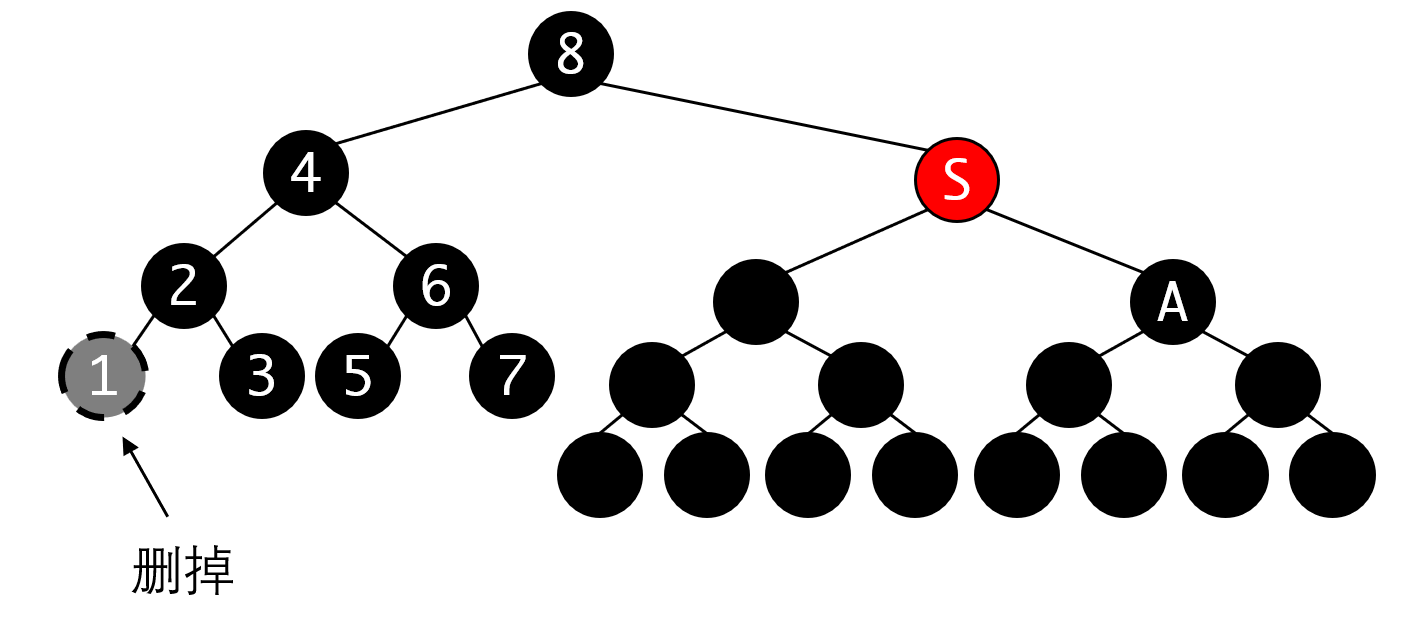
点击查看答案
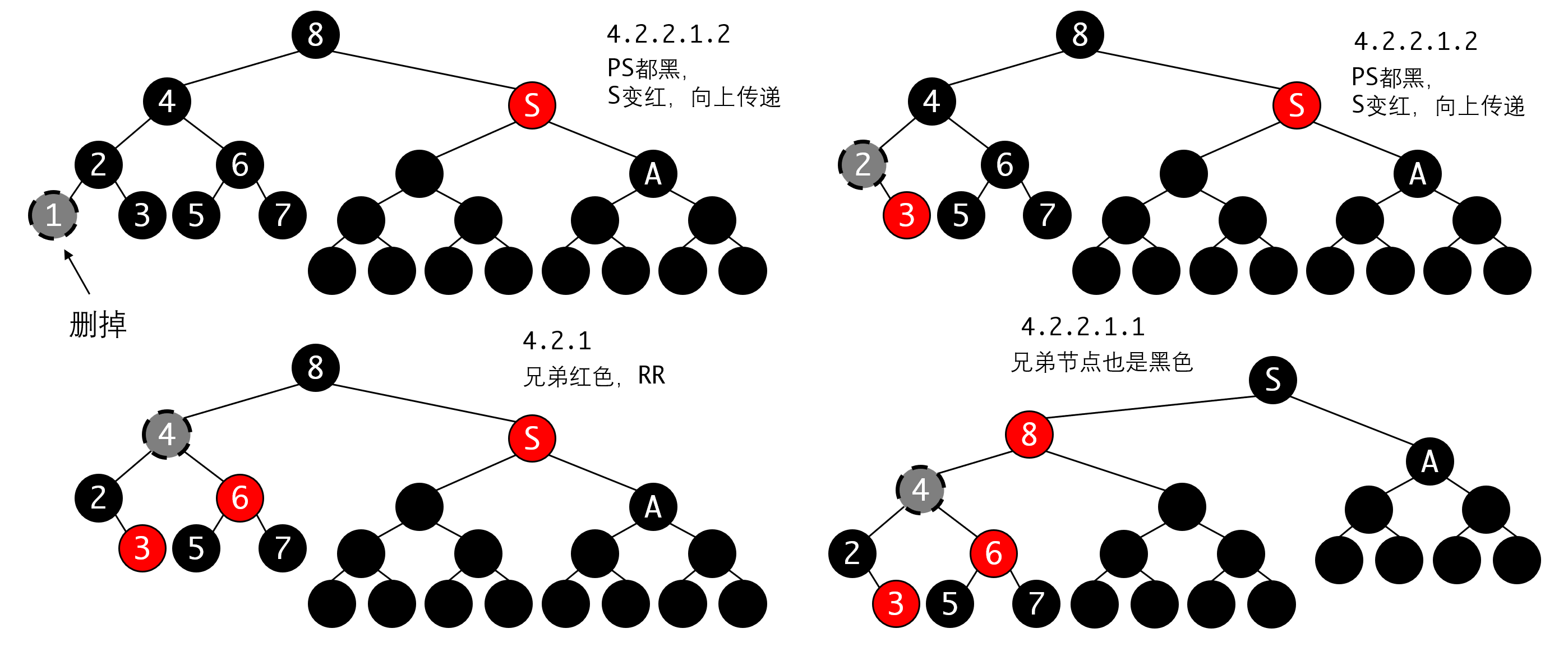
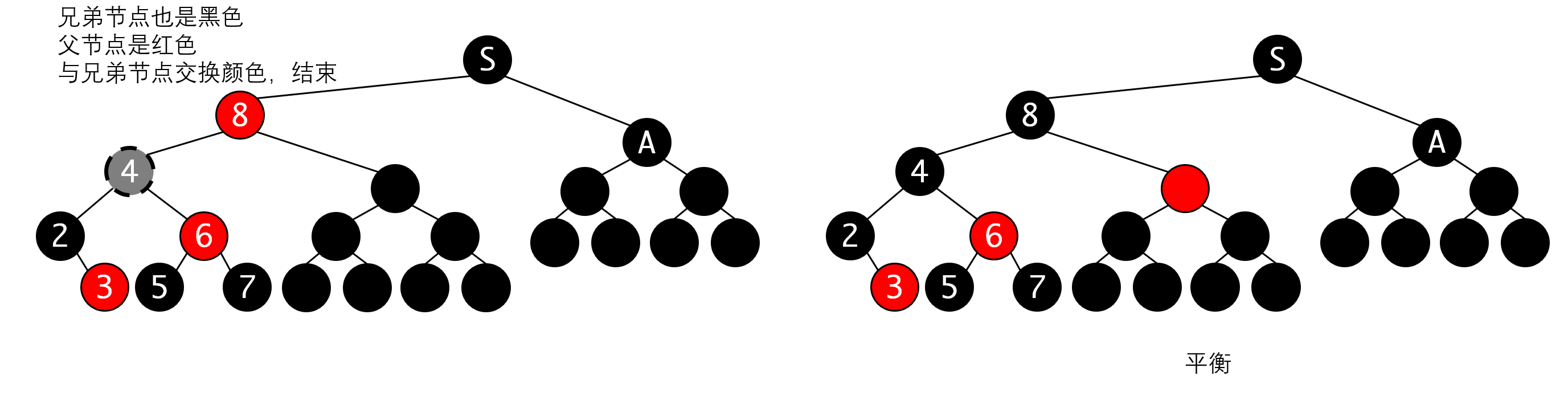
从这个例子可以看出所谓的稳定性从何而来。在向上回溯的过程中,只要父节点、兄弟节点或者兄弟节点的子节点(侄节点)有任何一个节点是红色,那么整个上溯过程就可以停止了。