优先队列和堆
优先队列和堆
优先队列
回顾下前面哈夫曼树的构建过程,我们每次都需要取出其中权重最小的两个节点。这是一个在很多算法中都需要的操作。比如后面的图的最短路径算法、或者最小生成树算法等等。
实现这一要求的数据结构叫优先队列,注意优先队列和后面要讲的排序树是有很大不同的,排序树里,数据是可以有序访问并且有序查找的。 但优先队列我们只要求能取出最大或者最小的那个元素即可,其他元素则没有要求。
我们知道在一个线性表中获取最大值的算法复杂度是。 而如果希望这个过程能尽量快点,你可能会希望能对线性表的内容进行排序。 但这样处理的问题是:向一个有序的序列里插入元素,要保证结果有序,你可能会需要的复杂度。的复杂度就不如直接使用线性表了。
因此我们需要一种能够降低放入、取出效率比高的数据结构,这种数据结构就是堆。
堆
堆实际上是一个用顺序存储的方式来存储的完全二叉树。如果你已经忘记了相关的概念,请回去阅读本章第一节中二叉树的顺序实现这一部分。
定义:如果一棵完全二叉树的根节点比左右节点都大,并且所有子树都满足这一条件。我们称他是一个大顶堆。反之,如果根节点比左右节点都小,并且所有子树都满足这一条件,我们称他是小顶堆。
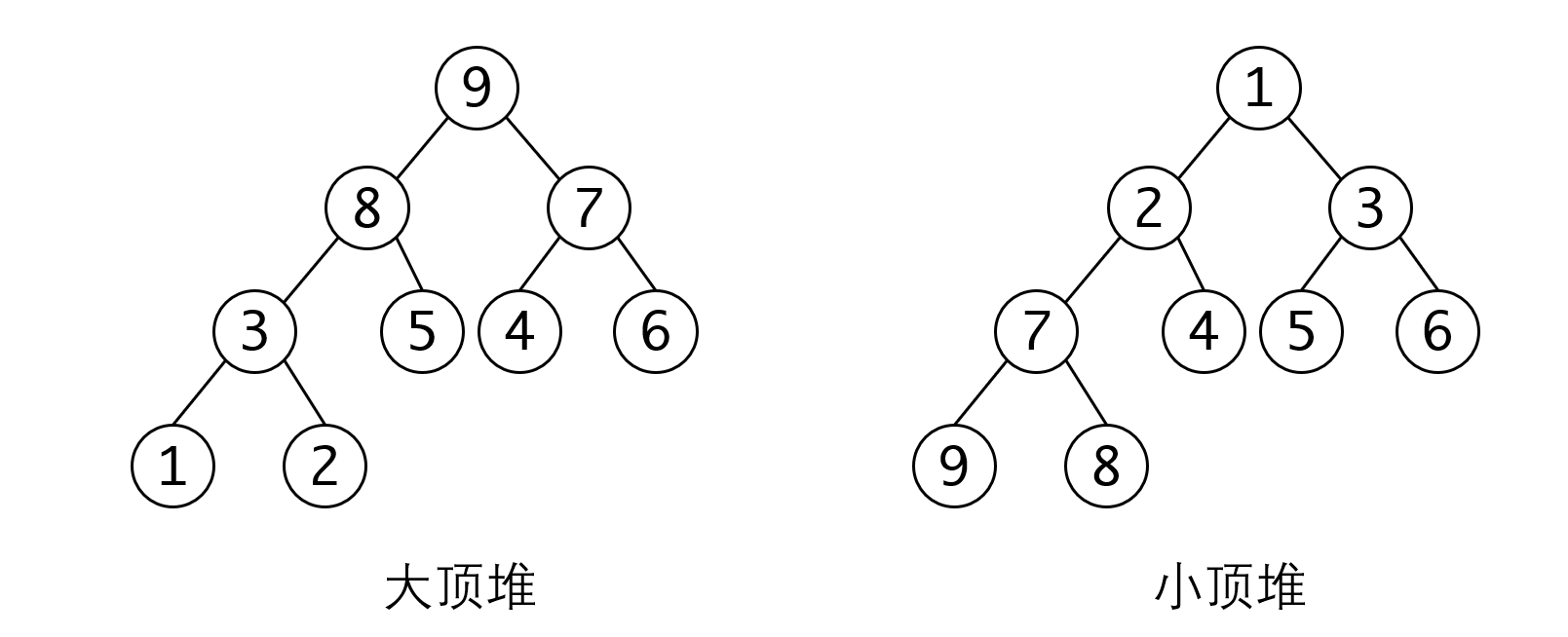
很显然,堆也是一个递归定义,而且根据这个递归定义我们可以推断出,最小(最大)的元素一定是小顶(大顶)堆的根节点,这使我们可以很方便地获得元素的最小值和最大值。
为了简化讨论,以下讨论的堆都以小顶堆来讨论。
注意你可能会认为堆的每一层都会比上一层大,实际上并非如此,你可以说左右子树都的元素都一定比根节点小。但不能推出每一层属于不同子树的节点也有类似的性质:
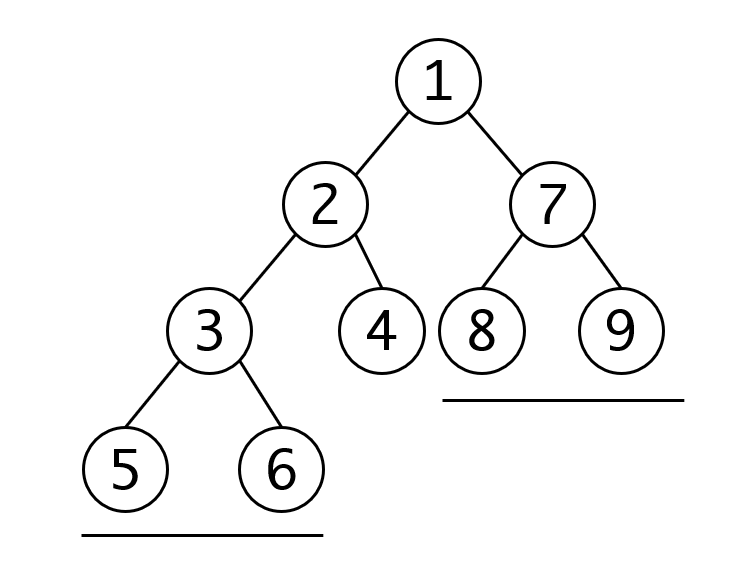
第三层的8、9两个节点就比第四层的的5、6两个节点大,但这个二叉树依旧符合堆的定义,即根节点是所在子树的最小值。希望通过这个例子能让你对堆有一些感性认识。
堆的表示
前面已经介绍过,我们用顺序表(数组)来表示完全二叉树。对于堆,一般我们会用一个非常小的元素来占用下标是0的位置,这个元素称为守卫,我们可以在下面堆的插入和删除中看到他的作用。
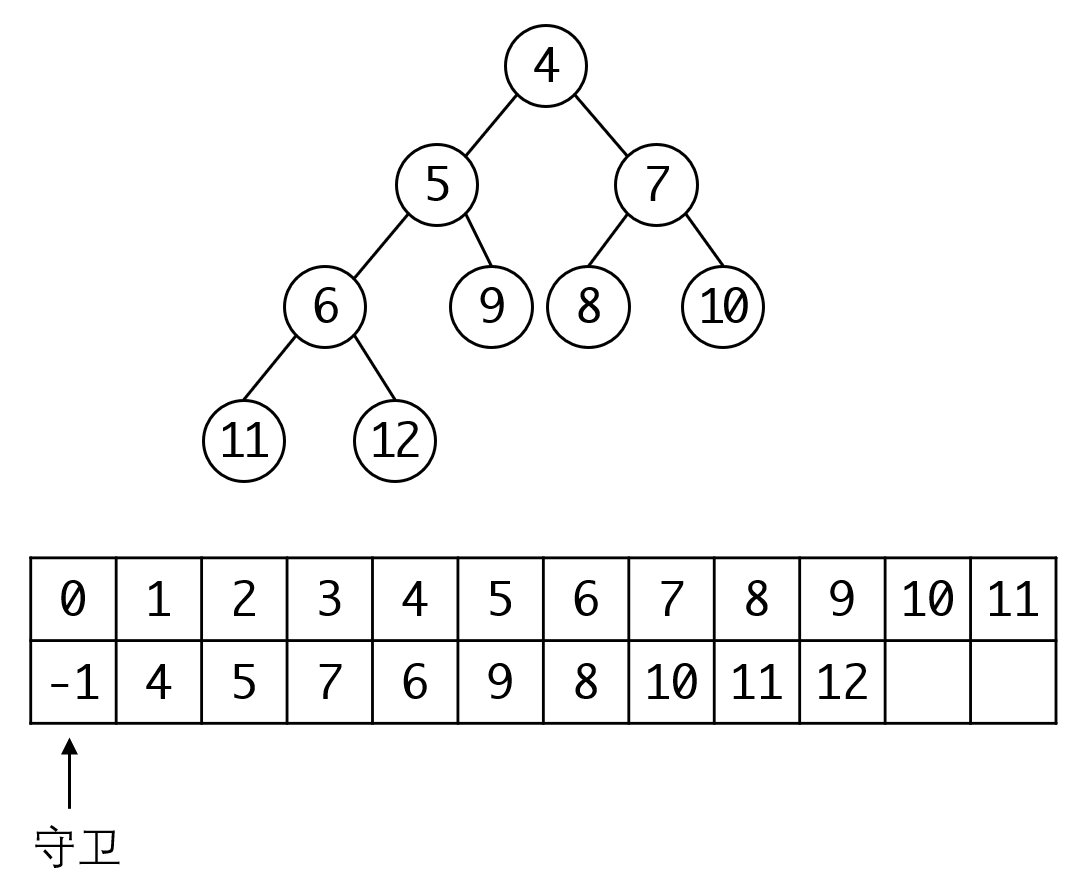
我们可以写出节点的相关关系:
- 父节点:
- 左孩子:
- 右孩子:
需要强调的是,我们对堆的操作,只会在顺序表(数组)上进行,所以这棵树只是逻辑上存在。
堆的插入
当插入新元素时,根据完全二叉树的要求,我们需要将节点放置在所有节点的后一位,保证排列中没有空位。我们假设插入1,可以得到这样的结果:
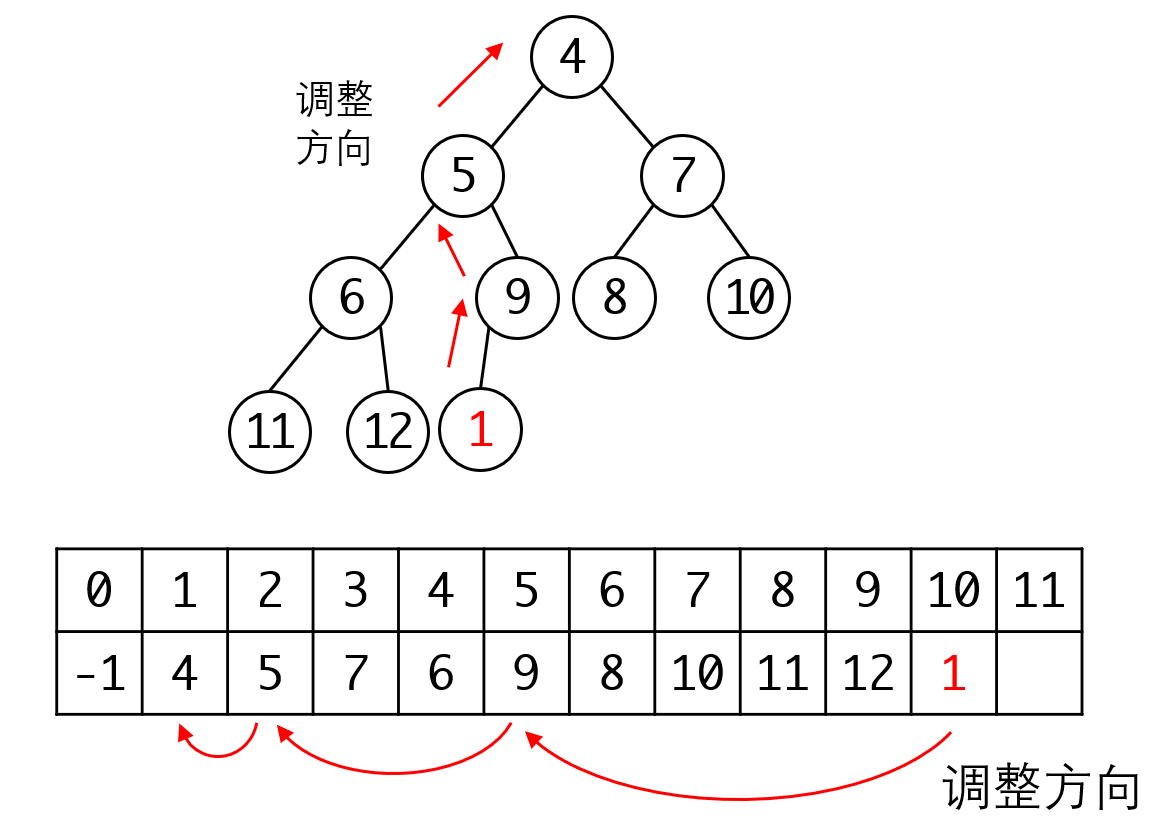
此时堆处于不平衡状态,我们需要调整,调整的从插入的节点开始,向上不断回溯他的父节点。如果节点比父节点小则交换两个节点,直到父节点比他小为止:
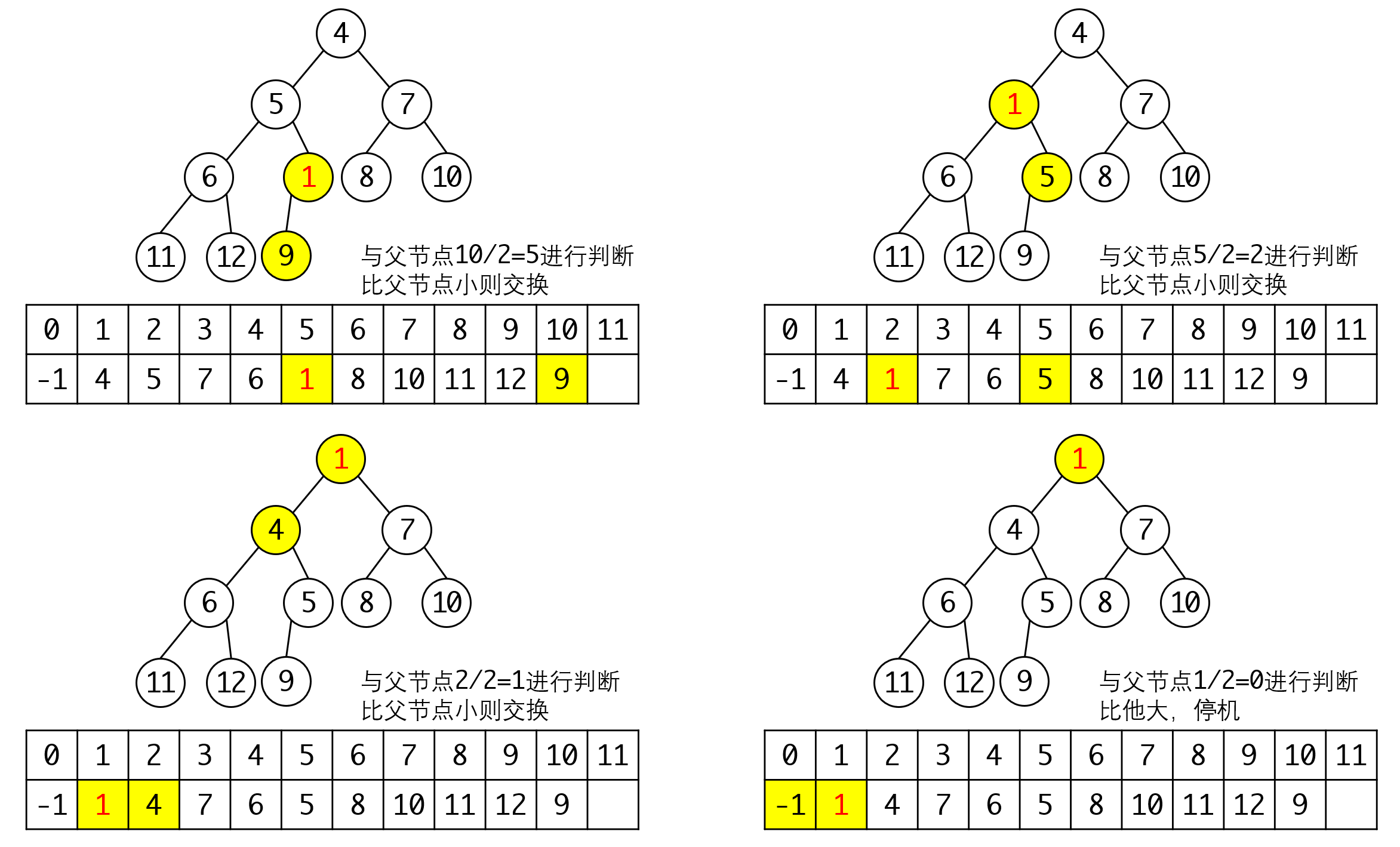
详细过程见上图。从这里我们可以看出0号守卫节点的用途。因为这个数字是最小值,所以任意节点在上溯到这个节点时,就会一定会停机,从而保证我们的回溯不会越界。
堆的删除(弹出)
我们希望从堆里取出的是最小的元素,根据堆的性质,这个元素就是树的根。但我们不能直接将这个元素取出,这样就破坏了完全二叉树的形态了。我们先将他与最后一个元素进行交换,然后再删除最后一个元素:
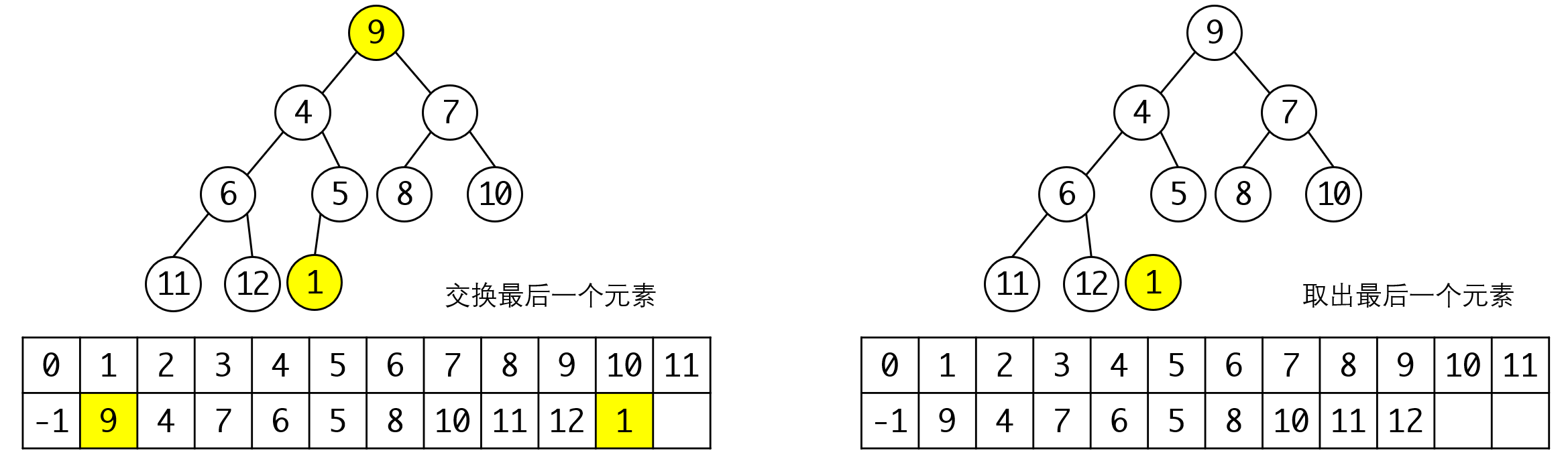
这样我们保留了完全二叉树的形态。但堆处于不平衡的状态,此时我们需要从上往下进行调整。
从下往上调整时,父节点只有一个,很容易进行判断。但从上往下时,子节点则有两个,要如何取舍呢?根据堆的性质,我们需要对比两个节点的大小,选择其中小的那个与待处理节点进行交换。
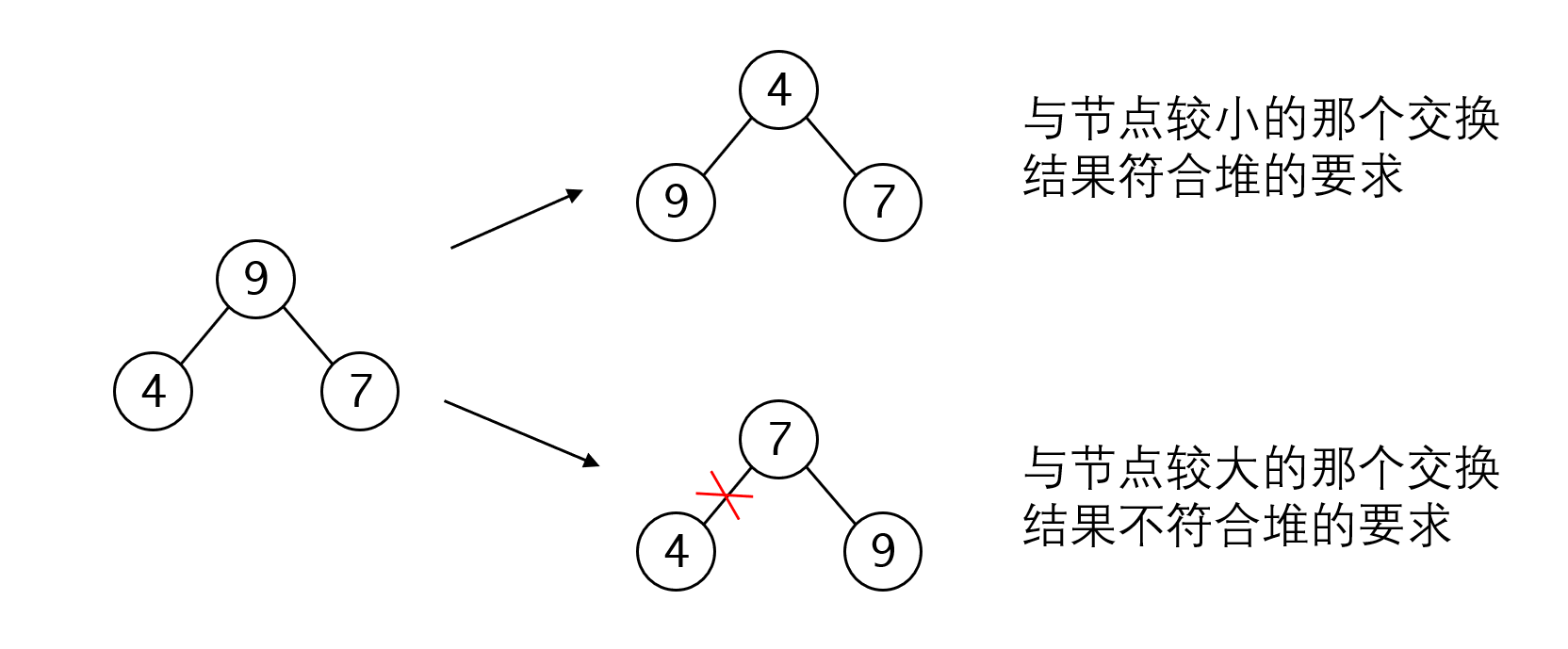
如此我们可以得到整个调整的过程:
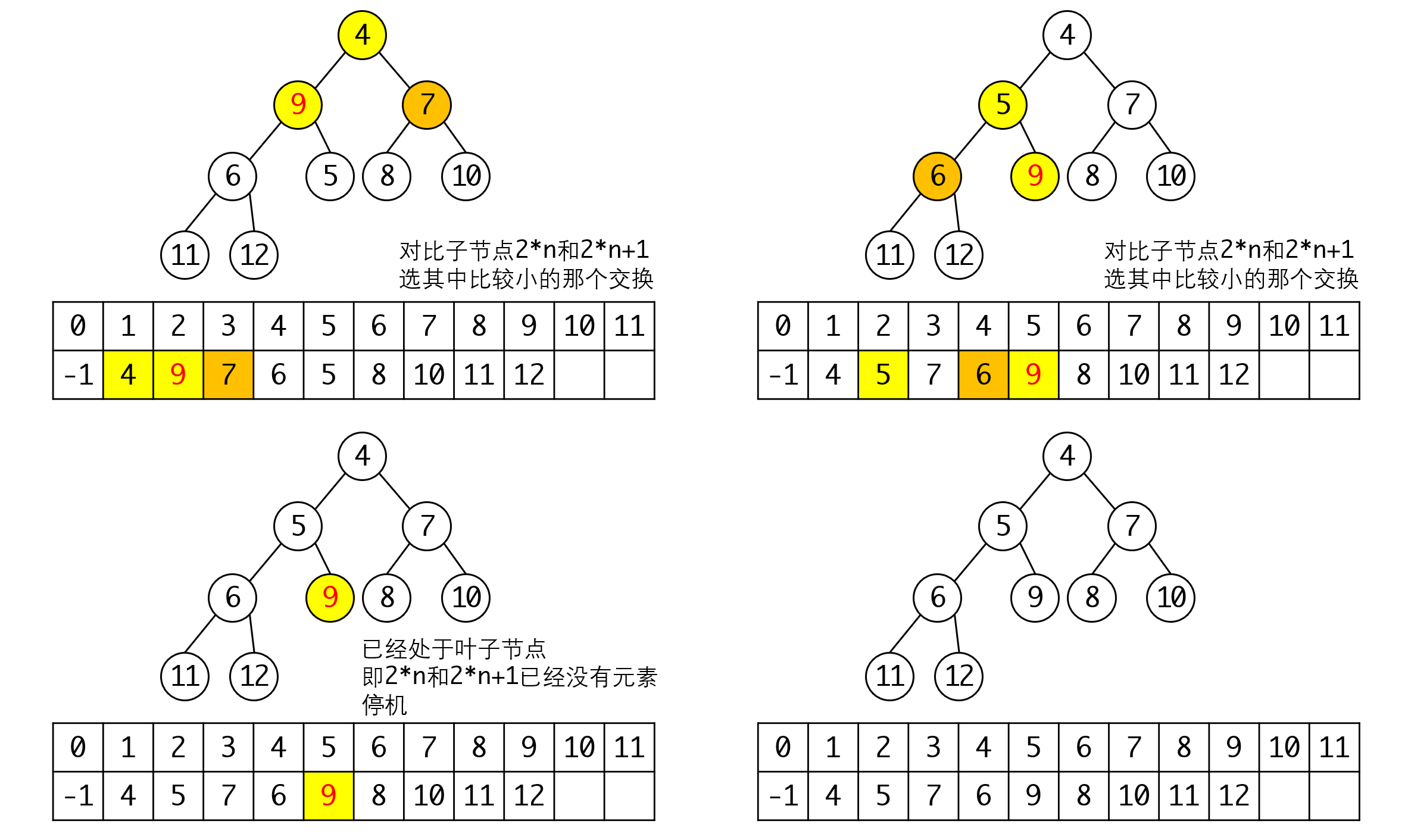
需要再次强调的是,上述过程中,树只是逻辑上存在,我们调整节点的过程,都在数组上进行。这使得我们可以快速地对节点进行处理,而不用频繁地进行内存的分配和销毁。因此堆是一种对于内存管理比较友好的数据结构。
堆操作的复杂度
根据堆的性质,极值永远处于堆的顶部,而我们需要的正是这个极值。因此获取数据的复杂度是。
对于插入和删除而言,最坏的情况是要从底向上,或者从顶向下穿过整棵树的高度。对于二叉树来说,树的高度是,因此插入和删除的复杂度是。
由此我们可以看到,堆在插入和删除时,都拥有的复杂度,是优于使用顺序表的的,所以一般来说,堆是实现的优先队列最合适的数据结构。