AVL平衡树

BST树的搜索效率、插入和删除的复杂度都可以达到$O(lgon)$，但这只是理想化的情况。我们设想一下这种场景；依次插入1，2，3，4，5，和插入3，2，4，1，5，形成的BST树会是怎么样一种情况：

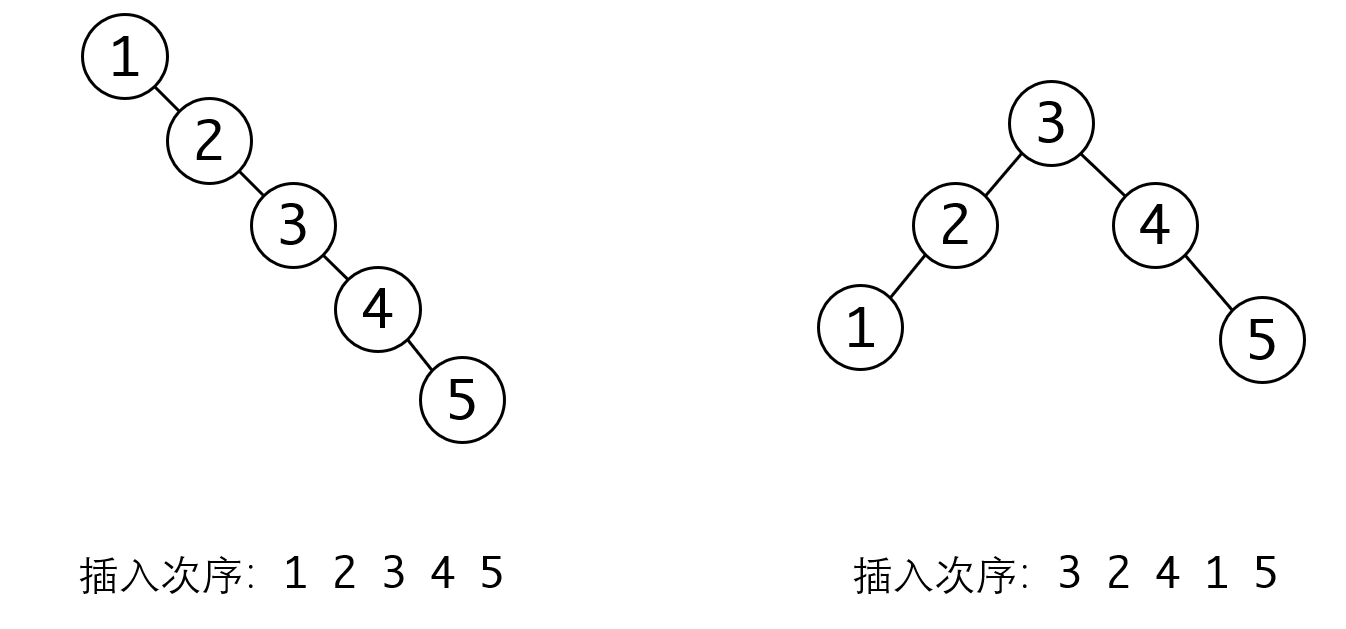
显然在右边的树上搜索会比左边的快，左边的树实际上已经退化成链表，操作的效率都会退化成$O(n)$，这显然不是我们想要的。造成这种现象的原因在于左边的BST不平衡，所有节点都被挂在右子树上。所以我们希望构建的树要尽可能的平衡，像右边这样，这就是平衡树。

我们先看最平衡的状态是哪种，显然是满二叉树，严格满足树高=$log_2n$，可以满足搜索为$O(logn)$的效率。但这种情况是很难满足的，因为满二叉树要求节点数必须满足$2^n-1$的要求。

如果我们退而求其次，要求左右子树的高度差不能超过1，那么树就可以接收任意数目的节点。这就是AVL（以两位发明人Adelson-Velskii和Landis的名字命名）平衡树。

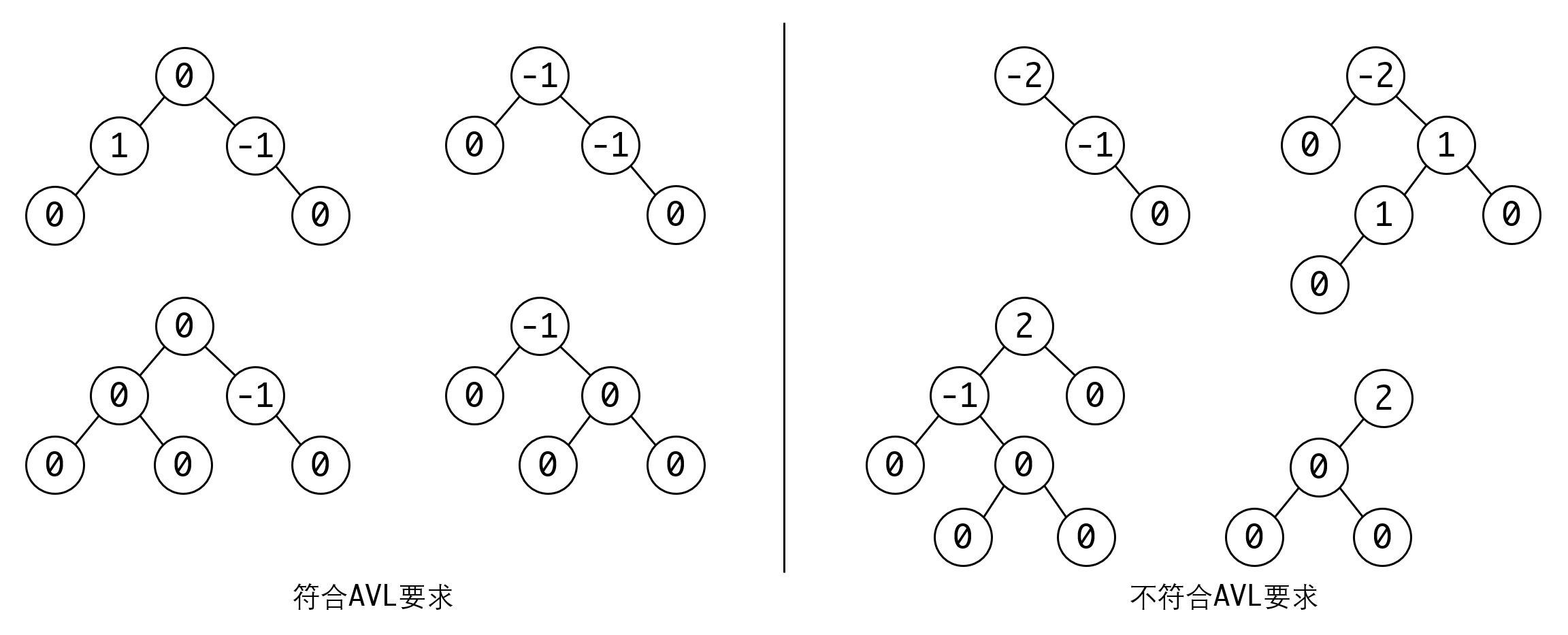
我们把左子树高度-右子树的高度称为平衡因子。那么对于AVL树来说，平衡因子只能为-1，0，1这三个值：

AVL的插入

不平衡的类型

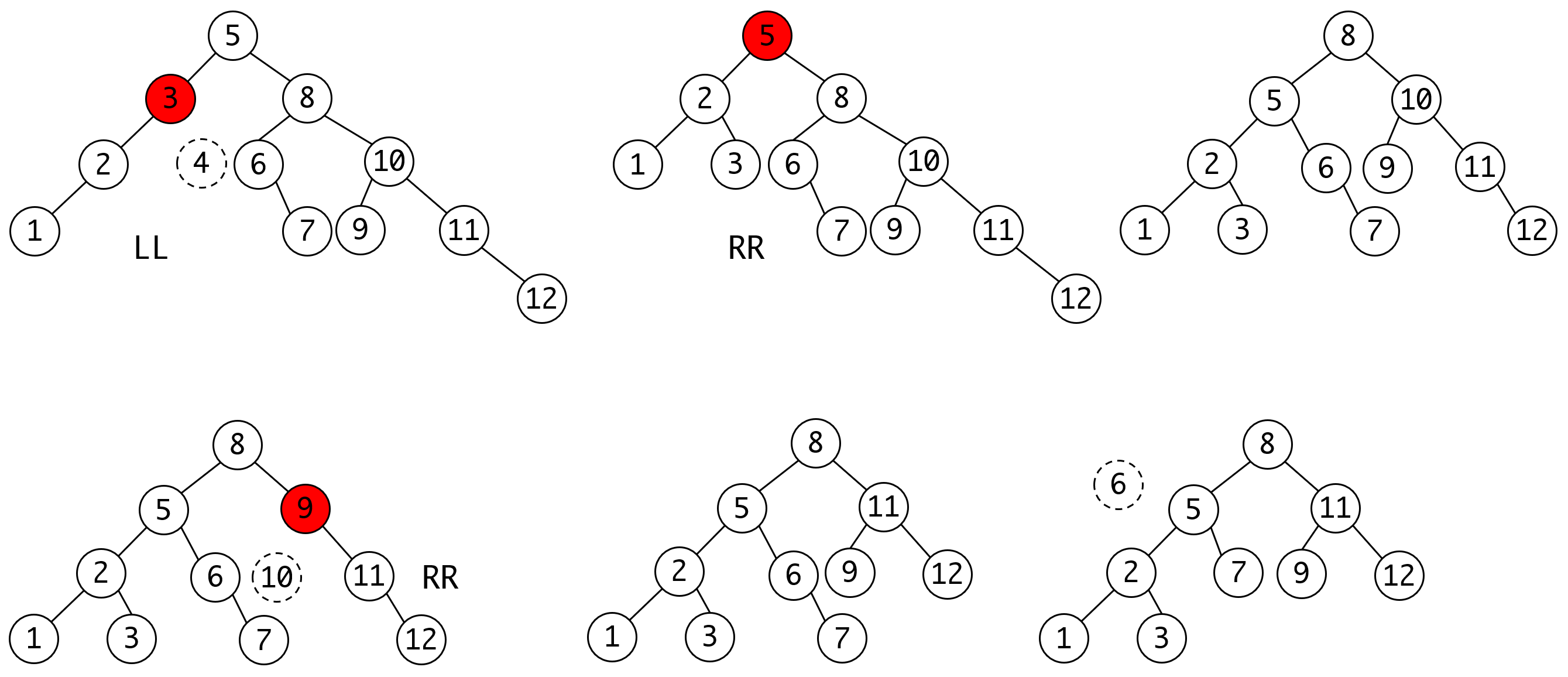
我们先看插入的情况，我们不讨论插入不破坏平衡的情况，只看破坏平衡会有几种可能：

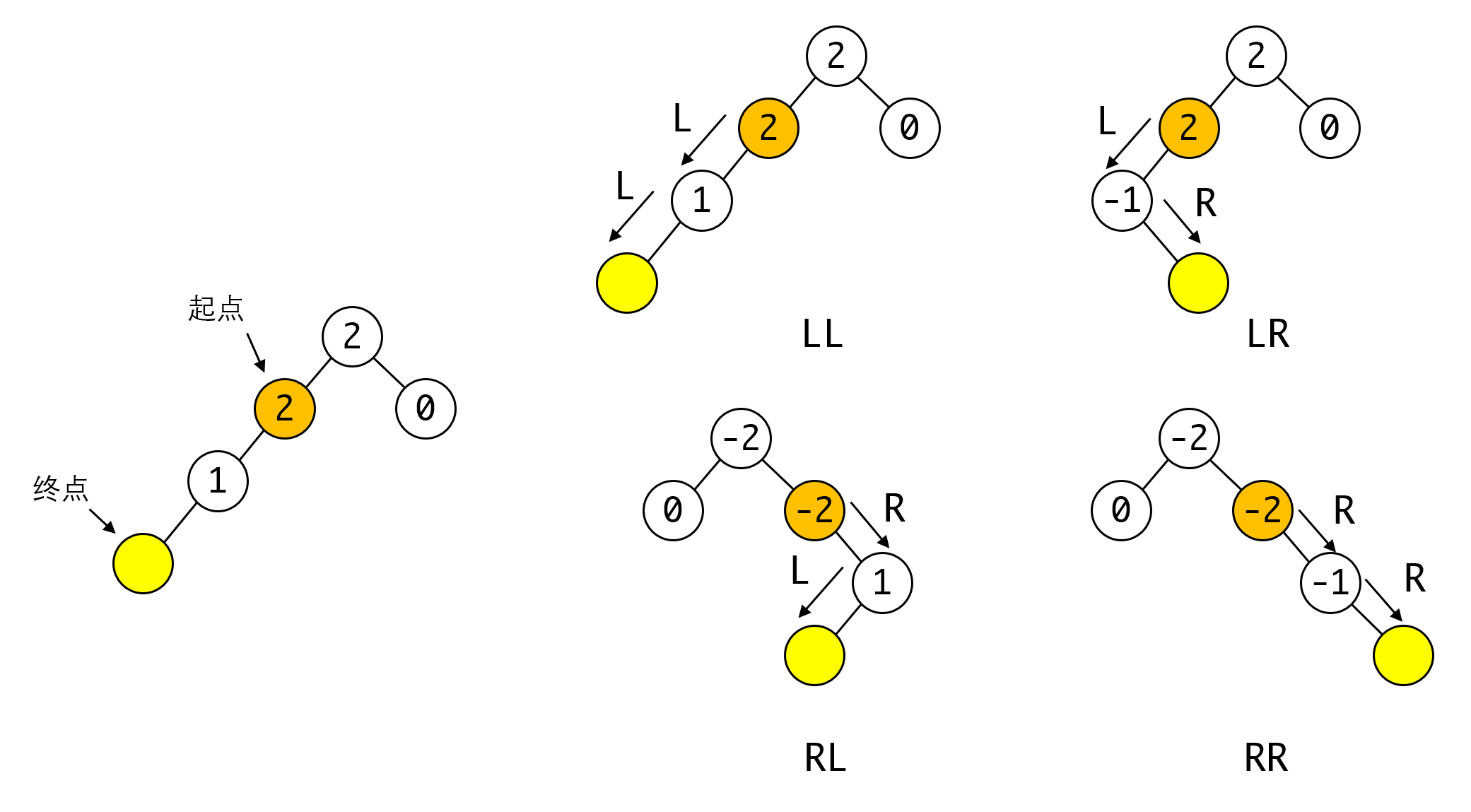
黄色的部分代表新插入的节点。注意由于插入前树处于平衡状态，所以只可能出现上述的四种情况。

我们针对这四种情况进行命名。以插入节点向上上溯的第一个不平衡节点为起点，以插入节点为终点，共有两条路径，根据这两条路径的方向可以定义四种类型：

重平衡

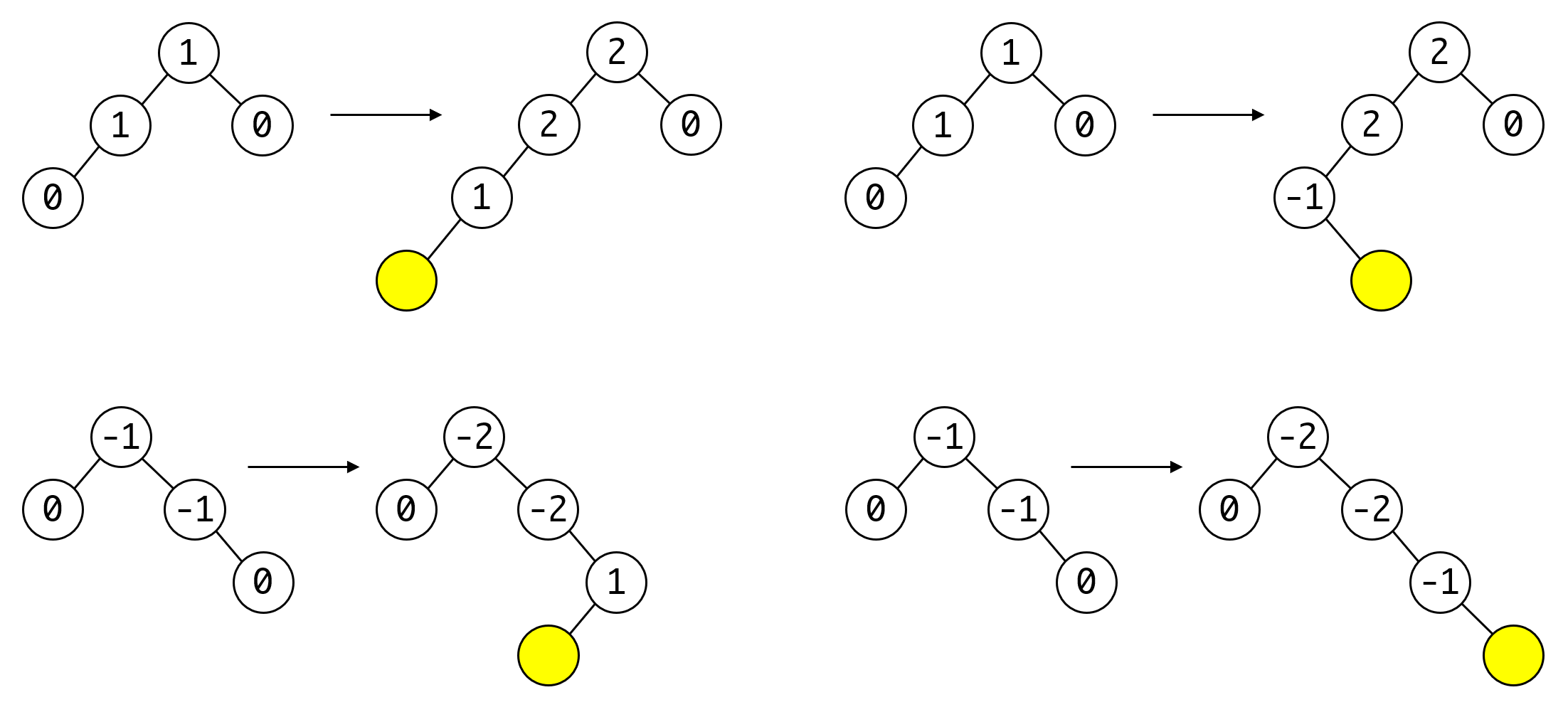
针对这四种情况我们可以设计这样的重平衡策略：

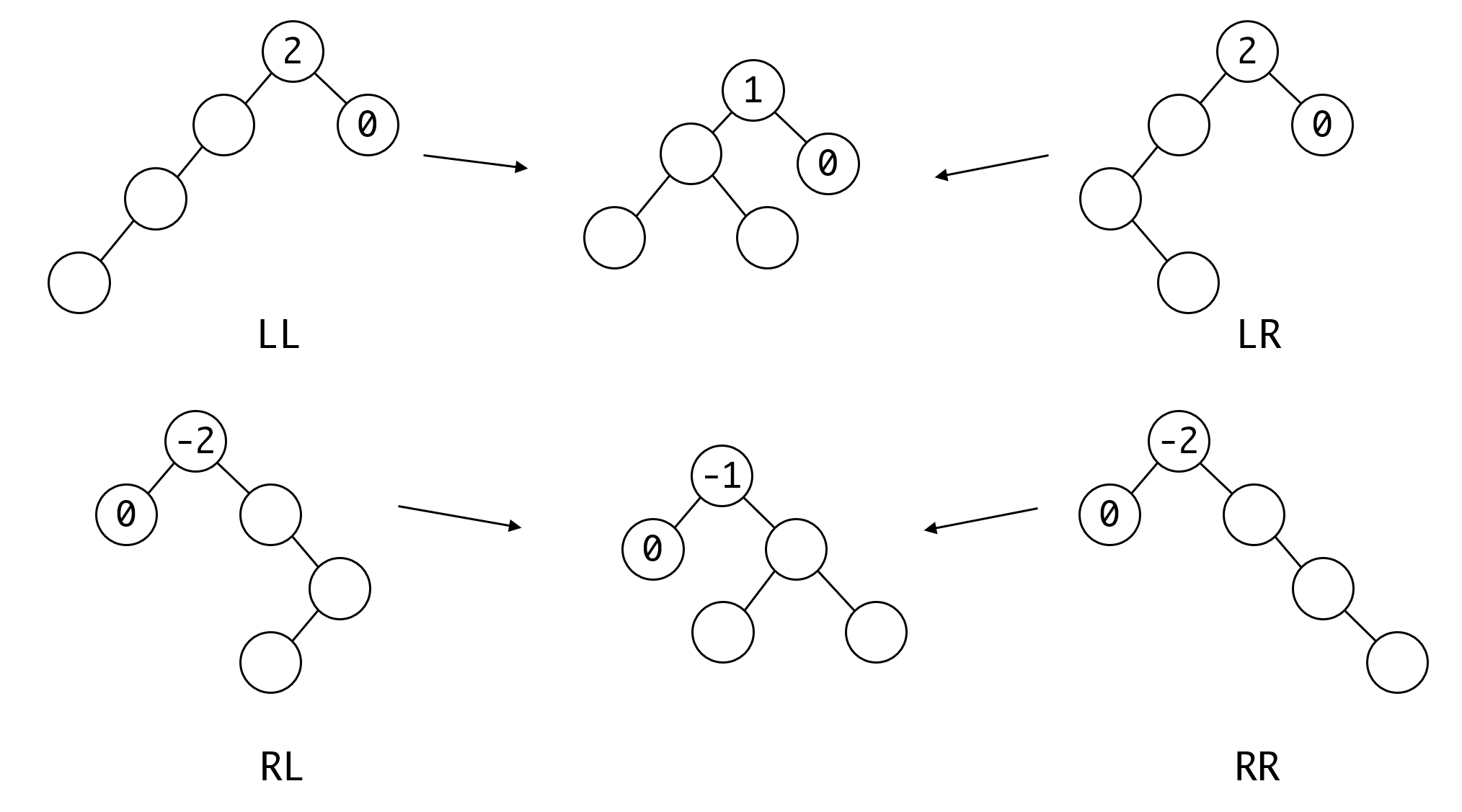
再进一步简化的话，我们会发现，其实是把这四种情况都转换为同一种构型：

剩下的就是新旧节点的关系如何映射，这可以由节点的大小关系来确定，上图中的1，2，3代表的三个节点有这样的关系1<2<3。只要按对应的关系进行映射即可。

子树的处理

如果节点带子树，则可以根据子树和节点之间的关系判断他们在新构型上的位置，这里要分两类情况讨论。

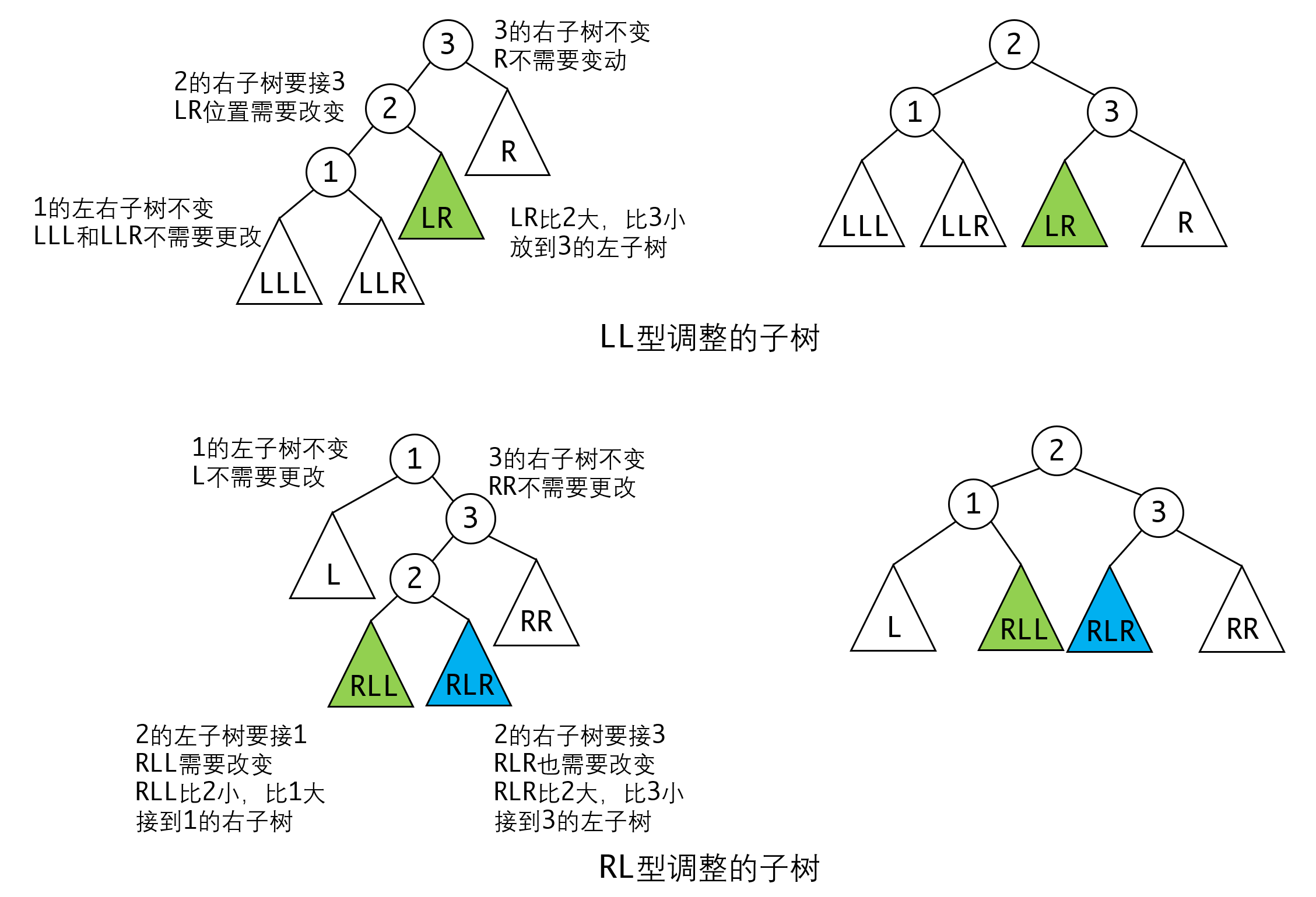
对于LL型，只有中间节点，也就是2这个节点，由于其右子树会接上3，因此其原来的右子树需要调整位置，因为这个子树比2大，比3小，所以应当接入3的左子树。同理RR也有类似的处理。

对于RL型，由于节点2的左右子树都要接上新节点1，3，他们的位置都需要调整。由于2的左子树比2小，比1大，所以应当放入1的右子树。2的右子树比2大，比3小，所以应当放入3的左子树。同理LR的处理方式也类似。

剩余的形状的调整，请各位自行画图，作为学习内容的巩固。

实现细节

我们还有一个问题没有解决，就是如何判断调整的类型。这要考虑我们处理的细节。

当我们插入一个节点之后，我们需要向上回溯并更新每个节点的平衡因子直到根节点。在这个路径上，当我们遇到不平衡节点时，我们就需要进行调整。我们有两种方式来判断调整的类型：

第一种，我们可以记录路径上的指针，即记录当前指针的前一个和前两个指针。然后通过这三个指针来判断他们之间的关系。

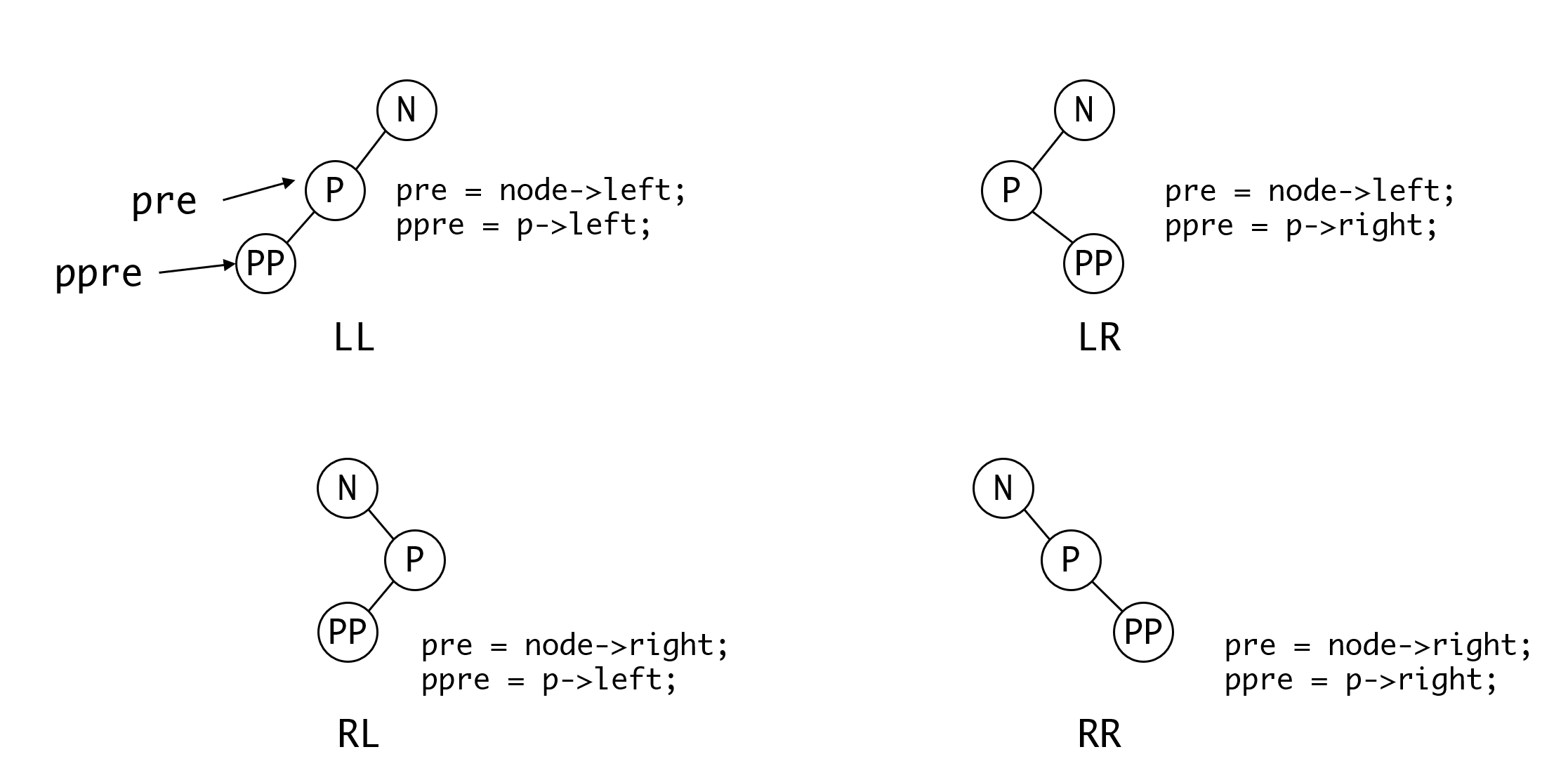
第二种，我们可以用插入的值和节点的大小关系以及平衡因子的值来进行判断。

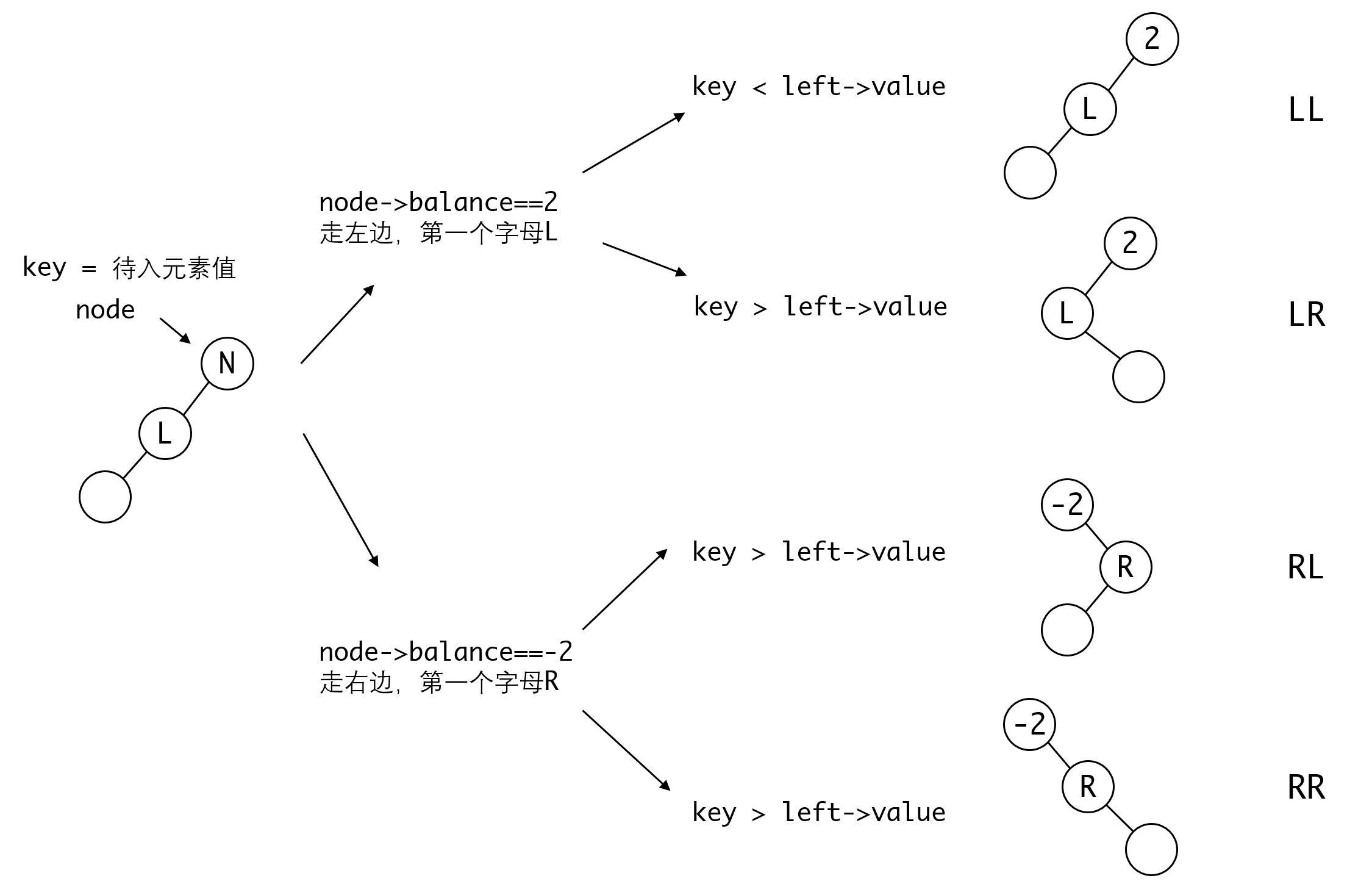
第一种判断方式需要在遍历过程中记录额外的指针，会有一些比较特殊的情况需要处理（空指针等）。第二种方式可以从不平衡节点往下判断，不需要额外记录指针，因此相对来说第二种方式的逻辑要简单一些。

习题

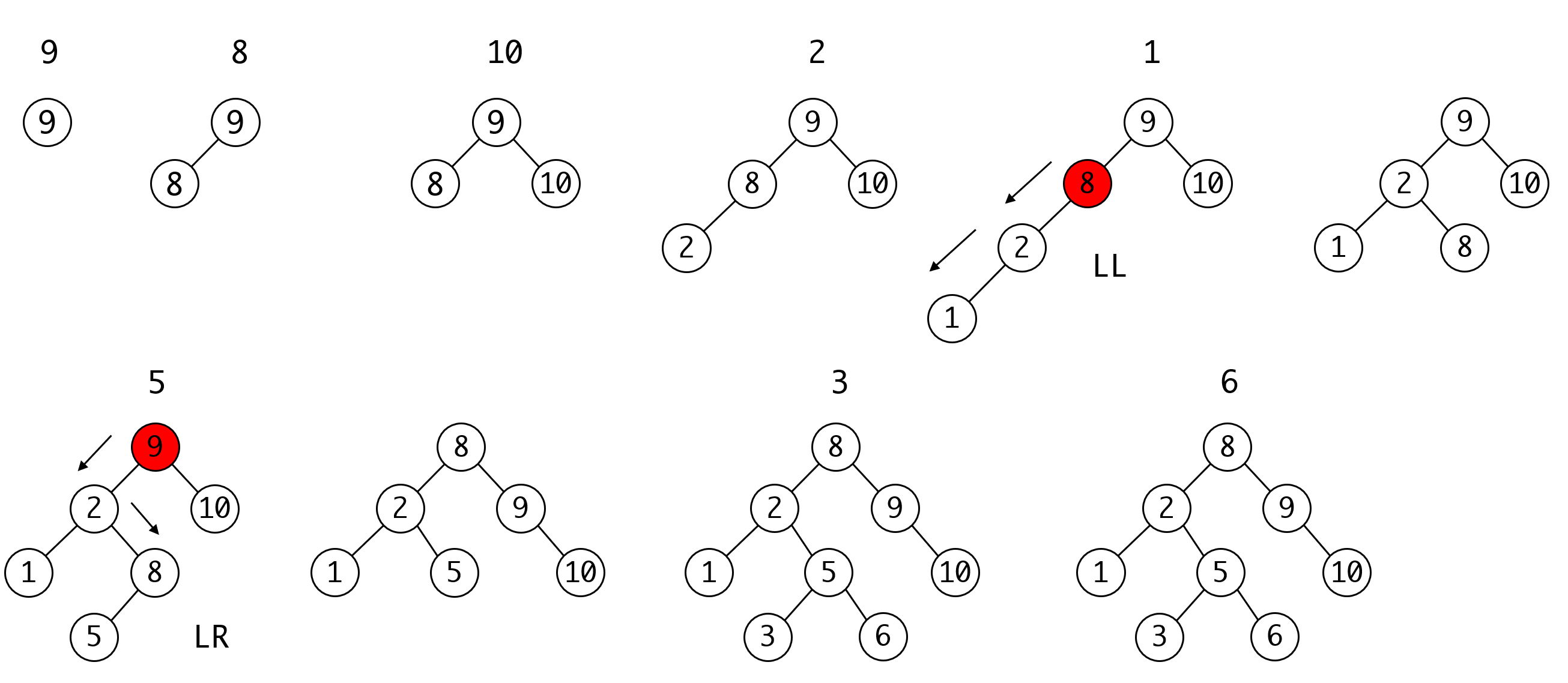
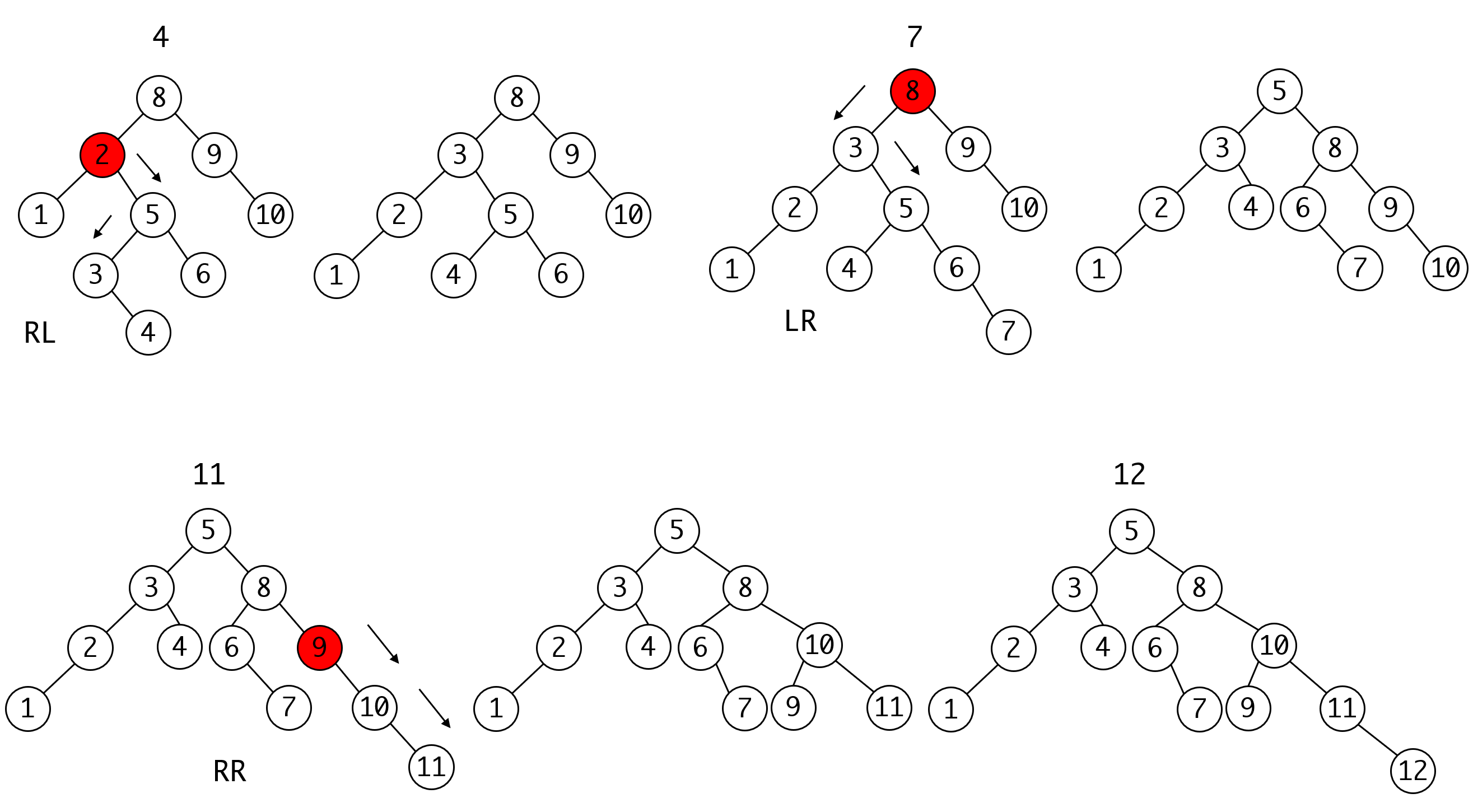
依次插入

9 8 10 2 1 5 3 6 4 7 11

请画出插入的过程

点击查看答案

AVL的删除

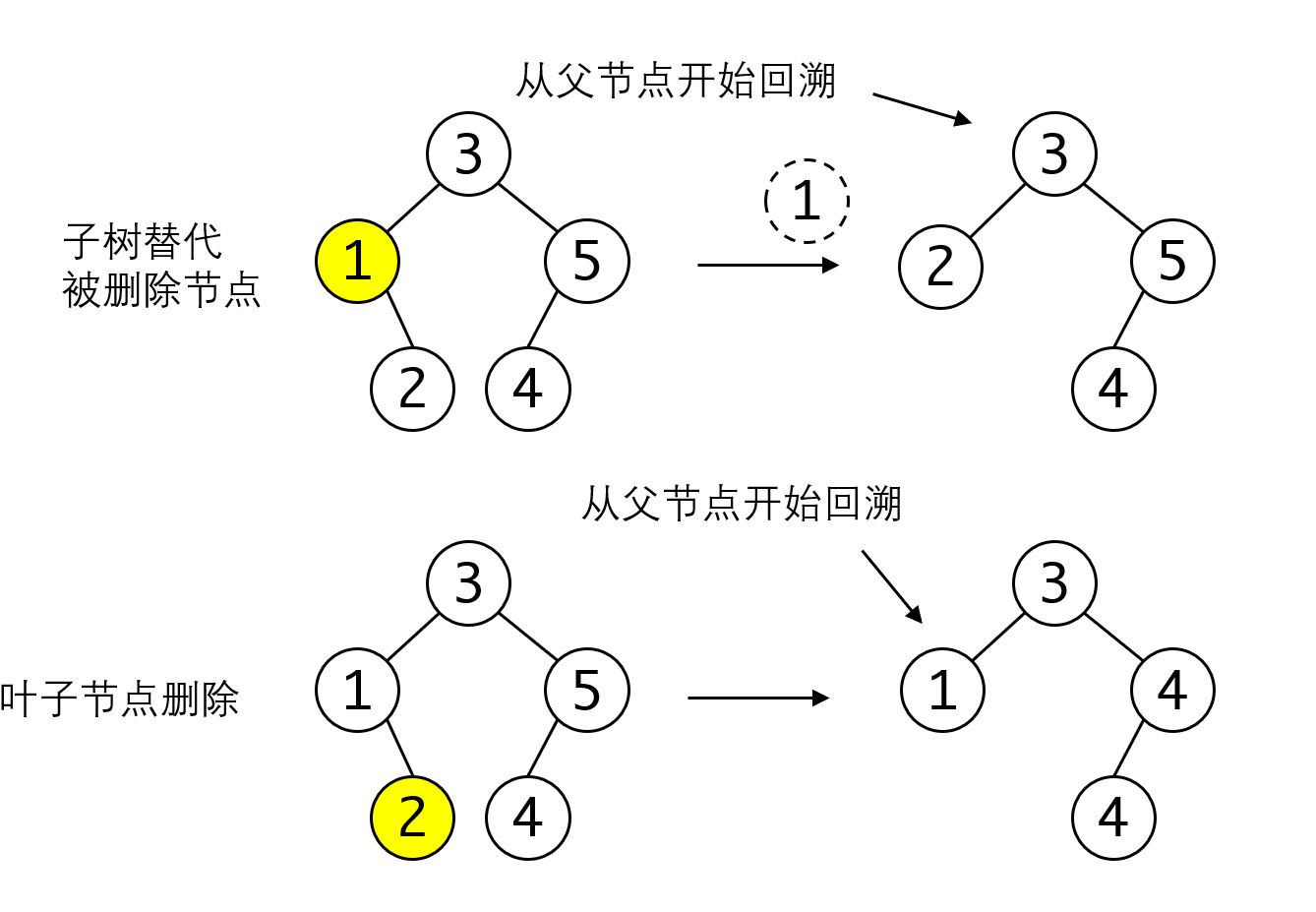
AVL的删除可以转化为插入的等价形式来处理。需要注意的一点是，根据BST删除的规则，假如待删除节点的左右子树都存在，应当将其与左子树的最大值或者右子树的最小值进行交换再执行删除。此时要从被删除的位置的父节点（也就是交换后的位置）开始回溯，而非从原始位置开始回溯。

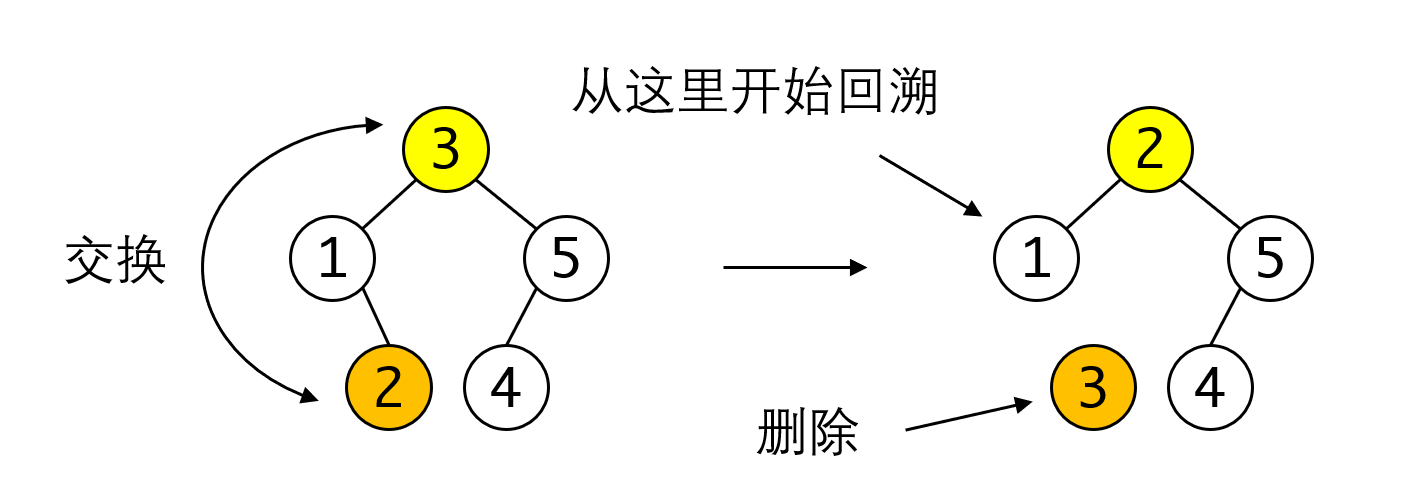
所以实际上回溯的类型是两类，一类从叶子节点开始回溯，另一类从某个非叶子节点开始回溯，但他们都可以看作从待删除节点的父节点开始回溯，再次强调要注意这里的待删除结点指的是经过交换之后会被删除的节点。

不平衡的类型

我们先看四种等价形式：

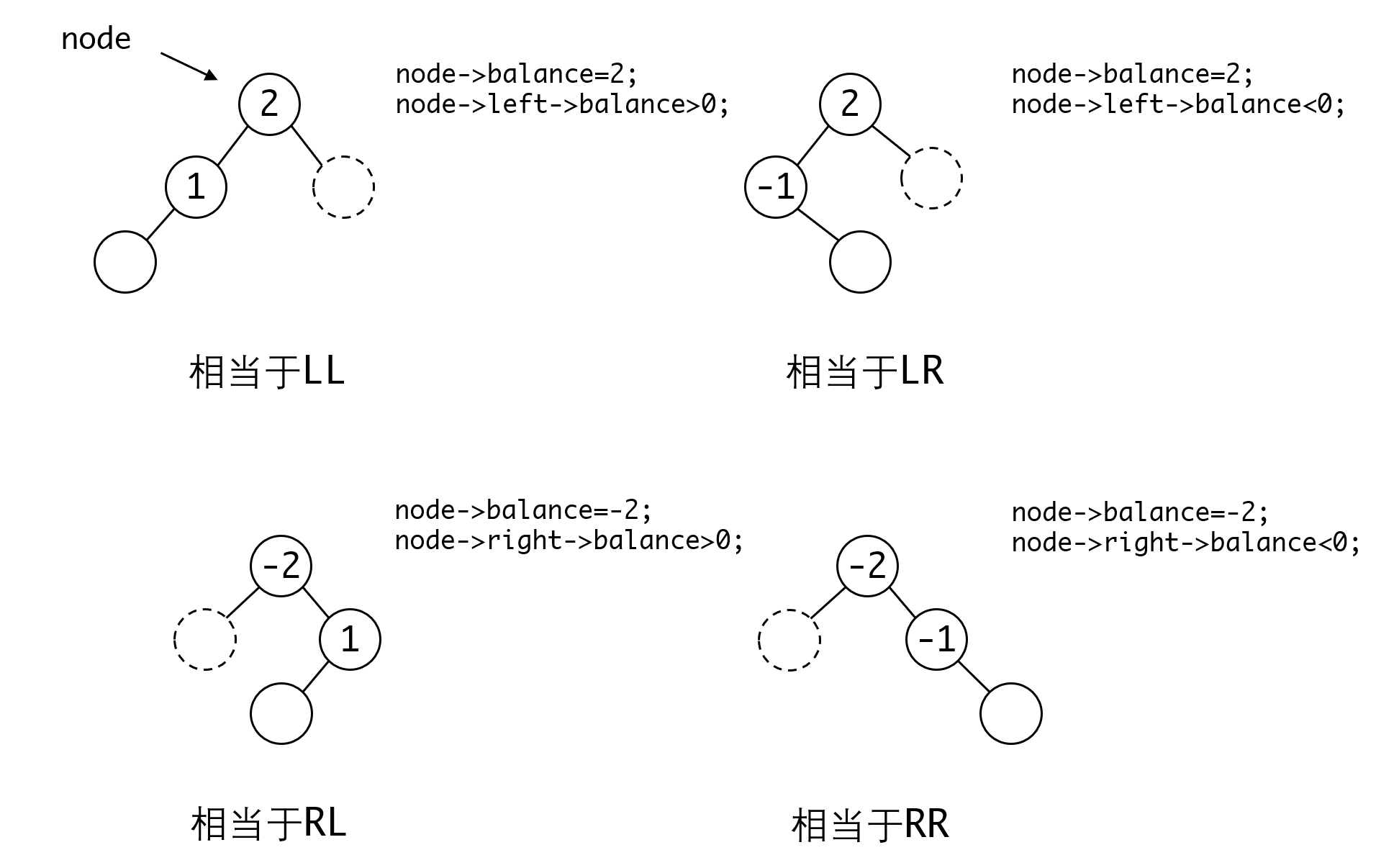
他们的判断依据也非常简单，利用不平衡节点的平衡因子和他对应子树的平衡因子进行判断即可。

但要注意的是，删除可能出现下面两种情况：

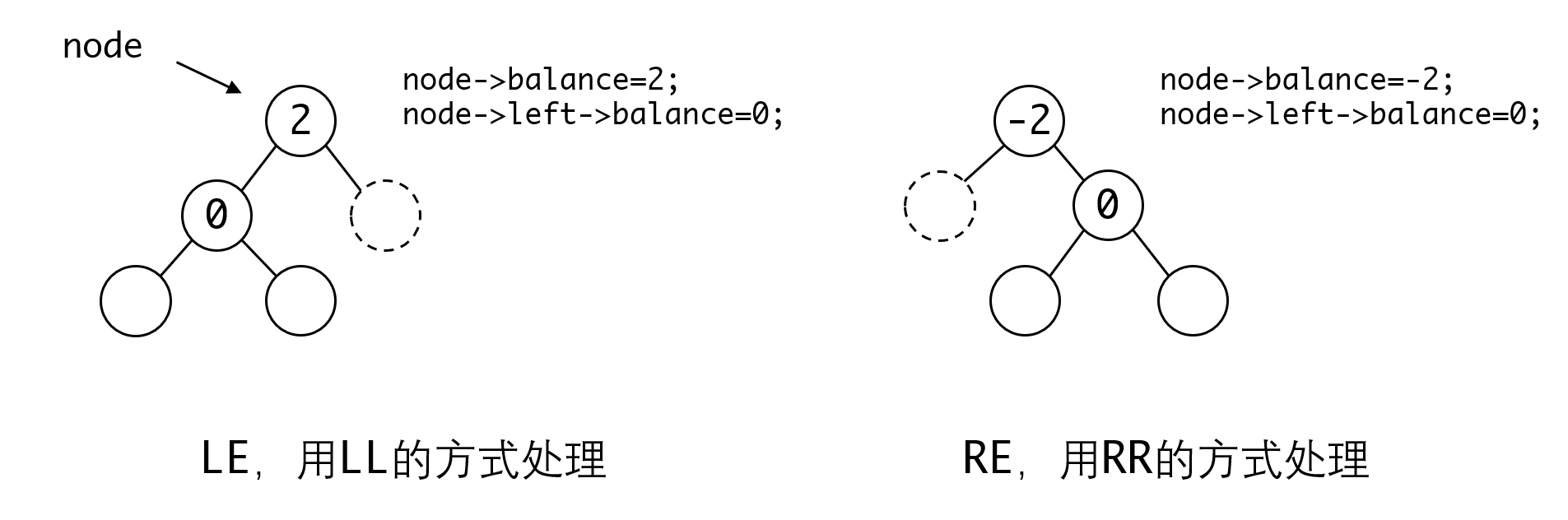
这两种情况在插入时是不可能发生的（为什么？），但这两种方式很好处理，不论用LL（RR）还是LR（RL）的处理方式都可以让他们重新平衡，我们选择比较简单的LL和RR来处理即可。

向上回溯

节点删除和节点插入的另一个区别，也可以说最大的区别在于，节点删除是需要向上回溯的。

我们前面在插入的部分没有讲是否需要回溯的问题，这是因为节点插入只要处理了第一个不平衡的节点，整棵树就平衡了（为什么？你可以试试看能不能构造这种情况的反例）。但节点的删除不同。看下面的删除：

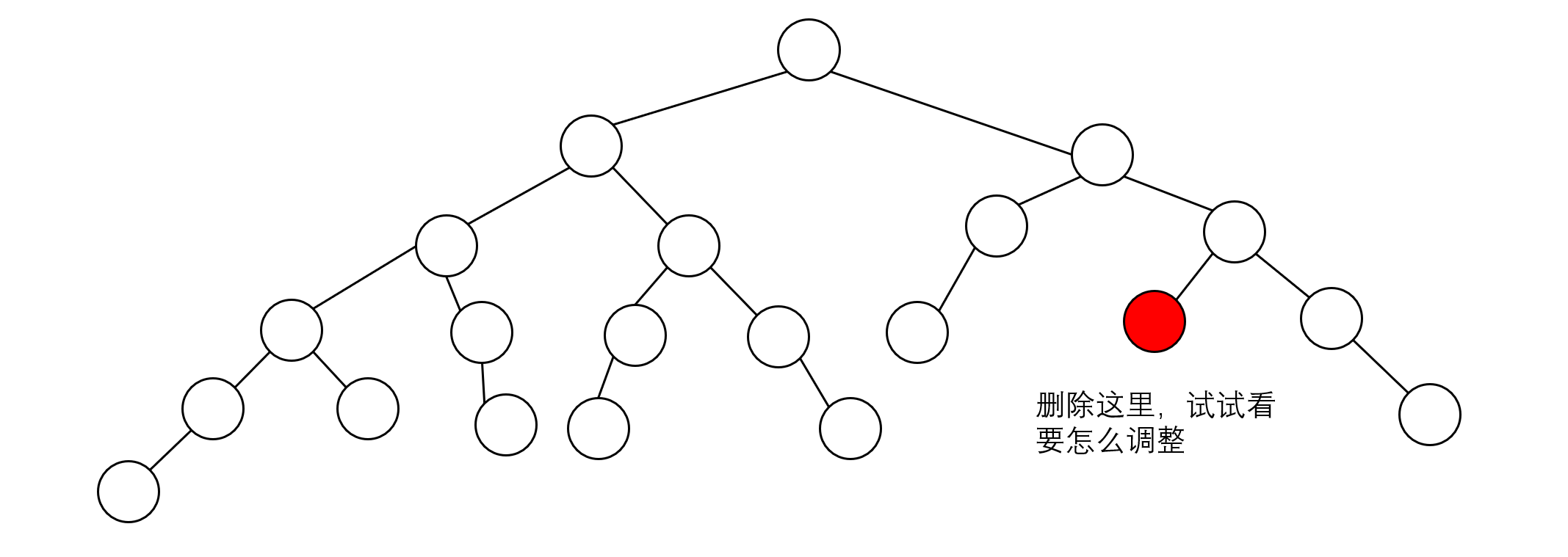
在删除节点之后，出现了不平衡：

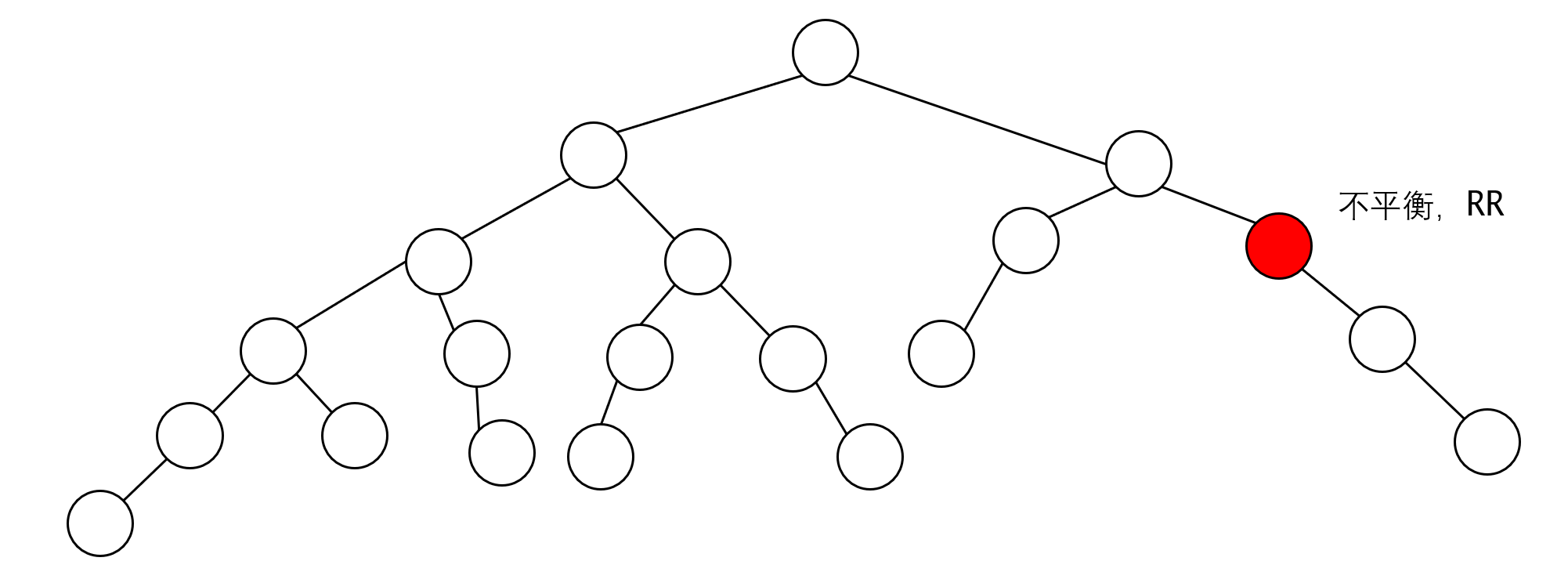
对节点进行调整：

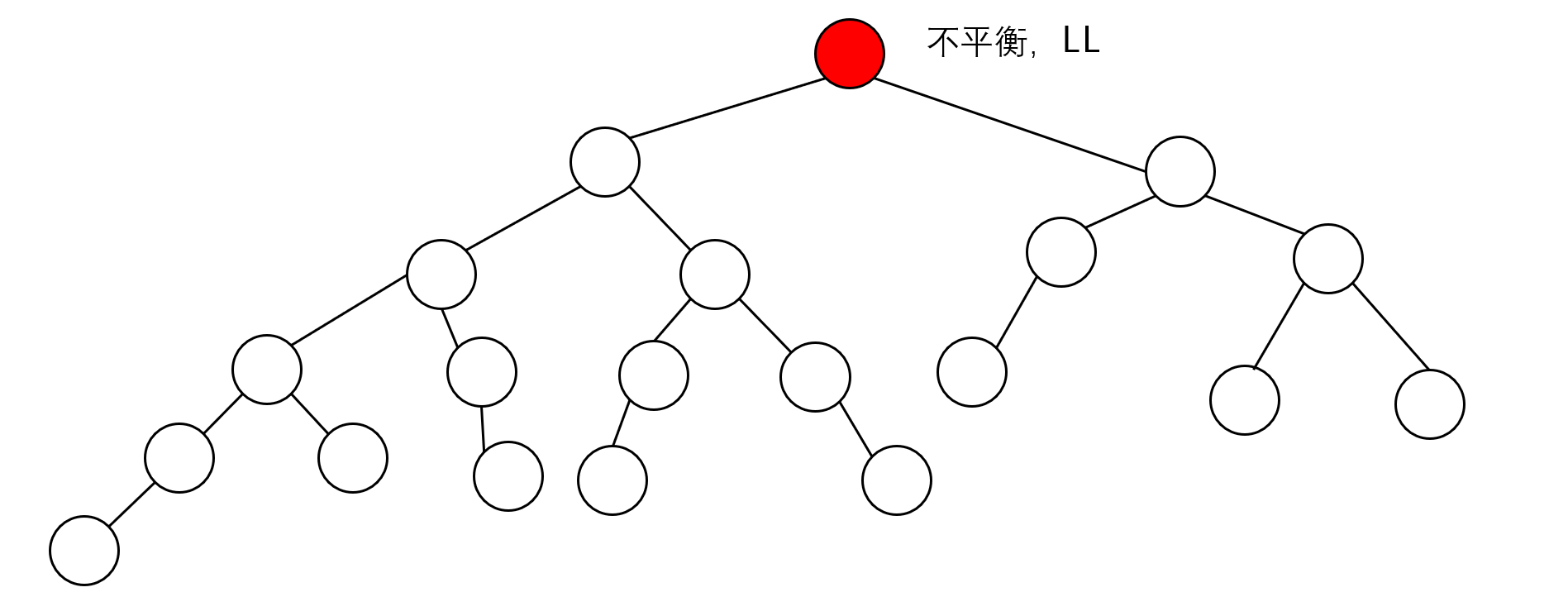
可以发现他的父节点又不平衡了。

删除节点时，由于子树高度一定是逐步缩减的，有可能产生连锁反应，所以需要一直上溯到根节点，才能保证完全平衡。

习题

添加的那棵树，依次删除下面节点的结果，其中我们假定两个孩子节点都在时，采用交换左边最大节点的办法来处理。

4 10 6 7 1

点击查看答案