基础排序

简单选择排序

算法描述

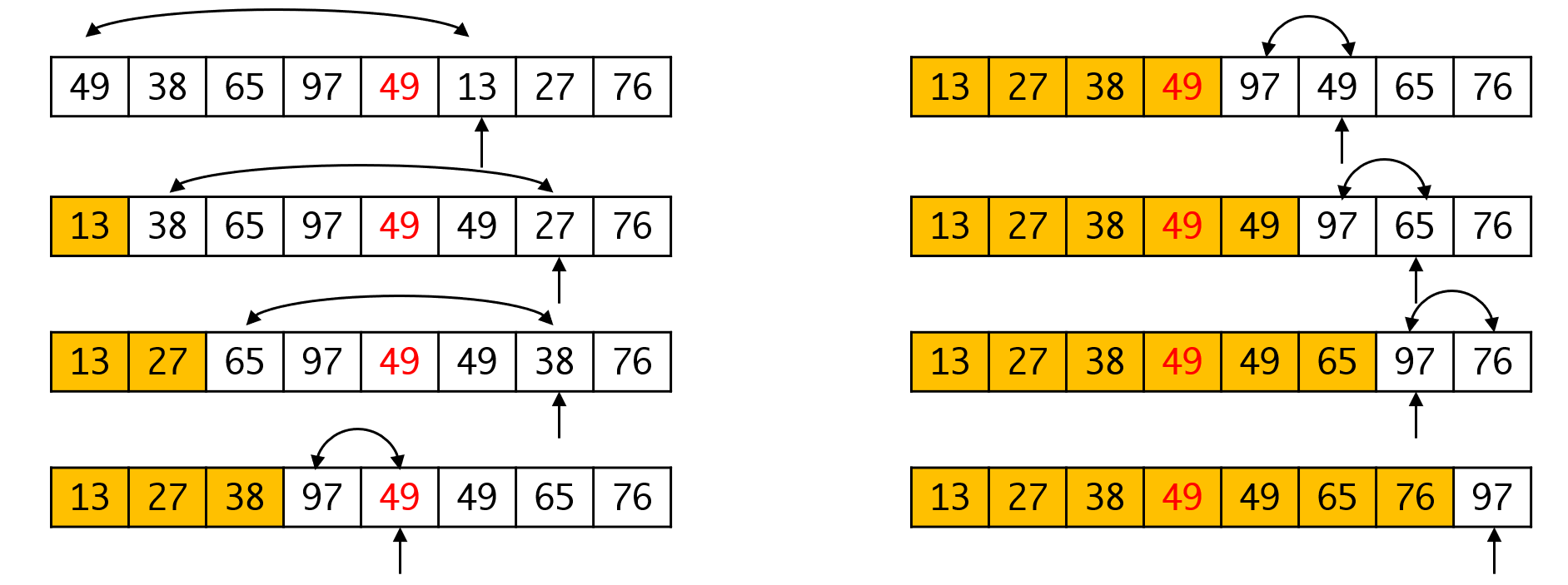
选择排序是大家最容易想到的排序算法。他的思想很简单，每次都选最小的元素与放在首位，之后缩小排序的范围，执行n-1轮之后，整个序列就是有序的了。

当然如果我们每轮都选最大的元素放在末尾也是可以的，过程请大家自行推导。

算法分析

时间复杂度：从算法的描述中我们可以看出，选择排序算法会执行n-1轮，而第i轮我们都需要在i个元素中寻找其中最小的元素，这个操作的时间复杂度是$O(i)$。因此我们很容易得到整体的时间复杂度是$O(n^2)$。

这一复杂度并不会因为数据的不同排列而有所变化，因为我们每次都要在剩余的元素中寻找最大的元素，即便序列已经有序，我们也无法从算法执行的过程中获得这一信息。因此其最好、最坏和平均时间复杂度都是$O(n^2)$。

空间复杂度：操作过程中我们并未开辟新的空间，因此空间复杂度是O(1)。

稳定性：从上面的过程中我们明显能看出选择排序算法是一个非稳定的排序算法。然而实际上这是一个误解。我们选择了将最小元素与首位元素进行交换的做法。这一做法会破坏元素之间的相对关系，从而导致排序结果的不稳定。这从第一次交换就可以看出了。

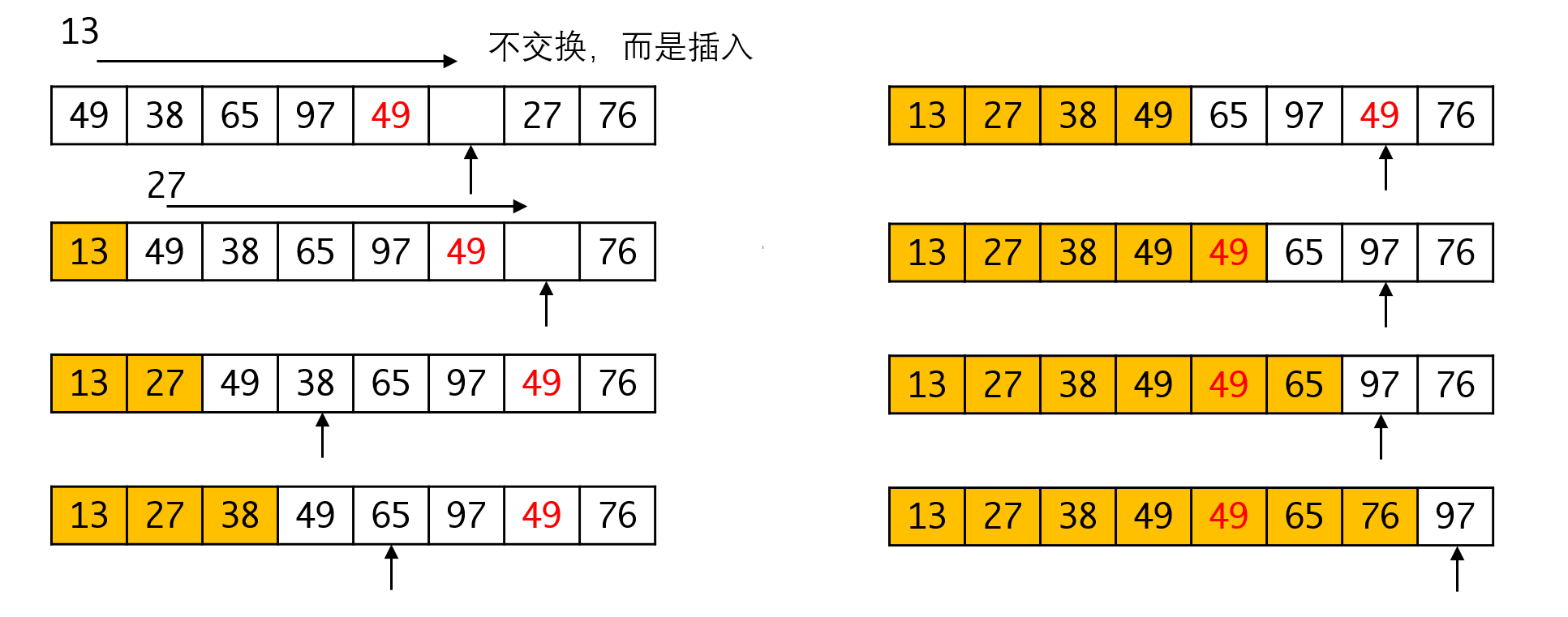
那么有没有办法让这个过程稳定呢？有的，如果我们不采用交换的方式，而是整体移动整个序列，再将最小元素放入，则可以保证排序的稳定性。这一过程实际上相当于将元素插入到序列的最前端，在这个过程中序列是整体移动的，元素的相互关系就得以保留，我们可以得到一个稳定的算法。

那么古尔丹，代价是什么呢？

如果我们不需要付出代价就可以得到一个稳定的算法，我们就不需要先讲交换法了。那么代价是什么呢？

如果待排序的序列是顺序表，那么插入的代价很明显，是一个$O(n)$级别的操作。而如果采用直接交换，这个代价就降低到$O(1)$。虽然并不会改变总的复杂度，但交换显然要比插入快。

适用范围：选择排序每一趟我们都需要遍历整个序列，并不存在随机访问的情况，因此顺序表和链表都可以跑。实际上由于链表执行插入的时间复杂度是$O(1)$，在链表上维持一个稳定算法的代价比顺序表的代价要小。

冒泡排序

算法描述

如果要选一个排序算法作为排序的牌面，那一定是冒泡排序，很多人可能都没听说过其他排序算法，却一定听说过冒泡排序，可能是因为他的名字真的非常形象。

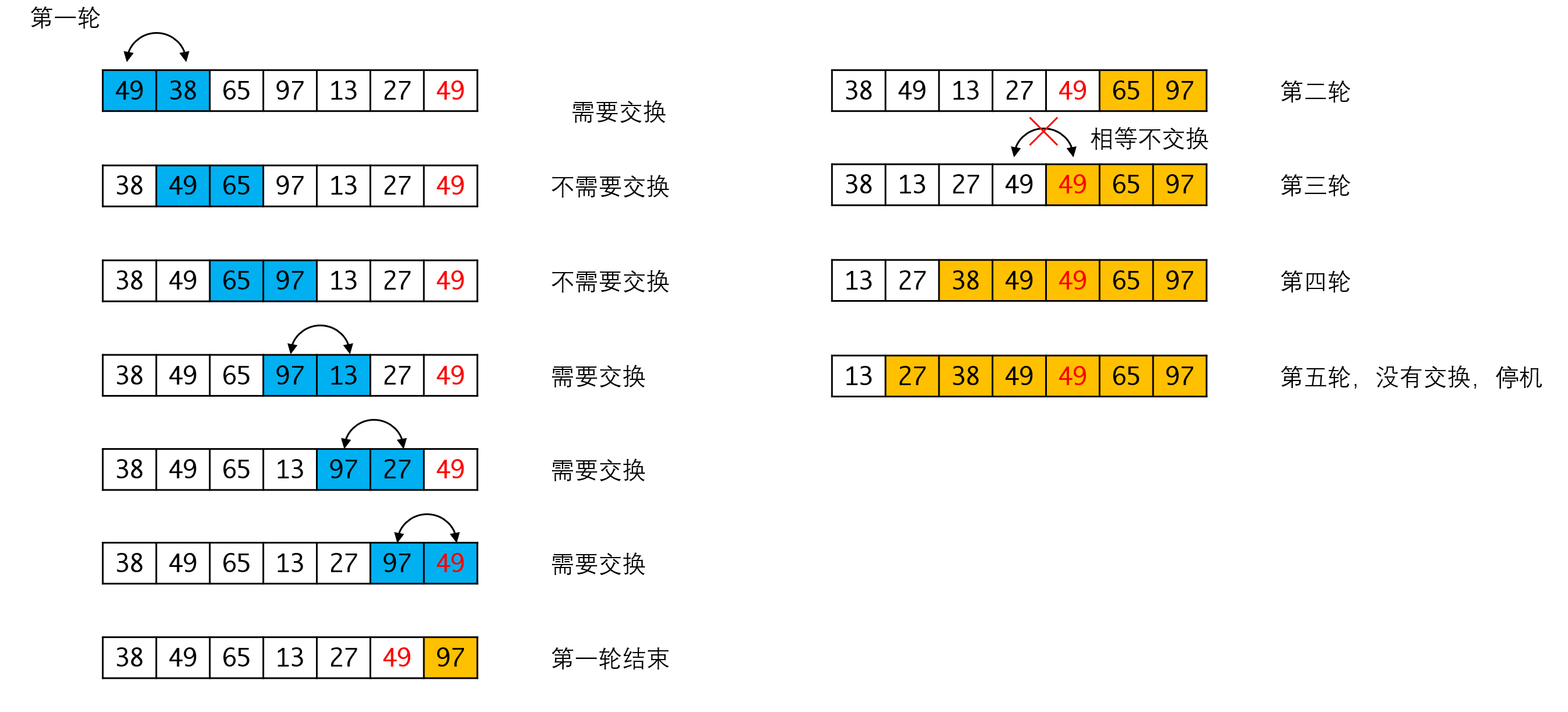
冒泡排序是一种交换排序算法。其算法的思想是，不断比较相邻两个元素的大小，如果不符合序列要求，则交换。这样每一趟都能保证把最大的那个数字“拱”上去。这就像水里的气泡，大的那个总会比小的气泡上升的更快，这就是冒泡排序这个名字的由来。

算法优化

你可能注意到我们中间实际上缺了一轮，即第三轮和第四轮中我们跳过了一轮，这是冒泡排序可以进行优化的点，考虑下图左边的这个序列：

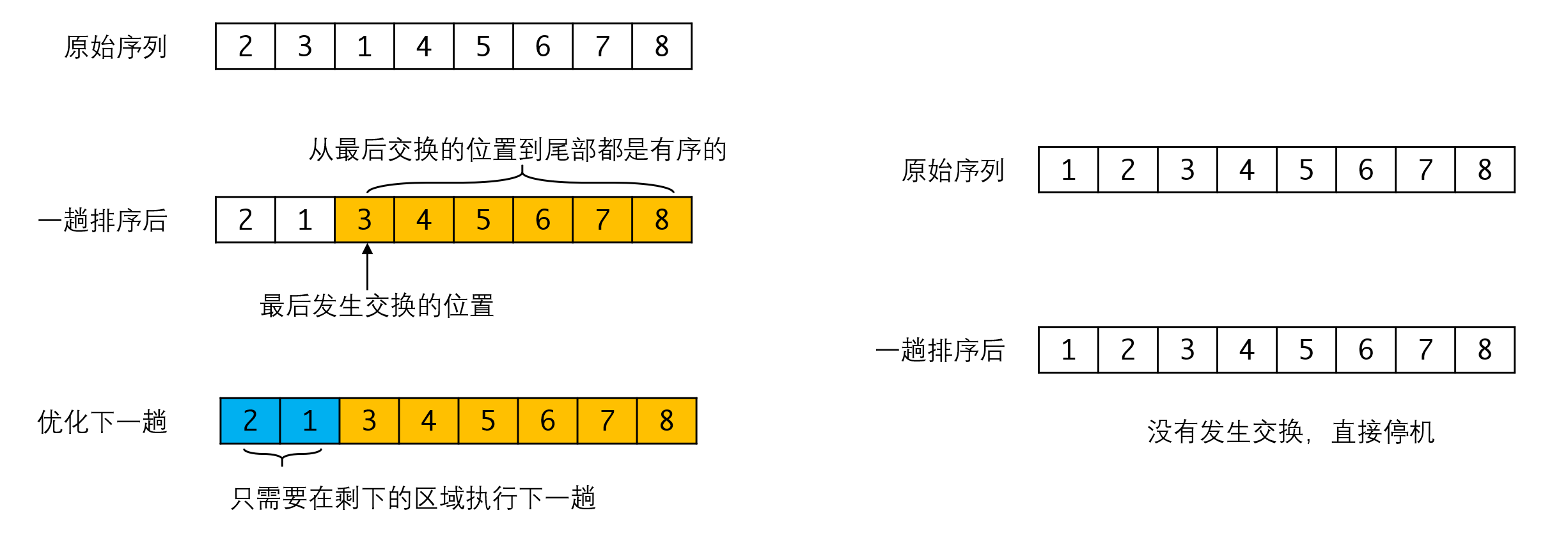
第一趟排序时，最后发生交换的位置是1和3。根据冒泡排序的性质我们可以推断，从3开始到整个序列的最后，都是有序的（否则就会发生交换）。因此下一回合只需要在3前面的区域中进行交换即可。在每趟排序后记下最后交换元素的位置，下一趟排序只需要执行到这个位置前面的一个位置即可。这是冒泡排序可以进行的优化。

更进一步，如果一个序列已经是有序的，那么一趟扫描之后我们会发现没有任何交换发生，此时我们就可以直接停机了。

算法分析

时间复杂度：冒泡排序的平均时间复杂度和选择排序一样是$O(n^2)$，这是非常显而易见的，不再赘述。但看上面有序条件下的排序，我们可以看出，在最好的情况下，他的时间复杂度是$O(n)$。相对选择排序（交换法），冒泡排序会产生很多额外的交换，因此如果交换的开销很大，那么冒泡排序就会变得很不经济。但如果序列不是完全无序，而是几乎有序，那么冒泡排序的优化手段就可以派上用场了，此时他的速度会比选择排序快。

空间复杂度：算法过程中我们只对元素进行交换，并不存在额外的空间开销，所以空间复杂度是$O(1)$。

稳定性：冒泡排序的交换总在相邻的元素之间进行，因此只要我们对相等元素不进行交换，那么他们的相对位置就不会发生变化，因此冒泡排序是稳定的。

适用范围：我们可以注意到，交换始终在相邻的两个元素之间进行，因此我们不需要随机访问，所以冒泡排序即可以适应顺序结构，也可以适应链式结构。和前面选择排序类似的，因为链式结构交换元素不需要进行移动，只需要简单修改指针，冒泡排序在链式结构上的效率会比较高。

直接插入排序

算法描述

直接插入排序和选择排序有一定的相似性。直接插入排序也把序列分为两个部分，一部分是已经排序完成的序列（a[0~i-1]），另一部分是尚未完成排序的序列（a[i~n]），每次我们都把a[i]插入到`a[0~i-1]中合适的位置，使得得到得序列保持有序。重复这一过程直到所有元素都有序：

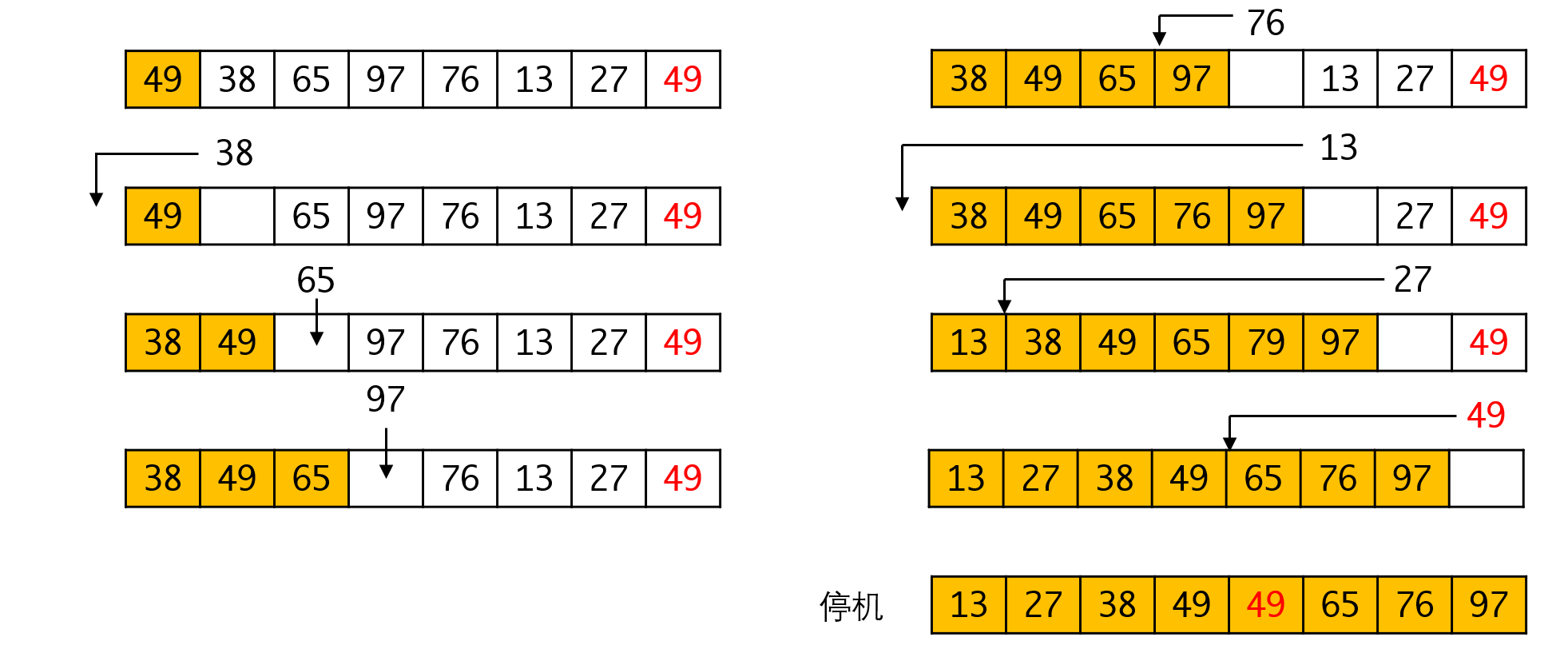
请注意直接插入排序和选择排序的区别，选择排序总是选择剩余序列里最小的那个进行插入，而已经有序的序列是不会再动的。而直接插入排序总选择剩余序列的第一个进行插入，所以已经有序的序列还会不停调整。

直接插入排序的优化

考虑下图中左边的序列：

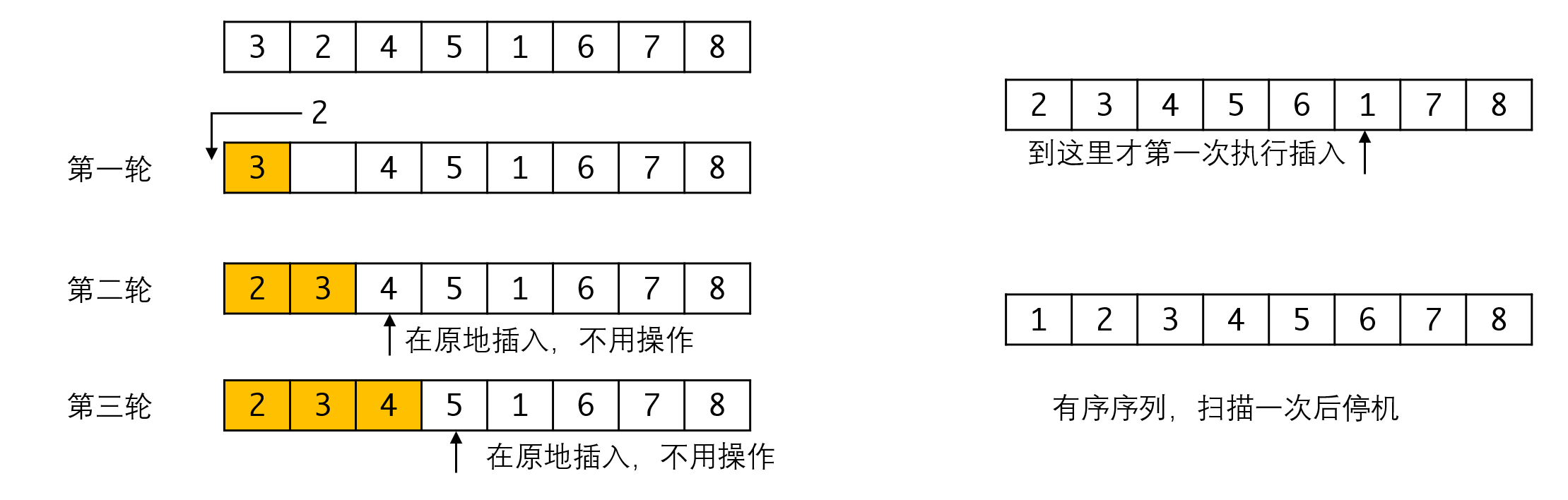
在第一轮之后，后面的4和5都相当于在原位插入，实际上是不需要操作的。所以这两轮相当于轮空了。所以我们可以得出一个结论：只有当a[i]比a[i-1]小的情况下，才需要执行插入，否则本轮可以直接轮空。这就意味着我们每次只需要向后找到第一个满足a[i]<a[i]的对象执行插入即可，中间的所有元素都可以跳过。

比如右边的第一个序列，我们可以一直找到1再执行插入。这意味着前面的4轮我们都轮空了，而之后再从7开始向后找不到满足条件的情况，因此这个序列只需要执行一次插入，进行两趟扫描就可以结束了。

更极端一点的情况，如果序列本身就有序，那么一趟扫描之后，因为找不到任何需要进行插入的情况，一趟扫描之后算法就可以结束了。

直接排序算法的另一种优化手段是寻找插入位置时，因为待插入序列已经有序，我们可以利用二分搜索来进行查找，优化搜索的时间。

算法分析

时间复杂度：直接插入算法每一轮的时间开销主要由两部分：查找插入位置和执行插入。

如果序列是顺序结构，那么查找插入位置我们可以用二分搜索来执行，时间复杂度是$O(logn)$，而插入的时间复杂度我们知道是$O(n)$。所以总体时间复杂度是$O(n)$。

如果序列是链式结构，那么插入的时间复杂度是$O(1)$，但搜索对应插入位置的时间复杂度是$O(n)$，所以总体的时间复杂度也是$O(n)$。

因此每一轮的时间复杂度是$O(n)$，而我们要执行$n$轮，所以平均时间复杂度是$O(n^2)$。

对于最好的情况，也就是序列已经有序的情况，根据上面优化的讨论，我们可以得到此时的时间复杂度是$O(n)$，与冒泡排序算法是一样的。

空间复杂度：直接插入算法的插入过程都在原有的空间上执行，不需要开辟更多的空间，所以空间复杂度是$O(1)$。

稳定性：算法在执行插入时，总是把后面的元素插入前端已经有序的序列。因此只需要保证元素相等时，被插入元素总是插入相等元素的后方，即可以保证两者的相对位置不发生变化。所以直接插入算法的稳定性是有保证的。

适用范围：正如我们前面讨论时间复杂度是讨论的那样，直接插入算法在链表和顺序表中都可以执行。

直接插入排序是一种性能相对比较好的排序算法，他的优化方式非常直观，对于顺序结构还能通过二分搜索进行优化，因此被广泛研究和使用。比如后面的希尔排序，就是对直接插入排序的优化。另外很多算法比如快速排序，在排序序列数目降低到一定范围之后，也会转而采用插入排序来得到较好综合速度效果。

小结

以上的三种算法是比较基础的排序算法。他们的时间复杂度都无法突破$O(n^2)$的限制。他们是稳定的（或者可以通过选择来达到稳定）。他们的空间复杂度都是$O(1)$。冒泡排序和直接插入排序在最好的情况下（都是序列已经有序）的时间复杂度是$O(n)$，选择排序的时间复杂度则一直保持在$O(n^2)$。这三种算法在顺序结构和链式结构上也都能应用。