非比较排序

非比较类排序并不依赖于元素之间的对比，这么说可能不是很好理解，我们看下面具体的例子就非常清楚了。

计数排序

算法思想（理想的计数排序）

先看一个简单的C语言题目，有助于我们理解计数排序的实现方式：

数数

给定一串数字（数目N<=2*10^7），请你给出每个数字出现的次数。数字范围在[0,1000)以内。

你需要给出出现过的数字的出现次数，从小到大依次输出。每一行一个数字。

例如：假设输入是：2 1 5 3 0 2 1 3

你应该输出：

0 1
1 3
2 3
3 2
5 1

这道题非常适合刚学会数组的同学们尝试一下。

解题的思路非常简单，因为题目里数字的范围远小于数字出现的次数，我们只需要分配一个1000个元素的数组a[1000]，读到某个i时，就++a[i]，打印时我们从0开始依次打印就满足题目要求了。

这个代码非常好写，请自行尝试。

而计数排序只需要将输出的过程稍作修改——按顺序向原始空间内输出a[i]个i即可：

计数：

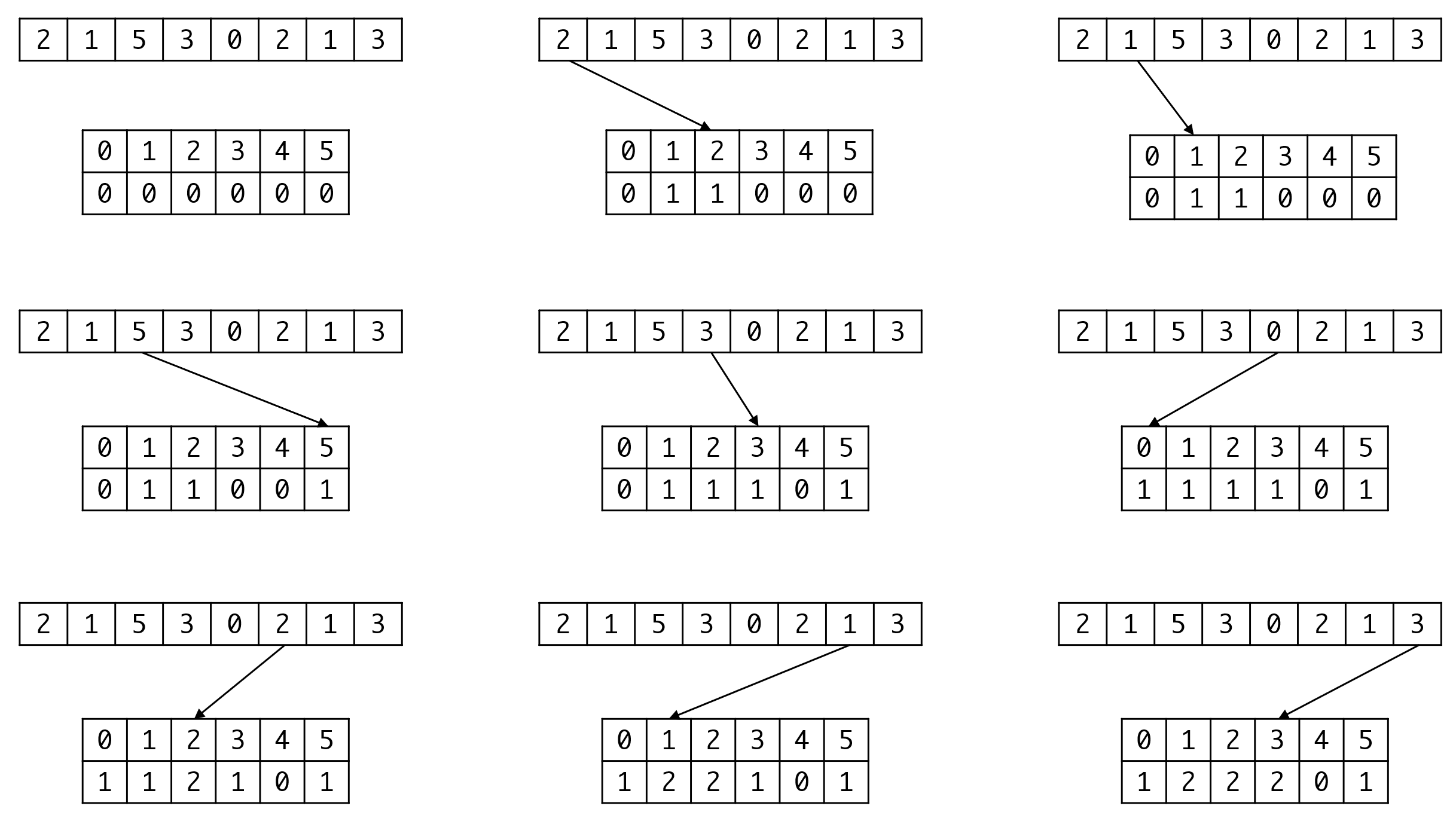
排序：

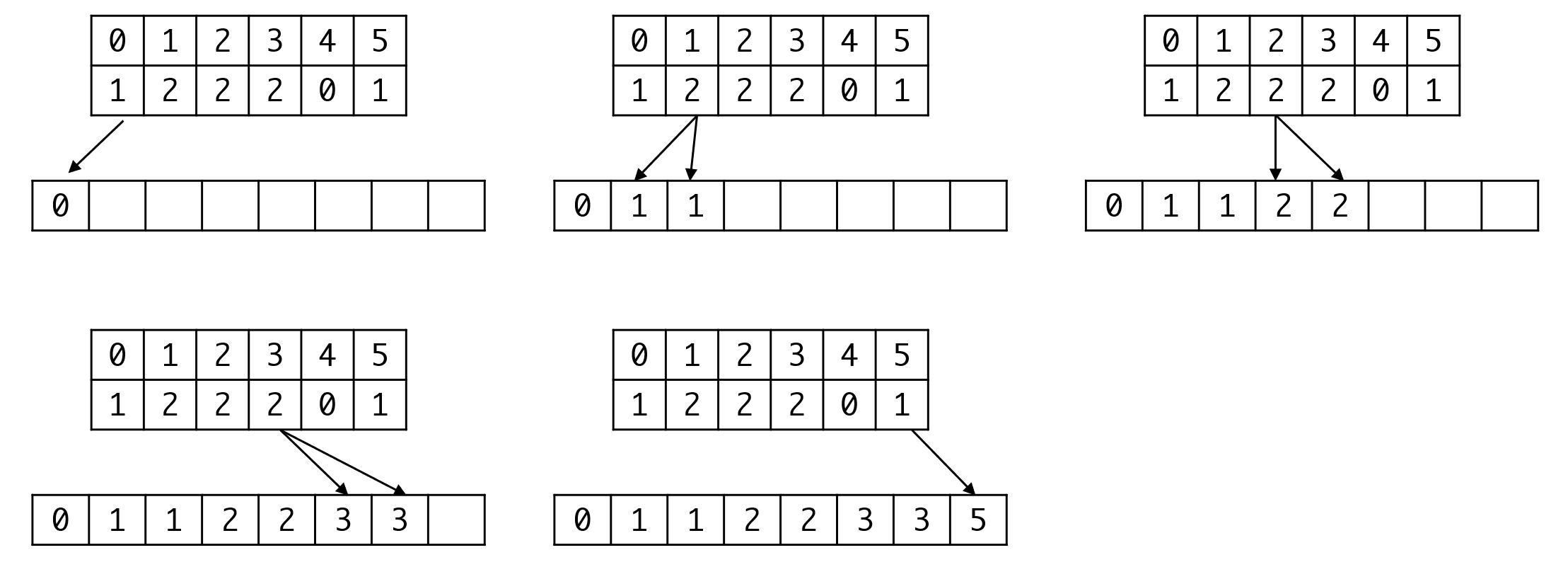
你可能会想：这也算排序？这不人人都会？其实这个算法充分说明了：即便只用基础的知识，一样可以写出非常有效的算法。

实际的计数排序

我们上面讨论的计数排序，是很难应用到实际工作中的，因为我们都知道，排序并不是为了排数字，而是为了根据对象的关键字来对对象进行排序。而当我们执行计数时，我们实际上抹掉了对象，只留下关键字。当我们输出排序结果时，我们无法从排序的关键字里恢复对象，那么整个排序算法也就没意义了。

因此如果要让计数排序可以实用，我们需要做一些处理，我们对计数之后的数组C[k]进行变换，从1开始，令C[i+1]=C[i]+C[i+1]-1。

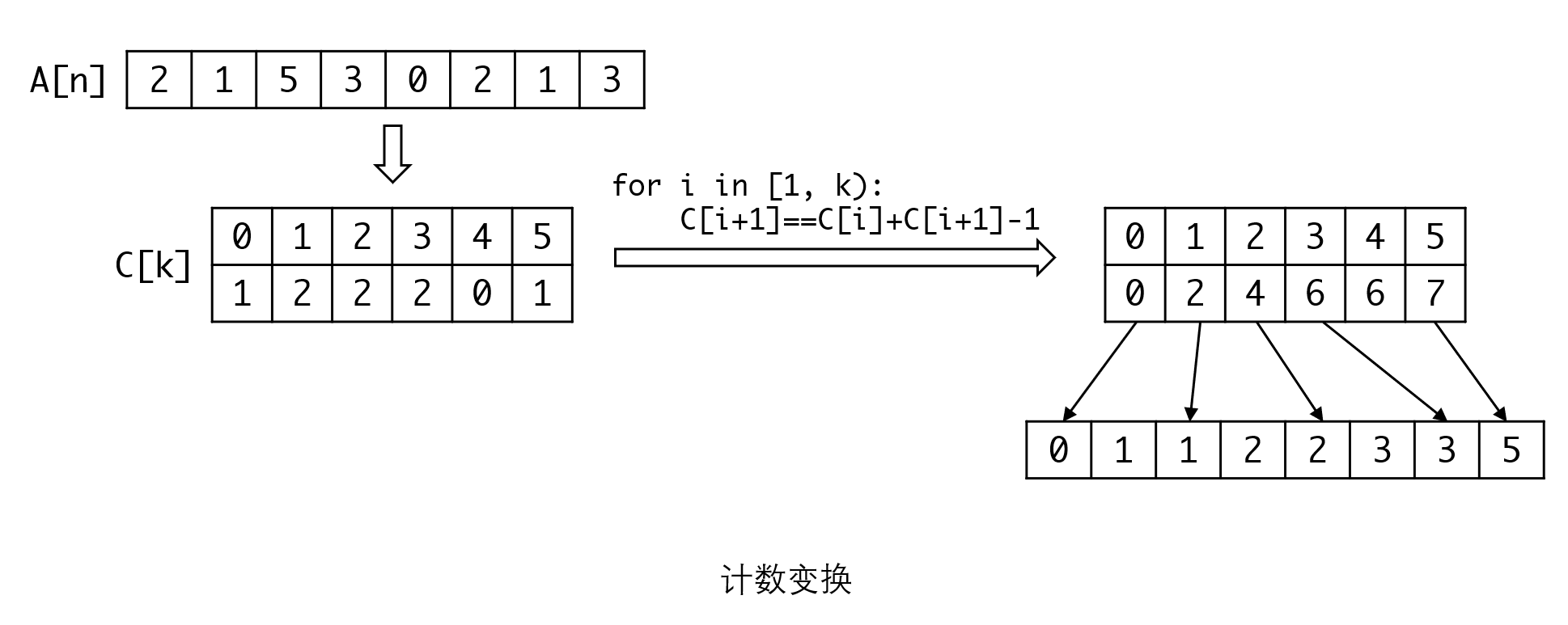
此时我们会发现，计数数组C[k]里的元素，已经变成了对应值的最后一个元素的位置。

接下来的输出就顺理成章了：从后往前遍历数组A[n]，则C[A[i]]即是A[i]这个元素在排好序的数组中的位置。之后我们需要将C[A[i]]--，为下一个相同值的元素做准备。这样说可能有点抽象，我们直接看如何处理。

注意此时我们需要一个额外的空间来存放排序之后的结果，不能复用A[n]，因为可能被覆盖。我们用数组B[n]来存放排序后的结果：

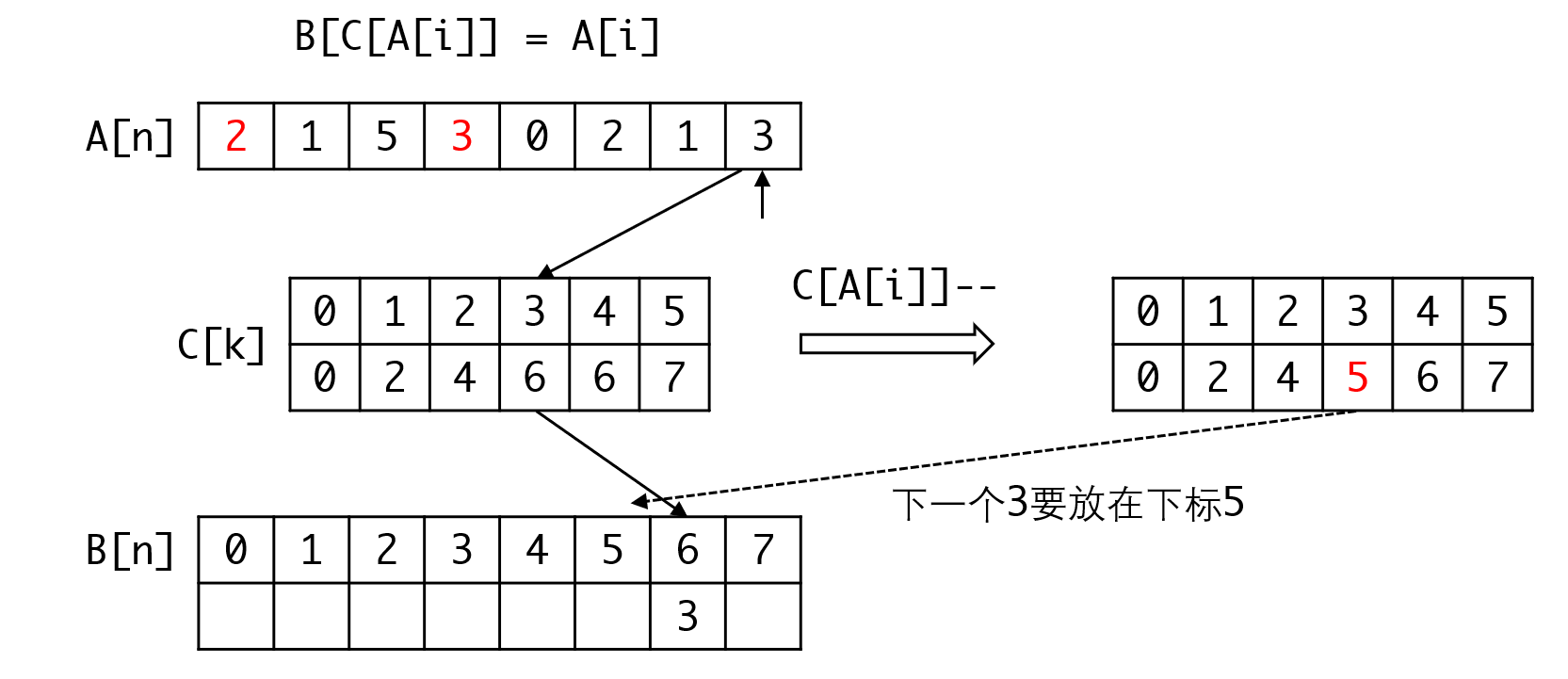
因为C[j]此时表示值为j的元素存放的最后一个下标，因此我们从后往前遍历，对于A[i]，其位置位于新排序后的C[A[i]]处，直接赋值即可。

之后我们还需将C[A[i]]--，使其指向下一个值为A[i]的元素的位置。

我们看一遍完整的处理过程：

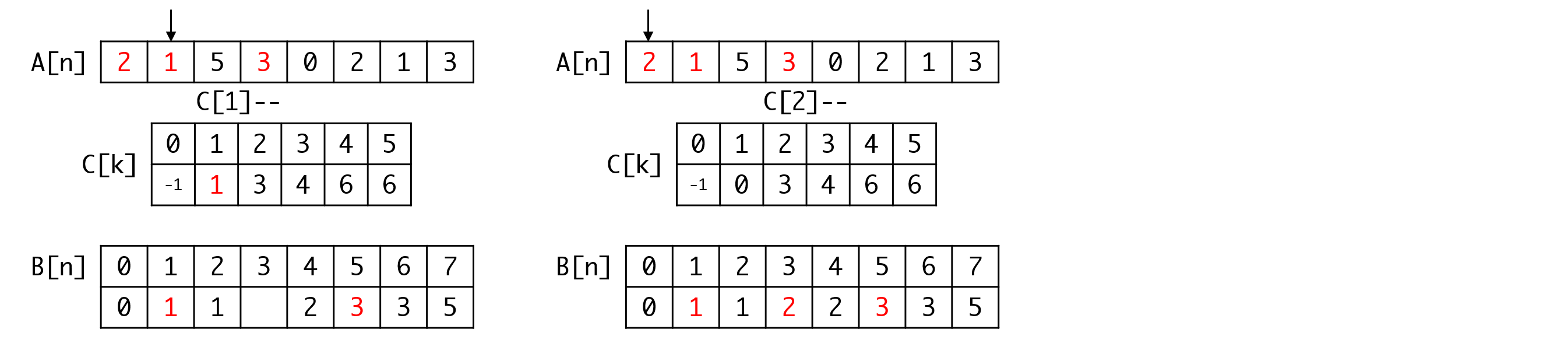
从这里我们也可以看出，用这种方式处理的计数排序是稳定的。

算法分析

计数排序的时间复杂度取决于：数字的数目和数字的范围。我们共遍历两遍A[n]，一次从头到尾，另一次从尾到头。变换C[k]需要遍历C[k]一次，因此时间复杂度是：$O(2n+k)$。

空间复杂度：计数排序需要一个额外的C[k]的空间来进行计数，同时输出空间和源空间不能是同一个空间，所以空间复杂度是$O(n+k)$。

适应性：因为我们需要对结果B[n]执行查表，所以计数排序不能应用于链表。

稳定性：根据上面的结果，显然计数排序是稳定的。

计数排序看上去是一种很美好的排序算法，时间复杂度只有O(n)这个级别，快于所有比较类排序（最快$O(nlogn)$）。但实际上计数排序的限制很大。我们很容易看出计数排序是一种空间换时间的做法。如果k——也就是数字的范围——远小于数字的数目n，那么它确实是非常好的算法。但如果反过来，k比n大得多，那么显然计数排序就不是一种经济的算法。它的空间开销和时间开销都会大幅度上升。

基数排序

算法思想

基数排序是另一种非比较排序，它的空间开销比计数排序小，但相应的复杂度也更高一些。基数排序的基本思想是在基数——你可以简单理解为每个不同的位——上执行排序过程，来达到降低空间开销的作用。

我们看一个具体的过程：

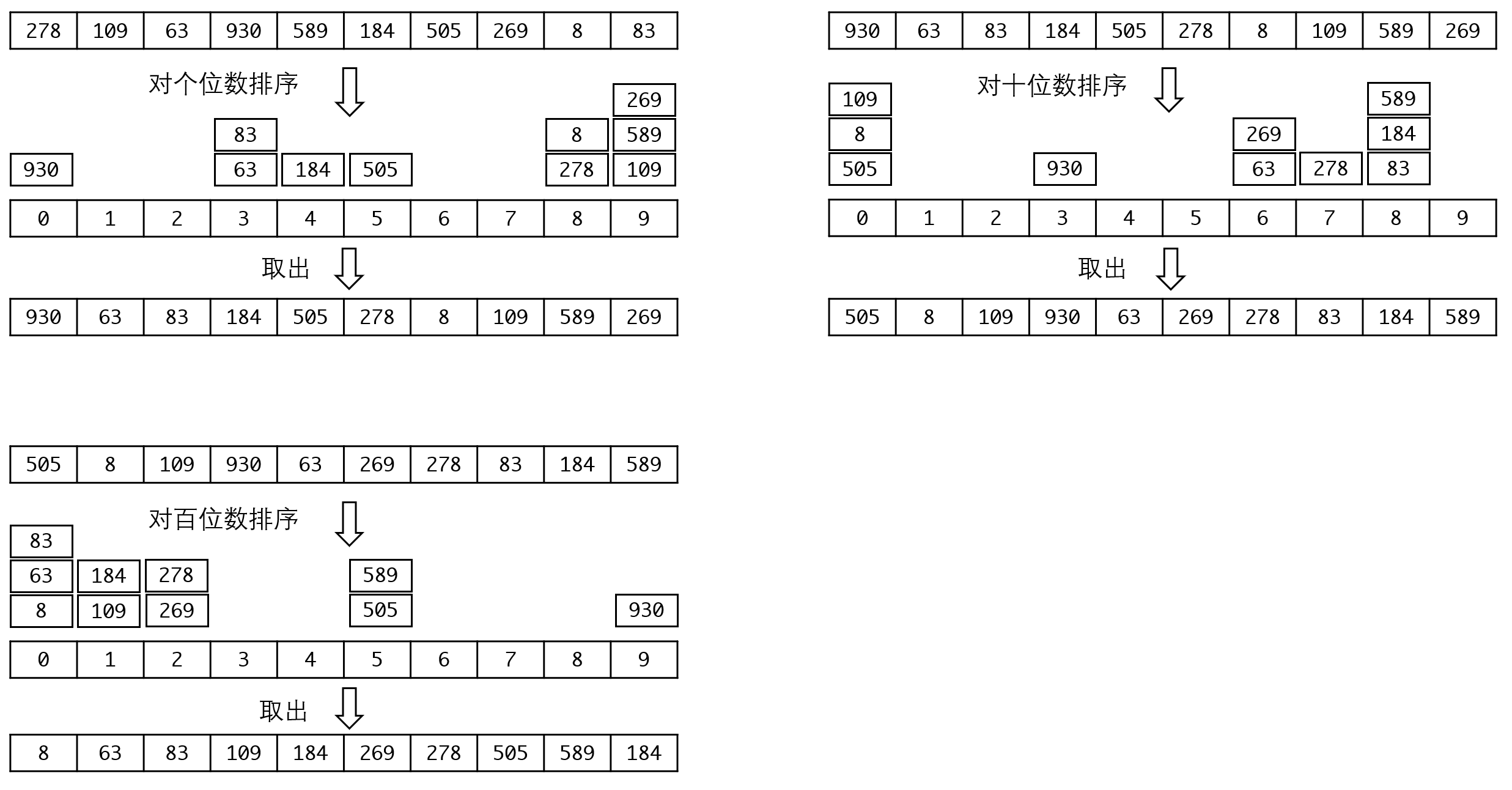
整个过程很容易理解，实在是一种非常巧妙的排序算法。

算法分析

时间复杂度：基数排序需要执行k轮，k由选择的基数和数值的范围决定。每一轮的时间复杂度都是$O(n)$，因此基数排序的时间复杂度是$O(kn)$。

空间复杂度：基数排序需要为中间过程开辟新的空间，每一轮的开销为$O(n)$，空间可以复用，因此空间复杂度为$O(n)$。

稳定性：只要放入每个基底的次序和取出的次序是一致的，那么元素的相对位置就可以得到保证，所以基数排序是稳定的。

适应性：基数排序并不存在跳跃选择的要求，因此可以适用于链表。

可以看出基数排序是比计数排序空间要求更可控、应用范围更广的排序算法。它一定程度上降低了对空间的开销。但它实际上是以时间复杂度的增加为代价的，而且它的中间步骤逻辑较为复杂，需要链表等更为复杂的数据结构。此外它也严重依赖于基数的选取。在数据范围比较大的情况下，它也有和计数排序一样的时间复杂度过高的问题。

总结

本章我们学习了两种常见的非比较排序算法，从中大家可以看出非比较排序和比较排序算法的区别。本质上非比较排序的基本思想都是空间换时间，从而避免$O(nlogn)$级别以上的时间复杂度。但非比较排序的性能（空间和时间上）都很容易受数据分布情况的影响。如果数据比较集中，那么他们的效率要高于比较排序，而如果数据离散程度很高，分布不均匀，那么他们的性能就会受很大影响。