排序

从前面顺序表的相关算法中我们已经知道有序序列对一些算法有很好的加速效果，此外如果一个序列是有序的，我们搜索元素的复杂度可以从$O(n)$降低到$O(logn)$，这其实是一个非常大的优化，设想一下在中国的14亿人里搜索某个人，无序序列可能需要14亿次，而有序序列只需要大约30~31次就够了。

把数据“整”成有序的序列是很多算法的第一步，所以我们非常有必要讨论下排序的算法。

分类

原则上排序算法可以分成内部排序和外部排序，所谓内部排序是指所有运算均在内存中进行，不涉及外存（硬盘）的算法。而外部排序算法是数据可能在内存和外存之间交换的排序算法。本课程内我们只讨论内部排序，下面提到排序时，如果不特别说明，都是指内部排序。

我们可以大致把排序算法分为两类：比较排序和非比较排序。比较排序是通过在元素之间比较大小来达到排序的目的，非比较排序则不（全）依赖这点，通常非比较排序都需要额外的外部空间。

比较排序的分类则有不同的维度，如果按排序的平均时间复杂度来区分的话，可以分为速度比较慢的$O(n^2)$基础组和比较快的高级组（除了希尔排序之外都是$O(nlogn)$）。但如果从排序的原理来区分，又可以分为基于元素交换的交换排序、基于元素插入的插入排序、基于元素选择的选择排序和归并排序这4类。这两种分类方式如下图所示：

而非比较排序我们一般不分类，就是三种，技术排序、桶排序和基数排序。

当然这种分类方式比较简略，也有很多混合式的排序算法，不过大体上他们可以代表排序算法的几种思想。

我们的课程会采用第一种分类方式，有助于大家从浅到深去理解各种排序算法。

算法的评价

之前我们评价算法可以从时间复杂度和空间复杂度两个角度出发。但对于排序算法来说，我们会考虑时间复杂度的最好、最坏和平均的三种情况。此外我们也要考虑排序算法的稳定性。所谓稳定性，是指当两个值相等的元素，如果排序之后可以保证他们的相对位置不会发生变化，我们就说这个算法是稳定的。反之如果无法保证相对位置不发生变化，则称该算法是不稳定的：

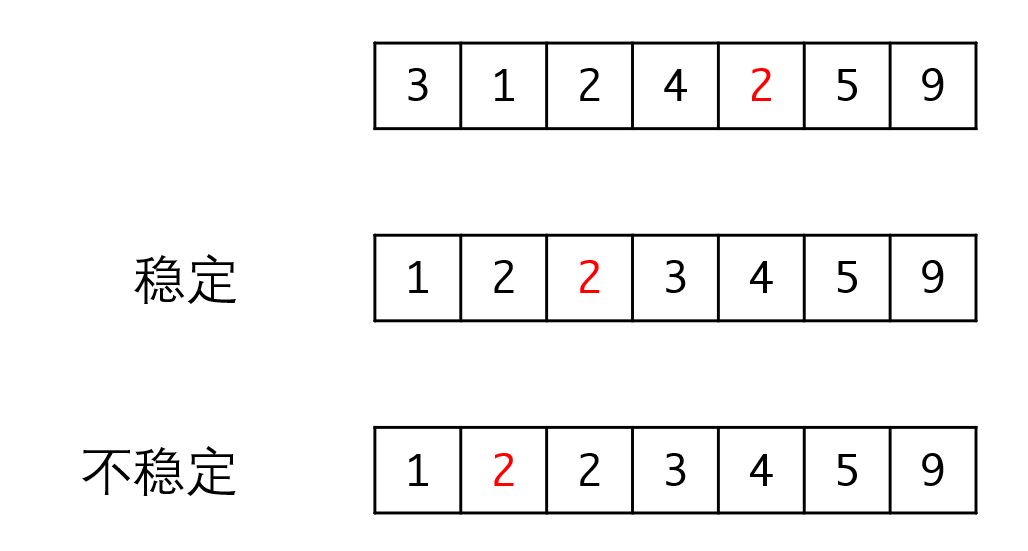
上面的例子里中，有两个2，其中黑色的2排在红色的2之前。如果经过排序之后能够保证黑色的2也同样排在红色的2之前，也即排序的前后两个2的相对位置并没有发生变化，那么算法就是稳定的。

反之如果像下面一样排序之后红色的2有可能排在黑色的2之前，那么这个算法就是不稳定的。

为什么我们需要考查算法的稳定性呢。考虑下面这种要求：我们要求对班级进行排序，优先按年级排，其次按班级排。针对这个需求，如果排序算法是稳定的，我们可以先按班级排，然后再按年级排：

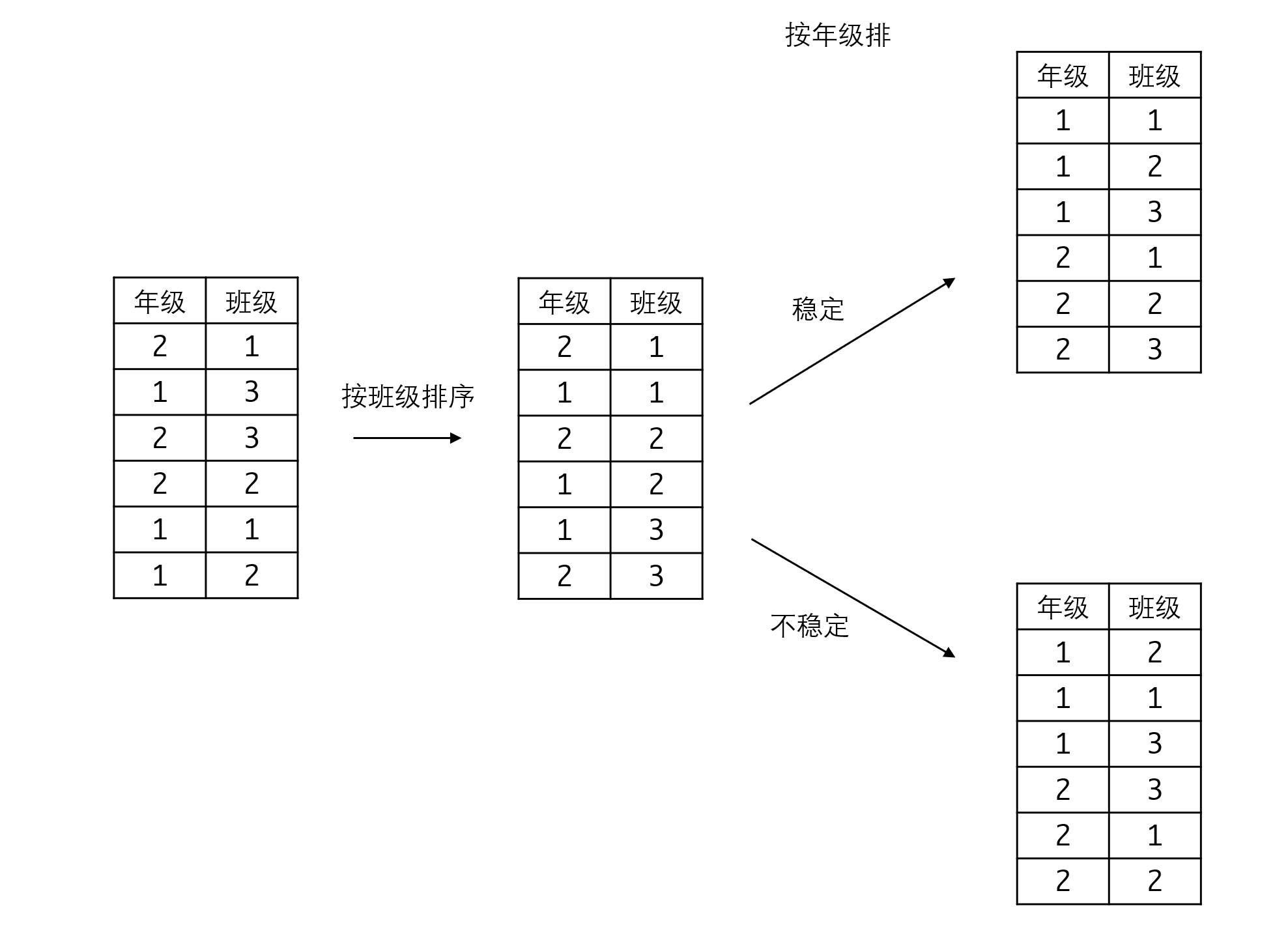
由于稳定的排序算法可以保持相对位置，也就保证了班级的排序结果会被“带入”年级排序的最后结果。反之如果排序算法不稳定，则经过年级排序之后，班级排序的结果无法保存，我们就无法应用这种解法了。

以上是比较常见的算法评价维度，但实际上还有另一个维度是我们可以考虑的，那就是排序的适用范围。我们知道顺序表既可以是顺序结构（顺序表）也可以是链式结构（链表）。那么一个算法是否可以处理这两者，或者只能处理其中一种（通常是只能处理顺序表）也应该是我们考虑的范围。从这个角度去看，会发现很多你觉得没用的算法就有了用武之地。

“最优”排序算法

你可能会有这种想法，为什么我们需要学这么多种排序算法，选一两种最好的排序算法学习不行吗？实际上确实没有所谓的最优排序算法，每一种算法都有其优缺点。即便是一些使用频率比较低的排序算法，例如希尔排序，其思想也有助于我们更好地理解排序算法的需要。

所以这个回答是，不能。